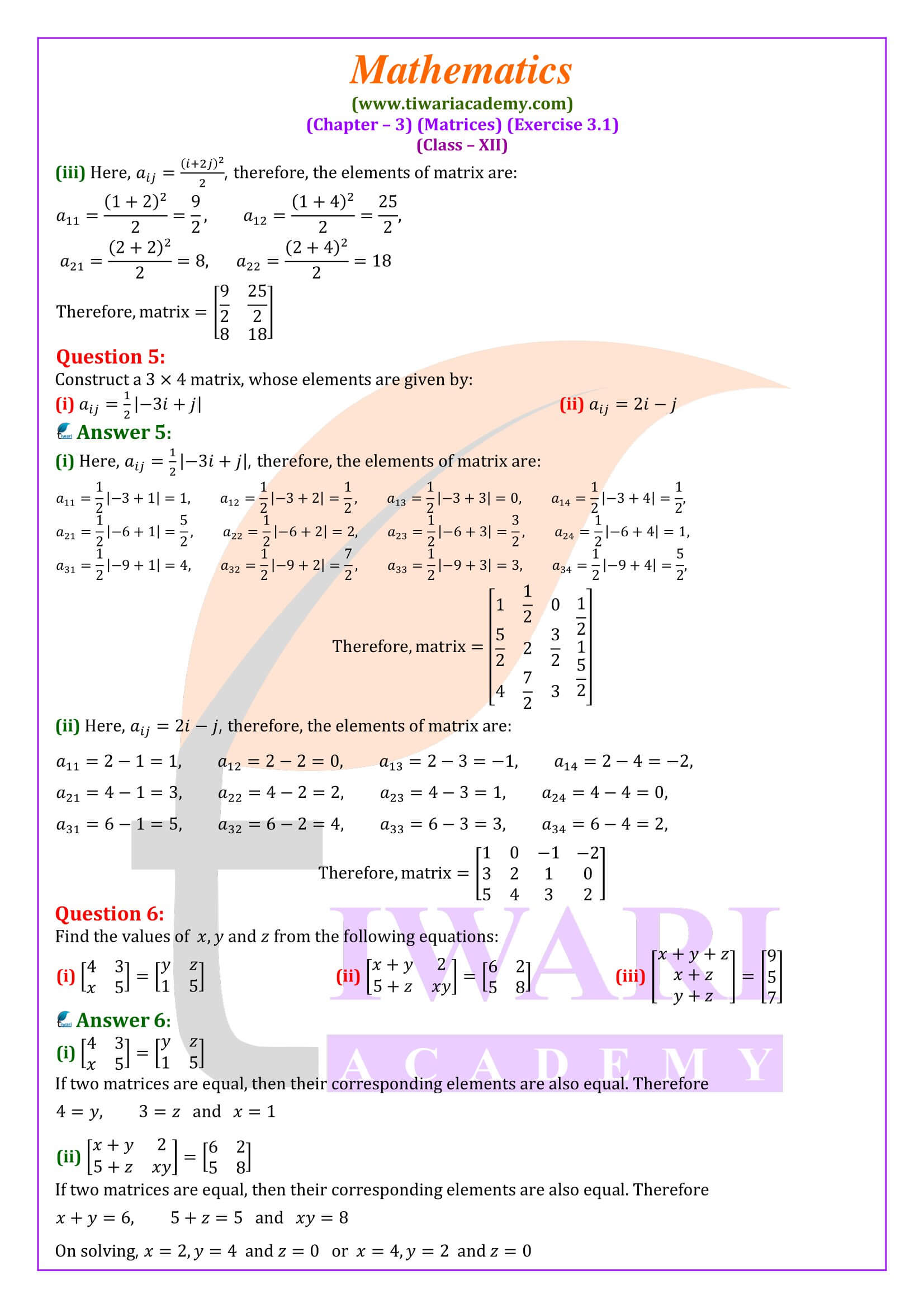
NCERT Solutions for Class 12 Maths Chapter 3 Exercise 3.1 Matrices in Hindi and English Medium modified and updated for academic year 2024-25 exams. The questions of ex. 3.1 class 12th Maths are prepared as per rationalised syllabus for session 2024-25.
Class 12 Maths Exercise 3.1 Solutions in Hindi and English Medium
NCERT Solutions for Class 12 Maths Chapter 3 Exercise 3.1
In UP Board (Uttar Pradesh Maadhyamik Shiksha Parishad) (Intermediate students), are now using NCERT Books for session 2024-25. So, these solutions are important not only for CBSE Board but UP Board, MP Board and board also who are following the latest NCERT Textbooks based on latest CBSE Curriculum. Download (Exercise 3.1) here in PDF file format to use it offline. 12th Maths Chapter 3 Solutions are available in PDF, Online as well as Video format. For the online use contents are given below along with the videos format of solutions. These textbook solutions are applicable for UP Board, MP Board, Gujrat board and all other boards who are using NCERT Textbooks as a course book. For any inconvenience, please call or inform us. We will try to help at our level best.
| Class: 12 | Mathematics |
| Chapter 3: | Exercise 3.1 |
| Topic Name: | Matrices |
| Content: | NCERT Exercise Solutions |
| Content Type: | Text, Images and Videos |
| Medium: | English and Hindi Medium |
12th Maths Exercise 3.1 Solutions
NCERT Solutions for Class 12 Maths Chapter 3 Exercise 3.1 Matrices solutions in English & Hindi Medium are given here updated for new academic session. You can download these solutions form the link given at the page. Get here all the exercises of Class 12 Mathematics Chapter 3 main page. Join the discussion forum to share your knowledge with the others in NIOS Online Admission or CBSE Board concern.
Important Terms About Matrices
- All main diagonal elements of a skew-symmetric matrix are zero.
- Every square matrix can be uniquely expressed as the sum of a symmetric and a skew symmetric matrix.
- All positive integral power of a symmetric are symmetric.
- All odd positive integral power of a skew symmetric matrix are skew symmetric.
Important Questions of 12th Maths Exercise 3.1
What is a Matrix?
A matrix is an ordered rectangular array of numbers or functions. The numbers or functions are called the elements or the entries of the matrix.
What do you understand by order of a Matrix?
A matrix having m rows and n columns is called a matrix of order m × n or simply m × n
matrix (read as an m by n matrix).
If a matrix has 8 elements, what are the possible orders it can have?
We know that if a matrix is of order m × n, it has mn elements.
Thus, to find all possible orders of a matrix with 8 elements, we will find all ordered pairs of natural numbers, whose product is 8.
Thus, all possible ordered pairs are (1, 8), (8, 1), (4, 2), (2, 4)
Hence, possible orders are 1 × 8, 8 ×1, 4 × 2, 2 × 4
What is a column Matrix?
A matrix is said to be a column matrix if it has only one column.
PROPERTIES OF MATRIX ADDITION
- Commutativity: If A and B are two matrices of same order, then A + B = B + A.
- Associativity: If A, B, C are three matrices of same order, then (A + B) + C = A + (B + C).
- Existence of Identity: The null matrix is the identity element for matrix addition. A + O = O + A = A.
- Existence of inverse: For every matrix A = [aij, there exists a matrix – A= [-aij] such that A + (-A) = O = (-A) + A.
- Cancellation laws: If A, B, C are three matrices of the same order, then A + B = A + C implies that B = C and B + A = C + A implies that B = C.
Which main topics will students study in exercise 3.1 of class 12th Maths?
The main topics that students will study in exercise 3.1 of class 12th Maths are:
- 1. Meaning of a matrix.
- 2. Elements or entries of a matrix.
- 3. Order of a matrix.
- 4. Types of matrices (Column matrix, Row matrix, Square matrix, Diagonal matrix, Scalar matrix, Identity matrix, Zero matrix).
- 5. Equality of matrices.
Is exercise 3.1 of grade 12th Maths important for the first term exams?
Yes, from the exam point of view, exercise 3.1 of grade 12th math is important. Questions can come from this exercise in the board exams. All questions and examples of this exercise are important. But the most important examples and questions of this exercise are examples 2, 3, 4, 5, and questions 2, 3, 5, 7, 9, 10.
Which problems of exercise 3.1 of class 12th Maths are of the same type?
In exercise 3.1 of class 12th Maths, there are five examples (examples 1, 2, 3, 4, 5) and ten questions. Example 2 and questions 2, 3 of exercise 3.1 are of the same type. Example 3 and questions 4, 5 of exercise 3.1 are of the same kind. Examples 4, 5, and questions 6, 7, 9 of exercise 3.1 are similar.
How much time, students need to complete exercise 3.1 of class 12th Maths?
Students need a maximum of 2 days to complete exercise 3.1 of class 12th Maths if they give 2 hours per day to this exercise. This exercise is very easy, interesting, and straightforward. Students enjoy doing this exercise. Also, this time depends on student’s working speed and many other factors.