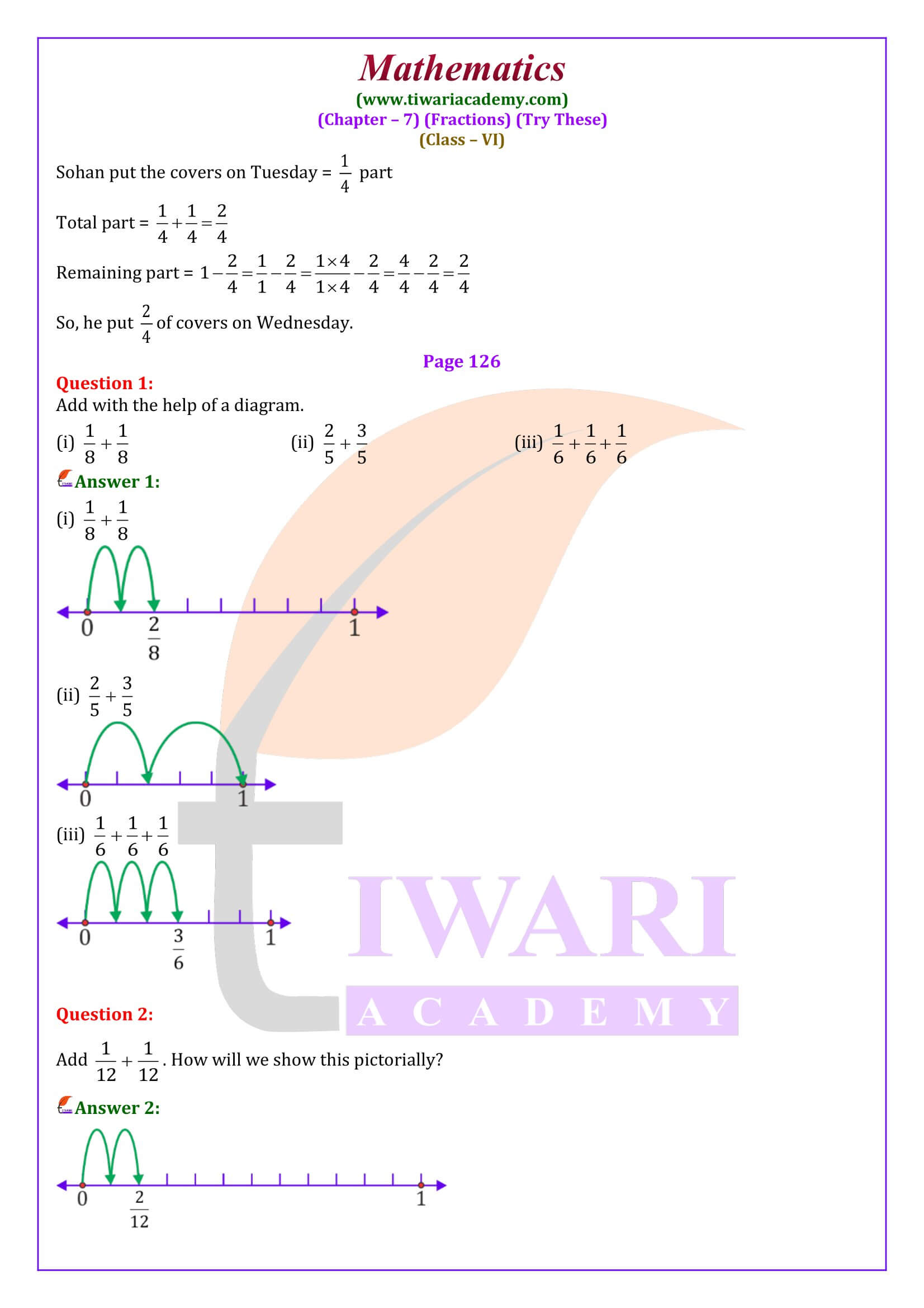
NCERT Solutions for Class 6 Maths Chapter 7 Fractions with Revision Tests and Class 6 Maths Chapter 7 Try These solutions in Hindi and English Medium updated for academic session 2024-25. According to new syllabus and latest NCERT textbook for CBSE 2024-25, there are only six exercises in class 6 Maths chapter 7 Fractions.
6th Maths Chapter 7 Solutions for CBSE and State Boards
Class 6 Maths Chapter 7 Practice Test
6th Maths Chapter 7 Test 1
6th Maths Chapter 7 Test 2
6th Maths Chapter 7 Test 3
6th Maths Chapter 7 Test 4
6th Maths Chapter 7 Test 5
6th Maths Chapter 7 Test 6
6th Maths Chapter 7 Solutions in Hindi Medium
- Class 6 Maths Exercise 7.1 in Hindi
- Class 6 Maths Exercise 7.2 in Hindi
- Class 6 Maths Exercise 7.3 in Hindi
- Class 6 Maths Exercise 7.4 in Hindi
- Class 6 Maths Exercise 7.5 in Hindi
- Class 6 Maths Exercise 7.6 in Hindi
- Class 6 Maths Chapter 7 NCERT Book
- Class 6 Maths Solutions Page
- Class 6 all Subjects Solutions
| Class: 6 | Mathematics |
| Chapter 7: | Fractions |
| Number of Exercises: | 6 (six) |
| Content: | Textbook Exercises Solution |
| Mode of Content: | Text and Videos |
| Session: | CBSE 2024-25 |
| Medium: | Hindi and English Language |
NCERT Solutions for Class 6 Maths Chapter 7
Class VI Mathematics NCERT textbook Exercise 7.1, Exercise 7.2, Exercise 7.3, Exercise 7.4, Exercise 7.5 and Exercise 7.6 in English as well as Hindi Medium updated for CBSE current session. Solutions of Prashnavali 7.1, Prashnavali 7.2, Prashnavali 7.3, Prashnavali 7.4, Prashnavali 7.5 and Prashnavali 7.6 in Hindi Medium PDF file format or View in Video Format free to download. NCERT Solutions for class 6 Science is available to view online as well as downloadable format. Download books from NCERT (https://ncert.nic.in/) official website and solutions from Tiwari Academy to use if offline or continue using online free. Class 6 all subjects CBSE Offline Apps are also available free of cost for Offline use.

Download Class 6 Maths Chapter 7 Solutions in PDF
NCERT Solutions for Class 6 Mathematics Chapter 7 in updated for the new academic session 2024-25 based on new NCERT Books. Contents are made in simplified manner so that a student of standard VI can understand easily. The quality of the contents is also being maintained as the student’s requirement.
Important Questions on Class 6 Maths Chapter 7
What fraction of a day is 8 hours?
Since, 1 day = 24 hours.
Therefore, the fraction of 8 hours = 8/24 = 1/3
What fraction of an hour is 40 minutes?
Since, 1 hour = 60 minutes.
Therefore, the fraction of 40 minutes = 40/60 = 2/3
Kanchan dyes dresses. She had to dye 30 dresses. She has so far finished 20 dresses. What fraction of dresses has she finished?
Total number of dresses = 30
Work finished = 20
Fraction of finished work = 20/30 =2/3
Write the natural numbers from 2 to 12. What fraction of them are prime numbers?
Natural numbers from 2 to 12: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
Prime numbers from 2 to 12: 2, 3, 5, 7, 11
Hence, fraction of prime numbers = 5/11
Write the natural numbers from 102 to 113. What fraction of them are prime numbers?
Natural numbers from 102 to 113: 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113 Prime numbers from 102 to 113: 103, 107, 109, 113
Hence fraction of prime numbers = 4/12 = 1/3
About Class 6 Maths Chapter 7
In 6 Maths Chapter 7 Fractions, we will study the simplification of various fractions as well as the conversion of a fraction into decimal, percentage or any other equivalent. A fraction is a number representing part of a whole. The whole may be a single object or a group of objects.
Let us consider 6/11 is a fraction.
We read it as “Six-elevenths”.
11 is the number of equal parts into which the whole has been divided.
6 is the number of equal parts which have been taken out.
Here 6 is called the numerator and 11 is called the denominator.
Proper fractions. A proper fraction is a number representing part of a whole. In a proper fraction the denominator shows the number of parts into which the whole is divided and the numerator shows the number of parts which have been considered. Therefore, in a proper fraction the numerator is always less than the denominator.
Improper fractions. An improper fraction is a number in which the numerator is always greater than the denominator.
How many illustrations are there in chapter 7 of class 6 Maths?
Chapter 7 of class 6th Maths has 13 illustrations. These illustrations are nice, logical, and interesting. Examples are given before exercises so that students can take the help of examples to solve exercises questions easily.
Which topics do teachers teach under chapter 7 of grade 6 Maths?
Under chapter 7 of grade 6th Maths, teachers teach the following topics:
1. A fraction
2. Fraction on the number line
3. Proper fraction
4. Improper and mixed fraction
5. Equivalent fraction
6. The simplest form of a fraction
7. Like fractions
8. Comparing fractions
9. Comparing like fractions
10. Comparing unlike fractions
11. Addition and subtraction of Fractions
12. Adding or subtracting like fractions
13. Addition and subtraction of unlike fraction
14. The addition and subtraction of mixed fraction
15. Statement questions-Addition and subtraction of fractions.
Is there any chapter for which chapter 7 of class 6th Maths works as a base?
Yes, Chapter 7 of class 6th Maths named “Fractions” works as a base for chapter 2 (Fractions and decimals) of class 7th Maths. Chapter 7 of class 6th Maths is very nice and interesting.
How much time is required to complete chapter 7 of class 6th Maths NCERT?
To complete chapter 7 of class 6th Maths, students required a maximum of 1 week if they give 1-2 hours per day to this chapter. Also, this time increase or decrease according to student’s working speed, efficiency, and capability.