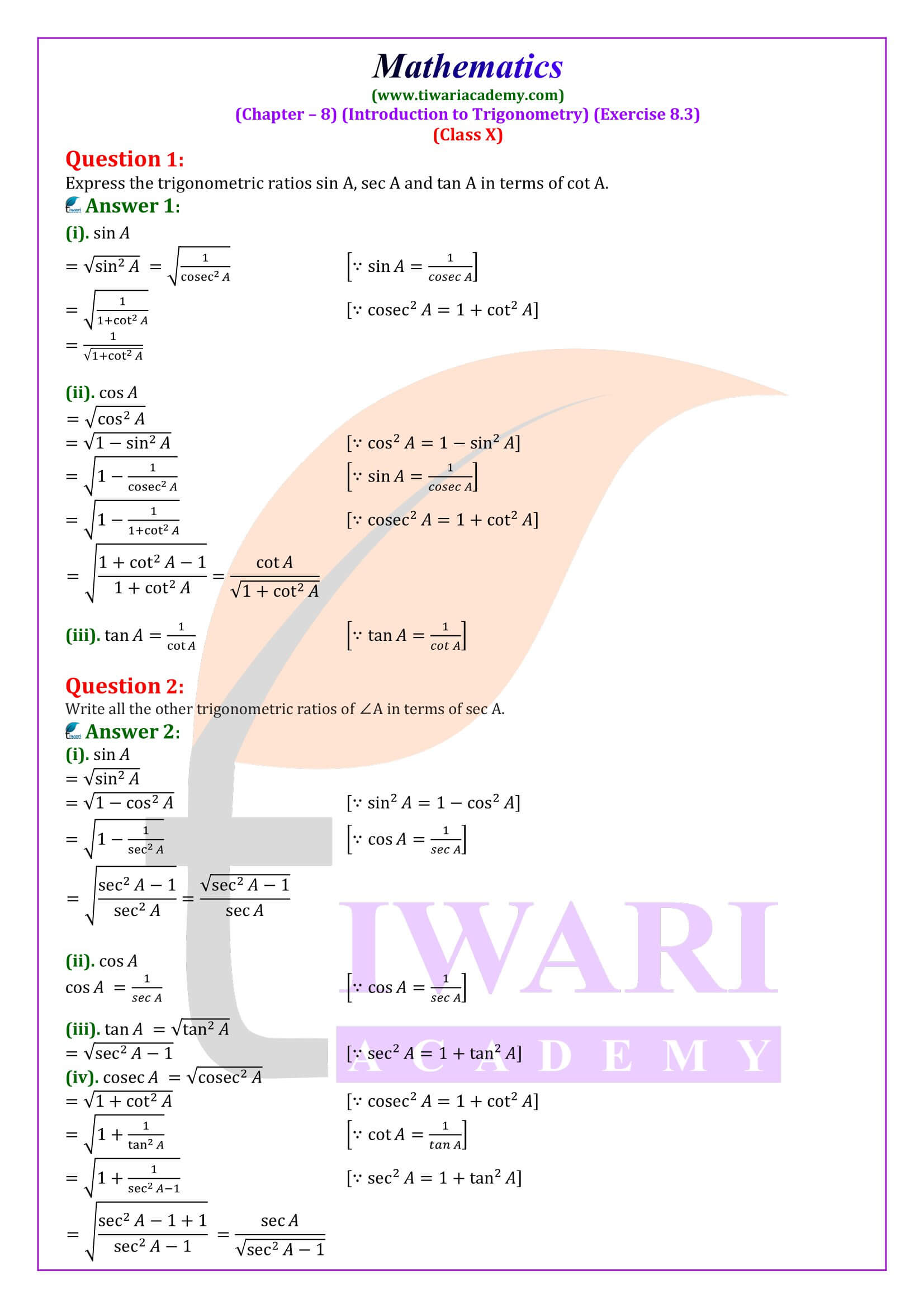
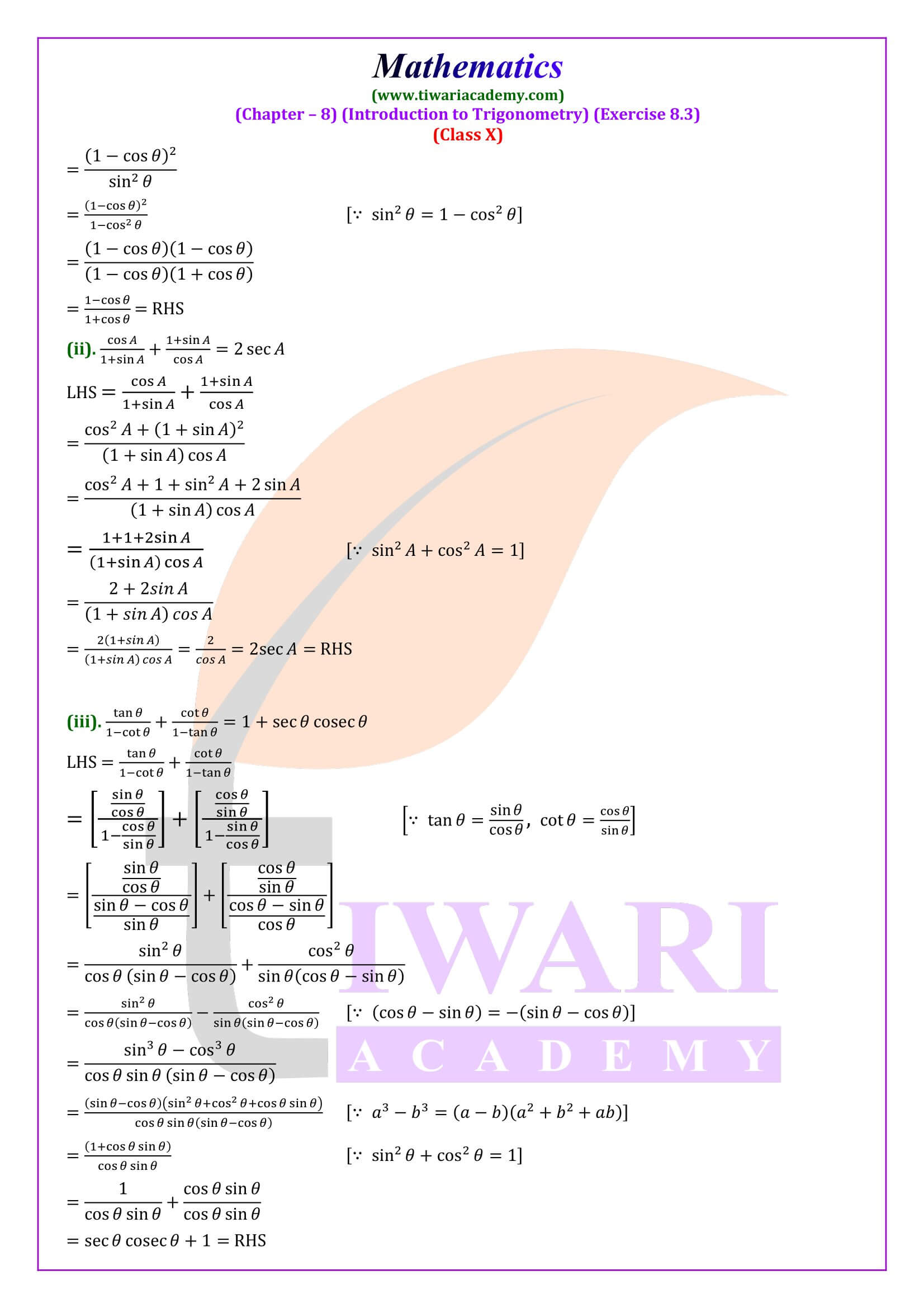
NCERT Solutions for class 10 Maths Chapter 8 Exercise 8.3 Introduction to Trigonometry in Hindi Medium and English Medium updated for CBSE curriculum 2024-25. Class 10 Maths Exercise 8.3 covers the questions based on Trigonometric Identities of sin, cos, tan, sec, cosec and cot.
| Class: 10 | Mathematics |
| Chapter 8: | Exercise 8.3 |
| Topic Name: | Trigonometric Identities |
| Content Type: | Text, PDF, Images and Videos |
| Session: | CBSE 2024-25 |
| Medium | English and Hindi Medium |

NCERT Solutions for class 10 Maths Chapter 8 Exercise 8.3
Class 10 Maths Ex. 8.3 solutions PDF file format to free download updated for new academic year 2024-25 for all students. Download Offline apps based on these solutions or View in Video Format for all board whoever using NCERT Books for their CBSE based exams. Download (Exercise 8.4) in PDF form or CBSE Offline Apps or use the solutions and proof given below as online.
10 Maths Chapter 8 Exercise 8.3 Solutions
NCERT Solutions for class 10 Maths Chapter 8 Exercise 8.3 Introduction to Trigonometry in English Medium as well as Hindi Medium are given below free to use online and liberty to download for offline use. NCERT Solutions Offline Apps with complete description of each questions along with reason of each step are given to free use. All questions are done by the qualified and expert teachers to provide the best for the students. Visit to Class 10 Maths Chapter 8 main page for other exercises whether download or online study.

Important Questions for Proof
- 1. If A, B, C are the angles of triangle ABC then prove that cosec²[(B + C)/2] – tan2(A/2) = 1.
- 2. Prove the following: 2 (sin⁶A + cos⁶A) – 3 (sin⁴A + cos⁴A) + 1 = 0
- 3. Prove that: (1 + cot A + tan A) (sin A – cos A) = sin A tan A – cot A cos A
- 4. If sin θ + cos θ = m and sec θ + cosec θ = n then show that n(m² – 1) = 2m.
Questions from Board Papers
- If time bound and continuity are two measurable quantities respectively equal to A & B. If sin (A – B) = 1/2, cos(A + B) = 1/2, where 0° < A + B ≤ 90° find the values of A and B. [Answer: A = 45, B = 15]
- If x = sin²θ, y = cos²θ, where x & y represents honesty and hard work. (a) What will be the result after joining honesty & hard work? (b) Which mathematical concept has been used here? [Answer: (a) 1, (b) Trigonometry]
Download NCERT Books updated for new session and Offline Apps based on new CBSE Syllabus for Class 10 All subjects. Ask your doubts related to NIOS, UP Board or CBSE Board and share your knowledge with your friends and other users through Discussion Forum.
How many difficult illustrations are there in 10th Maths exercise 8.3?
There are 4 examples (Examples 12, 13, 14 and 15) and 5 questions in exercise 8.3 of class 10th math. Example 12 and Questions 1, 2 are of same type. Example 13, 14, 15 and Question 4, 5 are of same type. Question 3 contains 2 parts, question 4 is choose the correct option type question having 4 parts and question 5 contain 10 parts.
Which is the best ever examples in ex. 8.3 of 10th Maths?
Examples 13, 14, 15 and Questions 4 (all parts) and 5 (all parts) are the most important examples and questions of exercise 8.3 class 10 math because every year questions come from these examples and questions in board exams. These questions and examples have more chance to come in exam.
How long it take to complete exercise 8.3 class 10th mathematics?
Students need maximum 2-3 days to complete exercise 8.3 (chapter 8) of class 10th mathematics if they are giving at least 3 hours per day. This time also depends on student’s speed, efficiency and capability.
How difficult the exercise 8.3 of 10th math is?
Yes, exercise 8.3 of class 10 math is difficult. Many students find question 5 of this exercise the most difficult question because question 5 requires higher order thinking skills. But difficulty level of anything varies from student to student. So, Exercise 8.3 (chapter 8) of class 10th mathematics is difficult or not depends on students also.