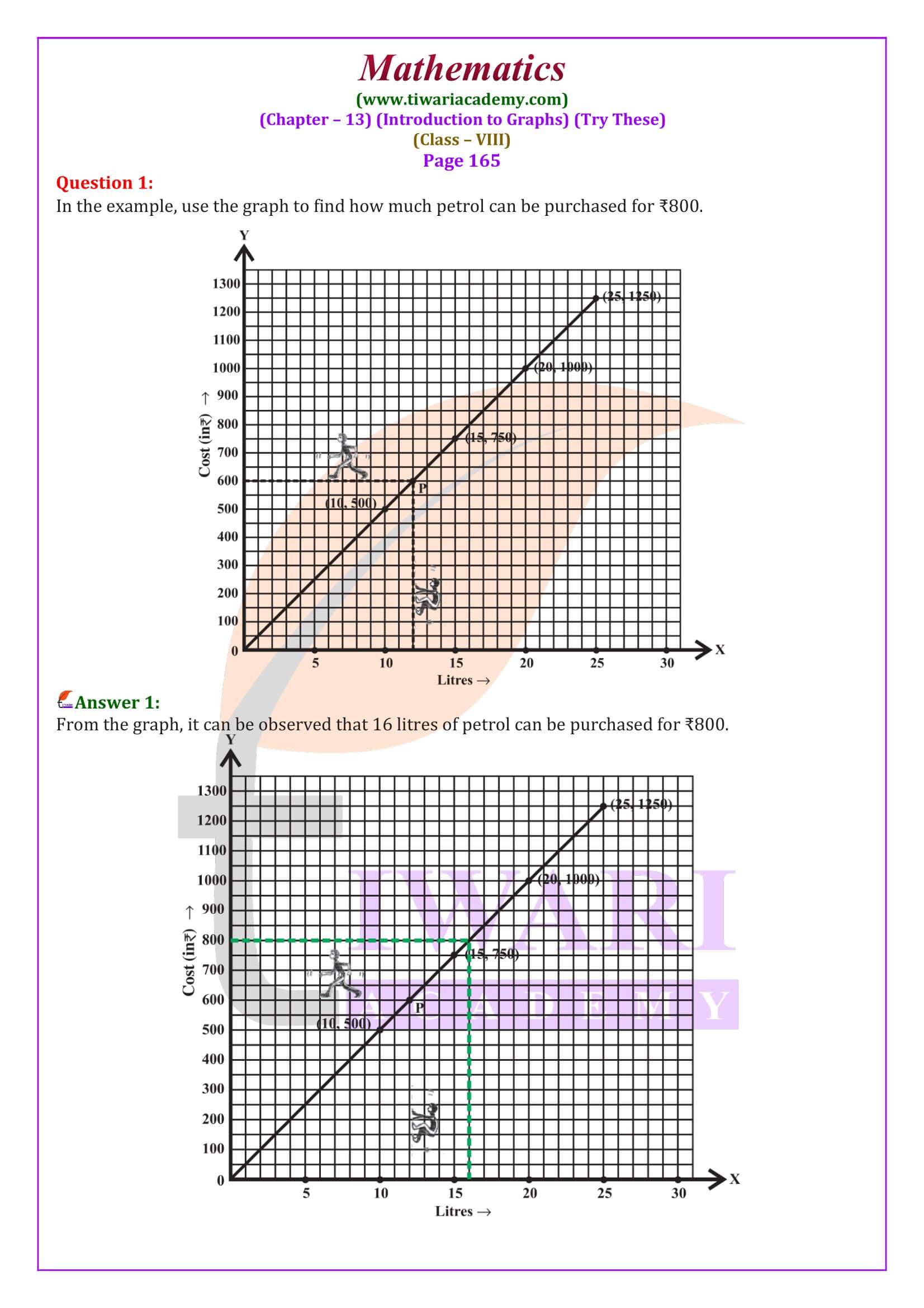
According to new syllabus, there are only two exercises in chapter 13 of 8th mathematics. So, the students studying in grade 8 can get here the NCERT Solutions for Class 8 Maths Chapter 13 and Class 8 Maths Chapter 13 Try These NCERT Solutions Introduction to Graphs in English and Hindi Medium updated for new academic year 2024-25.
8th Maths Chapter 13 Solutions in English Medium
8th Maths Chapter 13 Solutions in Hindi Medium
| Class: 8 | Mathematics |
| Chapter 13: | Introduction to Graphs |
| Number of Exercises: | 2 (Two) |
| Content: | NCERT Exercises Solutions |
| Mode: | Online Text and Videos |
| Academic Year: | Year 2024-25 |
| Medium: | Hindi and English Medium |
NCERT Solutions for Class 8 Maths Chapter 13
Class 8th Maths Solutions are useful for all board who are using NCERT (https://ncert.nic.in/) Books. Download Prashnavali 13.1 and Prashnavali 13.2 in PDF file format free to download or view online without downloading. NCERT Solutions 2024-25 and NCERT Textbooks in English Medium and Hindi Medium for online study as well as PDF format Download to use it offline. Solutions are applicable for all board whoever is following latest CBSE Curriculum 2024-25 for their exams.

Class 8 Maths Chapter 13 Solutions
Class 8 Maths Chapter 13 Introduction to Graphs all exercises in English Medium as well as Hindi Medium are given here to download in PDF format. For any inconvenience regarding website, please call us, we will immediately solve the problem.
In Chapter 13 Introduction to Graphs, we will study various type of graphs like Bar Graphs, Pie Chart, Histogram and line graphs. The concepts of co-ordinate Geometry is also introduced in the later section of this chapter.
Important Terms about Class 8 Maths Chapter 13
State whether True or False. A point whose x coordinate is zero and y-coordinate is non-zero will lie on the y-axis.
True.
State whether True or False. A point whose y coordinate is zero and x-coordinate is 5 will lie on y-axis.
False.
It will lie on axis.

A bar graph is used to show a trend among categories. It may consist of two or more parallel vertical (or horizontal) bars (rectangles) whereas A pie-graph is used to compare parts of a whole. The circle represents the whole. A Histogram is a bar graph that shows data in intervals.
Linear Graphs
To determine the position of a point on a square paper, the coordinates and coordinates must be known. The relationship between an independent variable and a dependent variable is displayed by the equation. It has adjacent bars over the intervals whereas Aline graph displays data that changes continuously over periods of time. A line graph which is a whole unbroken line is called a linear graph. The relation between dependent variable and independent variable is shown through a graph.