on April 15, 2024, 11:48 AM
NCERT Solutions for Class 11 Maths in Hindi and English Medium updated for academic session 2024-25 CBSE and State boards. Get the NCERT Solutions for Class 11 Maths, prepared on revised curriculum 2024-25.
NCERT Solutions of Class 11 Maths
These NCERT Solutions for 11th Maths are freshly updated for the 2024-25 academic year. With the latest NCERT textbooks in mind, students can confidently navigate through all 14 pivotal chapters of 11th-grade mathematics.
Class 11 Maths Syllabus for 2024-25
Chapter 1: Sets
Chapter 2: Relations and Functions
Chapter 3: Trigonometric Functions
Chapter 4: Complex Numbers and Quadratic Equations
Chapter 5: Linear Inequalities
Chapter 6: Permutations and Combinations
Chapter 7: Binomial Theorem
Chapter 8: Sequences and Series
Chapter 9: Straight Lines
Chapter 10: Conic Sections
Chapter 11: Introduction to Three Dimensional Geometry
Chapter 12: Limits and Derivatives
Chapter 13: Statistics
Chapter 14: Probability
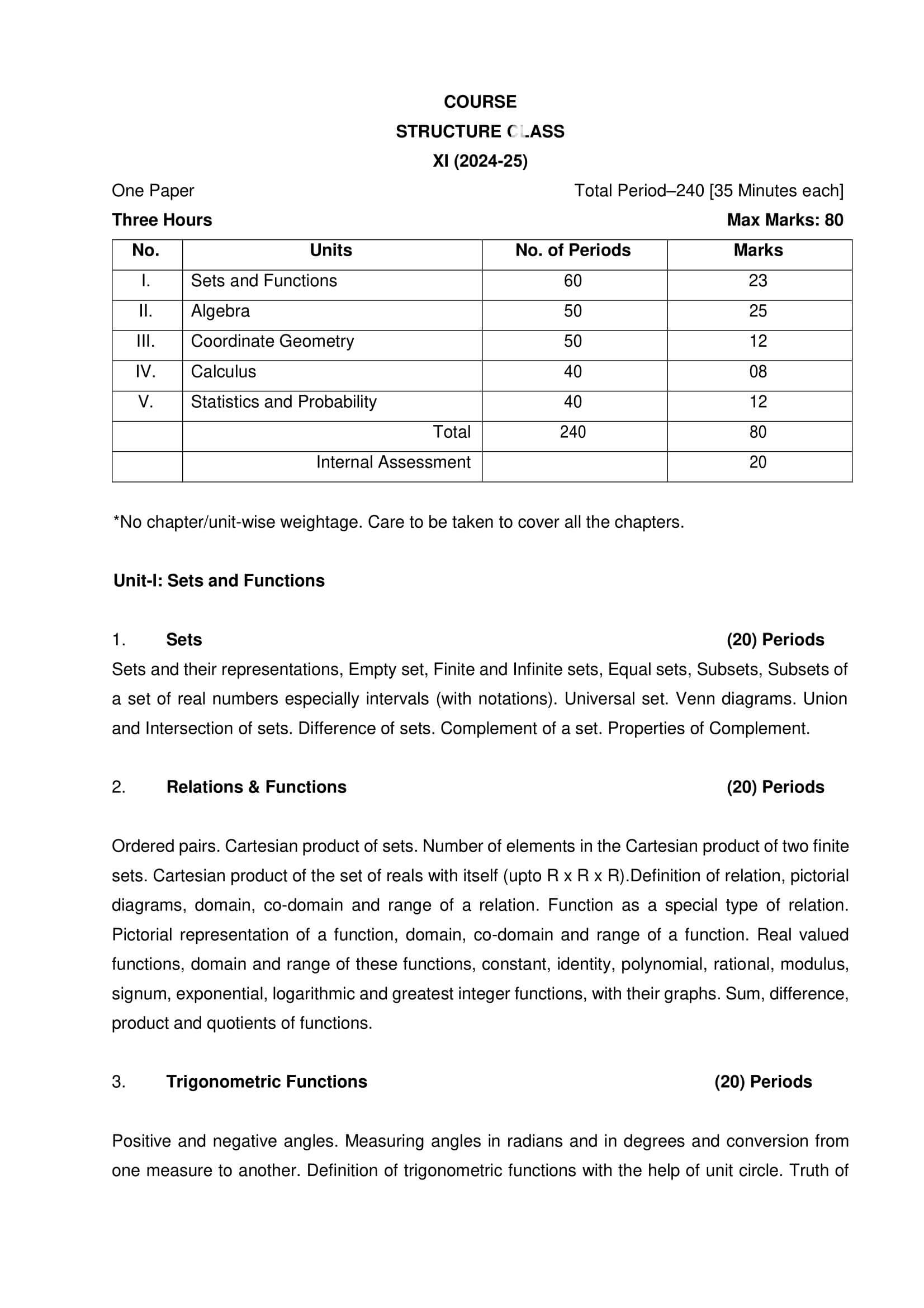
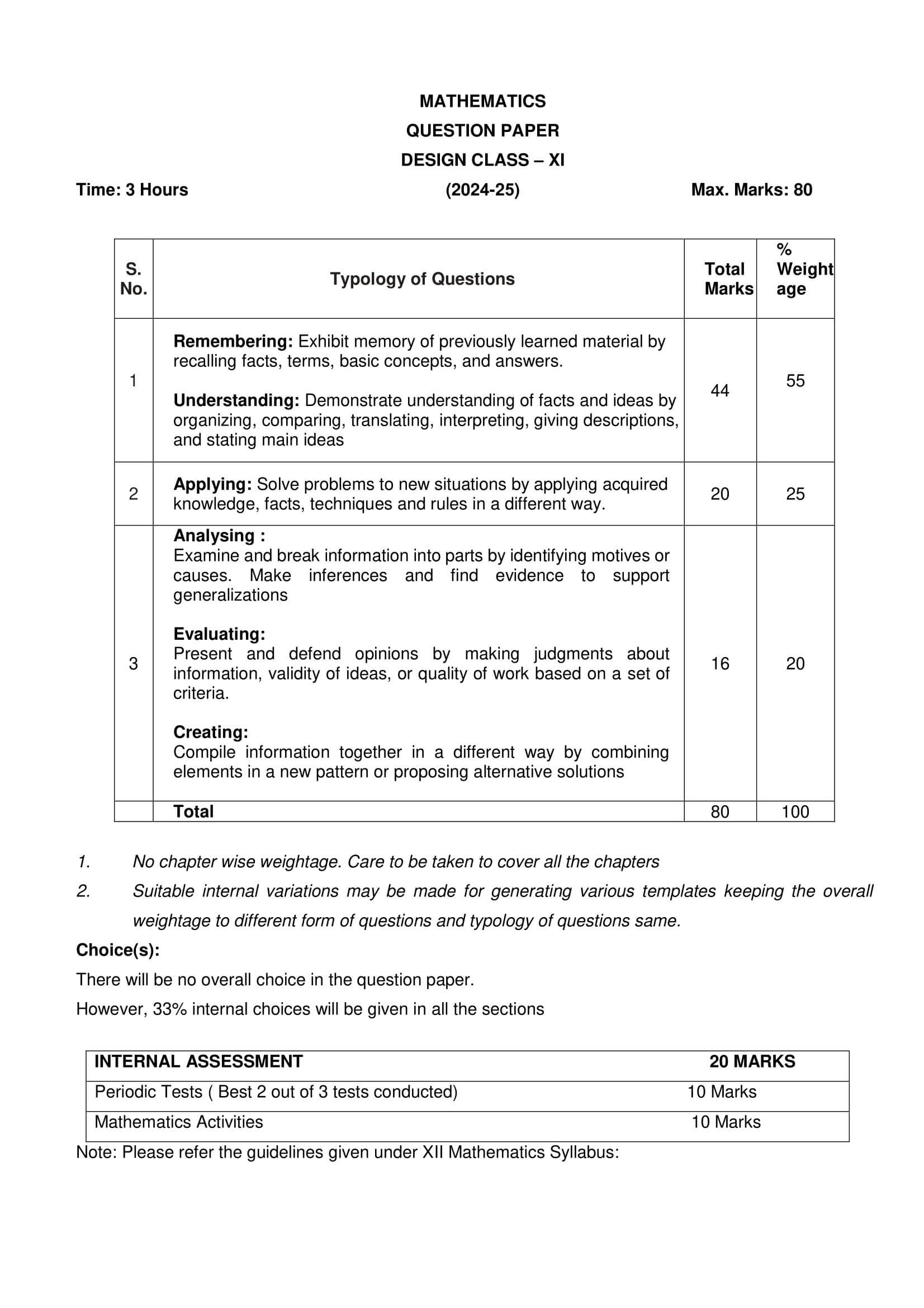
Weightage of Chapters for Class 11 Maths Session 2024-25
| Chapters | Marks |
|---|---|
| 1. Sets, 2. Relations and Functions, 3. Trigonometric Functions | 23 |
| 4. Complex Numbers and Quadratic Equations, 5. Linear Inequalities, 6. Permutations and Combinations, 7. Binomial Theorem, 8. Sequences and Series | 25 |
| 9. Straight Lines, 10. Conic Sections, 11. Introduction to Three Dimensional Geometry | 12 |
| 12. Limits and Derivatives | 08 |
| 13. Statistics, 14. Probability | 12 |
| Periodic Tests ( Best 2 out of 3 tests conducted) | 10 |
| Mathematics Activities | 10 |
| Total | 100 |
Provide us your feedback because your Feedback and Review motivate us to improve the content. NCERT solutions for class 11 Maths are designed to assist students in understanding and solving the exercises and problems presented in the NCERT class 11 mathematics textbook.
Class 11 Apps for iOS and Android
NCERT solutions are widely used by students and teachers in India to prepare for class 11 mathematics exams and build a strong foundation in mathematics. These solutions are available in various formats, including printed books, online PDFs, and digital resources. The NCERT solutions for Class 11 Maths cover a wide range of topics.
Class 11 Maths Solutions in Hindi and English
These NCERT solutions are developed in accordance with the new curriculum 2024-25 prescribed by educational boards in India and are designed to help students understand the concepts, practice problem-solving skills, and prepare effectively for their examinations. The simplified Solutions of Class 11 Maths textbook have been designed to help students.
The NCERT solutions include practice exercises with answers so that students can check their understanding. These CBSE Solutions are prescribed by the National Council of Educational Research and Training – NCERT (https://ncert.nic.in/). In NCERT Maths class 11, there are a total of 14 chapters included in the curriculum 2024-25.
| Class: 11 | Mathematics |
| Number of Chpaters: | 14 (Fourteen) |
| Content: | Solutions and Extra Questions |
| Content Type: | Images, Videos and Text format |
| Academic Year: | Session 2024-25 |
| Medium: | English and Hindi Medium |
Class 11 Solutions App
11th Maths NCERT Solution is the bests study materials for the student who are searching for class 11th Solution Apps for the Academic year 2024-25. Access to Class 11 Maths NCERT solutions can be beneficial for students who are seeking clarity on concepts, practicing problem-solving techniques, or looking for additional resources to enhance their understanding of the subject.
Educational apps offer a wide range of additional resources, such as practice tests, sample papers, and reference materials, to help students excel in their studies. UP Board students also can download UP Board Solution to solve the questions of class 11 Mathematics. It helps students score good marks in their final all exam.
How to Prepare Class 11th Maths for Exams
Start by gaining a comprehensive understanding of the new syllabus for 2024-25. This includes familiarizing yourself with the key topics like Sets and Functions, Algebra, Coordinate Geometry, Calculus, Mathematical Reasoning, Statistics, and Probability.
Regularly review what you’ve learned to reinforce your understanding. Make concise notes or summaries of each topic for quick revisions. Identify your weak areas and focus more on them. Consistent effort and a positive mindset are key to excelling in your Class 11 Maths final exams.
Revised and Updated curriculum 2024-25 for Class 11 Maths
NCERT Solutions for Class 11 Maths All Chapters
You can download Free NCERT Solutions for Class 11 Maths App all Chapters, Exercise-wise in both – Hindi and English medium are given here. Student can also share these Class 11 Maths study materials in PDFs to scholars. Here you also get UP Board Solutions and NCERT Exemplar Class 11 Maths Solutions which give you an idea of exam question pattern. You can score optimum marks with these well-defined Class 11th Maths Solutions.
NCERT Solutions for Class 11 Maths Chapter 1 – Sets
In this NCERT solution for Class 11 Maths Chapter 1, Sets, you came to know a detailed knowledge about Sets along with their representation. Here you get “set” is well defined with its various properties. You can find Chapter Sets Class 11 Maths Solutions in Hindi Medium & English Medium here.
Class 11 Maths Chapter 1 in English Medium
Exercise 1.1 in English
Exercise 1.2 in English
Exercise 1.3 in English
Exercise 1.4 in English
Exercise 1.5 in English
Miscellaneous 1 in English
UP Board and NCERT solutions for class 11 Maths chapter 1 Sets include Empty set, Equal sets, Finite and Infinite Sets, Subsets, Power set and Universal set etc. Students get familiar with the concepts of Union and Intersection of sets which helps students study to draw the Venn diagrams too.
Class 11 Maths Chapter 1 in Hindi Medium
Exercise 1.1 in Hindi
Exercise 1.2 in Hindi
Exercise 1.3 in Hindi
Exercise 1.4 in Hindi
Exercise 1.5 in Hindi
Miscellaneous 1 in Hindi
NCERT Solutions for Class 11 Maths Chapter 2 – Relations & Functions
This Class 11 Maths NCERT Solutions Chapter 2 – Relations & Functions provides you Exercise-wise solution covering all problem sums as prescribed latest CBSE Textbook. All NCERT Solutions for class 11 math chapter 2 Relations & Functions are based on the 12th Class Maths Book Solution.
Class 11 Maths Chapter 2 in English Medium
Exercise 2.1 in English
Exercise 2.2 in English
Exercise 2.3 in English
Miscellaneous 2 in English
Class 11 Maths Chapter 2 in Hindi Medium
Exercise 2.1 in Hindi
Exercise 2.2 in Hindi
Exercise 2.3 in Hindi
Miscellaneous 2 in Hindi
NCERT Solutions for Class 11 Maths Chapter 3 – Trigonometric Functions
NCERT Solutions for class 11 Maths chapter 3 covers positive and negative angles discussion, method of measuring angles in radians. NCERT solutions for class 11 math chapter 3 Trigonometric Functions also covers degrees and conversion from one measure to another as well as.
Class 11 Maths Chapter 3 in English Medium
Exercise 3.1 in English
Exercise 3.2 in English
Exercise 3.3 in English
Miscellaneous 3 in English
Class 11 Maths Chapter 3 in Hindi Medium
Exercise 3.1 in Hindi
Exercise 3.2 in Hindi
Exercise 3.3 in Hindi
Miscellaneous 3 in Hindi
NCERT Solutions for Class 11 Maths Chapter 4 – Complex Numbers and Quadratic Equations
NCERT Solutions for class 11 Maths chapter 4 Complex Numbers and Quadratic Equations with all exercise are well solved by the expert Mathematics teacher. Once you understand the concept properly, then you can proceed with all exercises easily.
Class 11 Maths Chapter 4 in English Medium
Exercise 4.1 in English
Miscellaneous 4 in English
Class 11 Maths Chapter 4 in Hindi Medium
Exercise 4.1 in Hindi
Miscellaneous 4 in Hindi
The Chapter 4 provides details about the algebraic properties of complex numbers. Students learn and practice for both Chapter Complex Numbers and Quadratic Equations class 11 math solutions in Hindi medium and English medium.
NCERT Solutions for Class 11 Maths Chapter 5 – Linear Inequalities
Find NCERT Solutions for class 11 Maths chapter 5 Linear Inequalities with all exercises. Here you came to know about the concept of Linear Inequalities as the name suggests.
Class 11 Maths Chapter 5 in English Medium
Exercise 5.1 in English
Miscellaneous 5 in English
Class 11 Maths Chapter 5 in Hindi Medium
Exercise 5.1 in Hindi
Miscellaneous 5 in Hindi
NCERT Solutions for Class 11 Maths Chapter 6 – Permutations and Combinations
Students get the Free NCERT Solutions for Class 11 Maths Chapter 6 Permutations and Combinations with all exercises here. Chapter 6 covers the Fundamental principle of counting, factorial, derivation of formulae and with its applications permutations, combinations.
Class 11 Maths Chapter 6 in English Medium
Exercise 6.1 in English
Exercise 6.2 in English
Exercise 6.3 in English
Exercise 6.4 in English
Miscellaneous 6 in English
Class 11 Maths Chapter 6 in Hindi Medium
Exercise 6.1 in Hindi
Exercise 6.2 in Hindi
Exercise 6.3 in Hindi
Exercise 6.4 in Hindi
Miscellaneous 6 in Hindi
NCERT Solutions for Class 11 Maths Chapter 7 – Binomial Theorem
NCERT Solutions for Class 11 Maths Chapter 7 Binomial Theorem with all exercise sums are explained and solved by the math teacher having many years of experiences in this subject Maths.
Class 11 Maths Chapter 7 in English Medium
Exercise 7.1 in English
Miscellaneous 7 in English
Class 11 Maths Chapter 7 in Hindi Medium
Exercise 7.1 in Hindi
Miscellaneous 7 in Hindi
NCERT Solutions for Class 11 Maths Chapter 8 – Sequences and Series
This Free NCERT Solutions for Class 11 Maths Chapter 8 Sequences and Series for all exercises are very helpful for the student Class 11. There are three exercises in the total present in chapter 8 which based on 11th Class Maths Book Solution.
Class 11 Maths Chapter 8 in English Medium
Exercise 8.1 in English
Exercise 8.2 in English
Miscellaneous 8 in English
Class 11 Maths Chapter 8 in Hindi Medium
Exercise 8.1 in Hindi
Exercise 8.2 in Hindi
Miscellaneous 8 in Hindi
Download and share NCERT Solutions for Class 11 Maths PDF to your friends and classmates. Get the Sequences and Series Solutions in Hindi and English medium.
NCERT Solutions for Class 11 Maths Chapter 9 – Straight Lines
NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines helps the students to remind the previous class two-dimensional geometry chapter. Shifting of origin, numerous forms of equations of a line parallel to the axis, angle between two lines the slope of a line and, point-slope form, slope intercept form, two-point form, intercept etc.
Class 11 Maths Chapter 9 in English Medium
Exercise 9.1 in English
Exercise 9.2 in English
Exercise 9.3 in English
Miscellaneous 9 in English
Class 11 Maths Chapter 9 in Hindi Medium
Exercise 9.1 in Hindi
Exercise 9.2 in Hindi
Exercise 9.3 in Hindi
Miscellaneous 9 in Hindi
NCERT Solutions for Class 11 Maths Chapter 10 – Conic Sections
This Free NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections provides you with the concept of Conic Sections in detail. There are four exercises in the total present in this chapter which are based on 11th Class Maths Book Solution.
Class 11 Maths Chapter 10 in English Medium
Exercise 10.1 in English
Exercise 10.2 in English
Exercise 10.3 in English
Exercise 10.4 in English
Miscellaneous 10 in English
Class 11 Maths Chapter 10 in Hindi Medium
Exercise 10.1 in Hindi
Exercise 10.2 in Hindi
Exercise 10.3 in Hindi
Exercise 10.4 in Hindi
Miscellaneous 10 in Hindi
NCERT Solutions for Class 11 Maths Chapter 11 – Introduction to Three-dimensional Geometry
NCERT Solutions for Class 11 Maths Chapter 11 Introduction to Three dimensional Geometry is an important chapter. Here you can get Free Exercise-wise solutions present in the NCERT Solutions for Class 11 Maths Chapter 11.
Class 11 Maths Chapter 11 in English Medium
Exercise 11.1 in English
Exercise 11.2 in English
Miscellaneous 11 in English
Class 11 Maths Chapter 11 in Hindi Medium
Exercise 11.1 in Hindi
Exercise 11.2 in Hindi
Miscellaneous 11 in Hindi
Exercise-wise Class 11 Maths NCERT Solutions Chapter 12 – Limits and Derivatives
Here in this Class 11 Maths NCERT Solutions Chapter 12 – Limits and Derivatives, you learn about Calculus which is a Maths dealing with the study of change in the value of a function and points in the domain change.
Class 11 Maths Chapter 12 in English Medium
Exercise 12.1 in English
Exercise 12.2 in English
Miscellaneous 12 in English
Class 11 Maths Chapter 12 in Hindi Medium
Exercise 12.1 in Hindi
Exercise 12.2 in Hindi
Miscellaneous 12 in Hindi
NCERT Solutions for Class 11 Maths Chapter 13- Statistics
Statistics deals with the data collected for specific purposes. This NCERT Solutions for Class 11 Maths Chapter 13 Statistics provide you with some of the important measures of dispersion. There are three exercises in the NCERT Solutions for Class 11 Maths Chapter 13.
Class 11 Maths Chapter 13 in English Medium
Exercise 13.1 in English
Exercise 13.2 in English
Miscellaneous 13 in English
Class 11 Maths Chapter 13 in Hindi Medium
Exercise 13.1 in Hindi
Exercise 13.2 in Hindi
Miscellaneous 13 in Hindi
NCERT Solutions for Class 11 Maths Chapter 14 – Probability
NCERT Solutions for Class 11 Maths Chapter 14 Probability is well defined with step by step solutions so that students can easily understand the concept. Here you can get the idea of the concept of probability properly.
Class 11 Maths Chapter 14 in English Medium
Exercise 14.1 in English
Exercise 14.2 in English
Miscellaneous 14 in English
Class 11 Maths Chapter 14 in Hindi Medium
Exercise 14.1 in Hindi
Exercise 14.2 in Hindi
Miscellaneous 14 in Hindi
We at Tiwari Academy helps all students to discover better ways to solve math problem sums by using their logical skills. By the help of these NCERT Solutions for Class 11 Maths All Chapters, exercise-wise can be a good move towards the Mathematics world and achieve greater success not only in final exam but also it helps you in higher classes as well.
Importance of Learn NCERT Solutions for Class 11 Maths from Tiwari Academy
There are many Advantages of Learn Class 11 Maths NCERT Solutions from Tiwari Academy. You can experience an immense understanding of the overall concept of all the given chapters in NCERT, (National Council of Educational Research and Training) books.
The main Advantages of Learn Class 11 Maths NCERT Solutions from Tiwari Academy are:
Better Understanding of the Concepts
NCERT Solutions for Class 11 Maths All Chapters of the Tiwari Academy contain easy yet comprehensive explanations. All solutions are solved by the experienced Math Teacher keep in mind better understanding of the concepts.
Faster Learning Process
We at Tiwari Academy provides all solutions in both modes Hindi and English you can easily grasp basic concepts better and faster. You get to learn concepts much faster and also learn quickly.
Easy Method to Understand
All Maths solutions are well designed in an easy step by step method so that student can easily understand all exercise sums. Students can clear all the concepts and logic of each sum.
Solutions in PDF File
All NCERT Solutions for Class 11 Maths All Chapters, Exercise at Tiwari Academy are available in easy PDF format so that you can download it and learn it when you want to learn or while offline.
Completely Free of Cost
All the NCERT Chapter-wise solutions are available here with FREE of Cost. You no need to pay anything here, and also there is no need for any login and registration.
Based on Latest CBSE Curriculum 2024-25
All solutions are based on updated CBSE Syllabus and cover all questions as on the NCERT Textbooks.
How are CBSE 11 Maths Solutions of NCERT Helpful for Final Exams?
CBSE Class 11 Maths is an important subject for students. As the syllabus of CBSE 11 Maths is the benchmark for any student that will reflect in the future records of achievement. CBSE strictly follows the NCERT books for board exam preparation. CBSE Class 11 Maths Solutions of NCERT is the best tool for students in the preparation of final and competitive entrance exams.
How to score good marks in Class 11 Maths exams?
The NCERT Solutions for Class 11 Maths are revised and updated for new session following the new NCERT textbooks published for 2024-25 exams. Preparing for Class 11 mathematics using NCERT solutions is an excellent strategy as NCERT textbooks are a primary resource for the CBSE curriculum. Here’s a step-by-step guide on how to prepare for Class 11 math with NCERT solutions.
- Step 1: Acquire the Necessary Materials from online learning platforms like Tiwari Academy.
- Step 2: Read the NCERT Textbook and Use NCERT Solutions to verify the answers.
- Step 3: Review and Understand, Practice Regularly and Take Notes.
- Step 4: Focus on Self-Assessment, Stay Organised and Healthy.
- Step 5: Be updated and Manage Exam Stress by solving Previous Year Papers.
Step 1: Acquire the Necessary Materials from online learning platforms like Tiwari Academy.
Obtain the Class 11 NCERT mathematics textbook. Access NCERT Solutions for Class 11 math, which are available online on various educational websites or can be found in bookstores. Read and understand the Class 11 CBSE Maths syllabus for 2024-25. It’s essential to know what topics and concepts you need to cover. Develop a well-structured study timetable that allocates specific time slots for math. Balance your study time according to the difficulty level and your personal preferences.Step 2: Read the NCERT Textbook and Use NCERT Solutions to verify the answers.
Begin by thoroughly reading the NCERT mathematics textbook for Class 11. Pay attention to explanations, examples, and illustrations. After studying a chapter or section in the textbook, use the corresponding NCERT Solutions to reinforce your understanding. Solve the exercises and problems in the textbook before referring to the solutions. This will help you gauge your initial understanding. After attempting the exercises, compare your answers with the solutions provided in the NCERT Solutions book. Identify and analyze any mistakes you’ve made.Step 3: Review and Understand, Practice Regularly and Take Notes.
If you made errors, review the solutions and try to understand where you went wrong. Analyze the correct methods used in the solutions. Consistent practice is essential for mathematics. Solve a variety of problems from each chapter, including additional practice problems beyond the textbook. While studying, take concise notes of important formulas, concepts, and key points. These notes will serve as quick references during revision. If you have doubts or find certain topics challenging, don’t hesitate to seek help from your math teacher, classmates, or online resources.Step 4: Focus on Self-Assessment, Stay Organised and Healthy.
Step 5: Be updated and Manage Exam Stress by solving Previous Year Papers.
As the exams approach, practice stress management techniques such as deep breathing, meditation, and time management to stay calm and focused. Try to solve previous years’ CBSE board exam papers. This will give you an idea of the exam pattern and help you manage your time effectively during the actual exam. Keep an eye on any updates or changes in the exam pattern or question format from CBSE. With dedication and the right strategy, you can excel in your Class 11 math exams.How can Tiwari Academy’s NCERT Solutions for Class 11 Maths help in achieving high test results?
The Tiwari Academy’s subject expert teachers have organized the NCERT Solutions around the CBSE board’s curriculum. They provide CBSE NCERT Solutions for Class 11 Maths with a wide range of solved problems, which can be very helpful in achieving high test results. The questions are solved by expert math teachers, who have a lot of experience in teaching the subject. In addition, the NCERT solutions are available for download on the Tiwari Academy’s website.
How many Chapters are there in Maths Class 11 Exam?
According to new rationalised textbooks published for 2024-25 exams, there are total of 14 chapters in Maths class 11 for first and second term examination.
Is Maths difficult in Class 11?
Some students find the Class 11 Maths is hard, as they are introduced new topics in class 11. And also the syllabus of class 11 Maths is extremely vast as compared to previous class 10. And students get worried about the vast new syllabus. But NCERT Solutions for Class 11 Maths for all chapters help you to clear all concepts and you can score good marks in your exam.
Is NCERT enough for class 11 Maths?
NCERT is the best resources for preparing CBSE Board Examinations for the class 11. NCERT not only help you to score good marks in exam but also prepare for all the academic and undergraduate Competitive Entrance Examinations.
How NCERT Solutions will Help You Get Better Marks in Class 11 Maths?
NCERT Solutions for Class 11 Maths will make all the chapter sums easier for you to understand the concept so that you can learn how to give excellent answers in the CBSE Class 11 exams. NCERT Solutions will help in clearing all your doubts about the subject Maths.
