NCERT Solutions for Class 5 Maths Mela Chapter 11 Grandmother’s Quilt

Page 142

Preetha and Adrit’s grandmother made a quilt cover using old clothes. Now she wants to decorate it with lace. Tick the lace option that would cover the entire border of the quilt. She decides to use two different coloured laces. How much lace of each kind will be needed to cover the entire border?

Answer:
Counting the small equal units (squares) along the border of the quilt in the picture:
Top side = 15 units
Bottom side = 15 units
Left side = 10 units
Right side = 10 units
Perimeter means total length of the boundary.
Perimeter = 15 + 15 + 10 + 10 = 50 units
So, the perimeter of the quilt is 50 units
Given lace options:
Red lace = 40 units
Green lace = 50 units
Blue lace = 25 units
She uses two different colours, she can divide the border into two equal parts:
50 ÷ 2 = 25 units each
Available lace of 25 units: Blue lace = 25 units
So she can use:
Blue lace – 25 units
Green lace – 25 units(half of the green roll)

Page 142

Let Us Do

1. Find the perimeter of the following shapes. All sides of the following shapes are equal.

Answer:
Perimeter means the total length around the shape.
Perimeter = Number of sides × Length of one side
The shape is pentagon and has 5 sides. Each side is 4 cm long.
Perimeter = 5 × 4 = 20 cm
The shape is joined triangles there are 6 equal sides in total. Each side is 5 cm long.
Perimeter = 6 × 5 = 30 cm

2. Draw two rectangles each having the following perimeters.
(a) 26 cm
(b) 18 cm
Answer:

Page 143

Preetha and Adrit’s grandmother is making a rug with square patches. The picture below shows the rug. How many patches have they used to make this?

Answer:
A row is a line of patches that goes across the rug (from left to right).
There are 6 rows of patches in the rug.
A column is a line of patches that goes up and down the rug (from top to bottom).
There are 15 columns of patches.
Total Patches = Number of Rows × Number of Columns
Total Patches = 6 × 15 = 90
Preetha and Adrit’s grandmother has used 90 patches to make the rug.

Preetha and Adrit are trying to cover their table with different shapes. Preetha covered it with triangles and circles. Adrit covered with squares and rectangles.

They found that __________, __________ and __________ shapes cover the top of the table without gaps and overlaps. __________ shape leaves gaps. __________ triangles cover Table 1 __________ squares cover Table 3 __________ rectangles cover Table 4.
Answer:
They found that “triangles”, “squares” and “rectangles” shapes cover the top of the table without gaps and overlaps. “Circle” shape leaves gaps. “20” triangles cover Table 1. “8” squares cover Table 3. “6” rectangles cover Table 4.

To find the area of a region, we usually fill it with shapes that tile (no gaps and overlaps), like squares, rectangles and triangles.
Do circles tile? Can we use them to cover a region?
The area of Table 1 is __________ triangle units.
The area of Table 3 is __________ square units.
The area of Table 4 is __________ rectangle units.
Answer:
Circles do not tile because their curvy edges leave empty gaps between them, and a true tile must cover the floor perfectly without any holes.
As we can see in Table 2, when we use circles, there are gaps left between them and at the edges. Tiling requires covering a region with no gaps and no overlaps.
The area of Table 1 is “20” triangle units.
The area of Table 3 is “8” square units.
The area of Table 4 is “12” rectangle units.

Page 144

Let Us Do

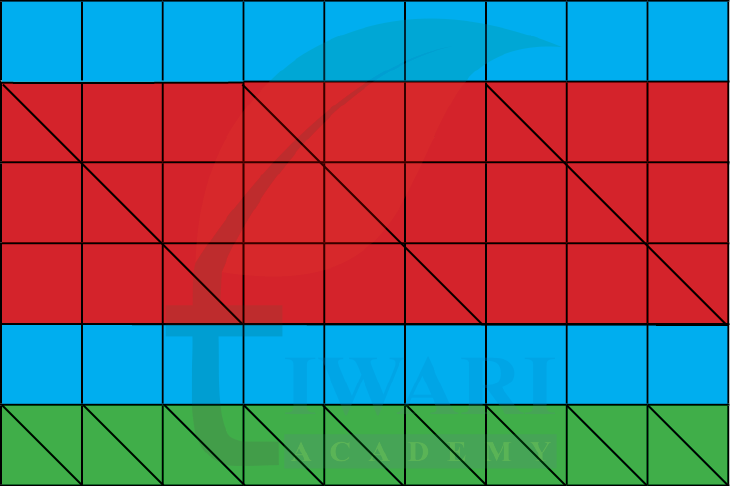
Preetha is playing with tiles. She covers her desk with different shapes as shown below. Look at the different tiles on her desk and answer how many of the following shapes will cover the desk.
(a) Green triangles __________
(b) Red triangles __________
(c) Blue squares __________

Answer:
(a) Green triangles = 18
(b) Red triangles = 6
(c) Blue squares = 18

Page 144

Comparing Shapes

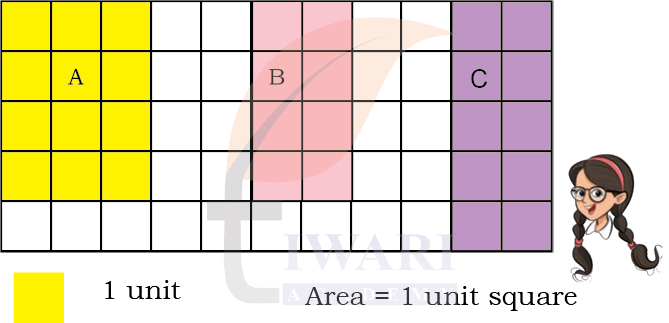
Which of the above rectangles has the largest area? Trace these shapes on to a paper and cut them to find out the one that has the largest area. Do you see that the area of rectangle A is larger than that of B? What about B and C?
Answer:
Rectangle A (Yellow):
It covers 4 rows and 3 columns
That’s 4 × 3 = 12 unit squares
Rectangle B (Pink):
It covers 4 rows and 2 columns
That’s 4 × 2 = 8 unit squares
Rectangle C (Purple):
It covers 5 rows and 2 columns
That’s 5 × 2 = 10 unit squares
So, rectangle A has the largest area and rectangle C is larger than B.

Page 145

Let Us Do

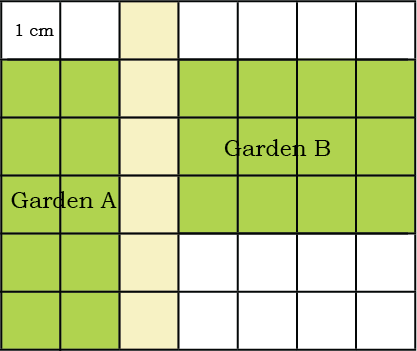
1. Compare the areas of the two gardens given below on the square grid. Share your observations.
Area of Garden A = _____ cm square
Area of Garden B = _____ cm square

Answer:
Garden A is 2 columns wide 5 rows tall
Area of Garden A = 2 × 5 = 10 cm square​
Garden B is 4 columns wide 3 rows tall
Area of Garden B = 4 × 3 = 12 cm square

2. Trace your palm on the square grid given below and find the approximate area of your palm. Compare the area of your palm with your friend’s palm. Who has a bigger palm?

Answer:
Area of my palm: 27 square units (approx.)
Area of my friend’s palm: 26 square units (approx.)
My palm is slightly larger than my friend.

3. Collect leaves of different kinds. Put them on a square grid and find their area.
(a) Name the leaf with the largest area.
(b) Name the leaf with the smallest area.
Answer:
Mango leaf: Long, narrow leaf at the top, Area = 78 square units
Peepal leaf: Heart-shaped leaf, Area = 44 square units
Neem leaf (single leaflet): Small, serrated leaf, Area = 15 square units
Tulsi (Holy Basil) leaves: Cluster of small oval leaves, Area = 9 square units
Maple leaf: Broad leaf with pointed lobes, Area = 73 square units
Curry leaf: Thin, long blade, Area = 47 square units.

4. The following mats are made of square patches of equal size. How many square patches will be required to cover each mat? Would both mats require an equal or different number of patches? Trace and cut out a small square of the size give below and find the area.

Answer:
(a) Counting the number of orange patches fit in length and width:
Length: 5 patches
Width: 2 patches
So total patches = 5 × 2 = 10
Area of mat = 10 square units
Perimeter of mat (a) = 2 × (length + width)
= 2 × (5 + 2)
= 14 units

(b) Count how many orange patches fit in:
Length: 4 patches
Width: 3 patches
So total patches = 4 × 3 = 12 patches
Area of mat = 12 square units
Perimeter of mat (b) = 2 × (4 + 3) = 14 units

Trisha makes these two rectangles. She says, “I increased the area of my rectangle, and the perimeter increased.” Do you think this is always true?

Answer:
Left Rectangle (Small One)
2 blocks wide
3 blocks tall
So, total blocks (Area) = 2 × 3 = 6 square units
Perimeter = 2 × (length + width)
= 2 × (3 + 2)
= 2 × 5
= 10 units
Right Rectangle (Bigger One)
3 blocks wide
4 blocks tall
So, total blocks (Area) = 3 × 4 = 12 square units
Perimeter = 2 × (length + width)
= 2 × (4 + 3)
= 2 × 7
= 14 units
Yes, When Trisha increased the area, the perimeter also increased.
But it is not always true.
Example:
Rectangle A:
Length = 6 and Width = 1
Area = L x W = 6 × 1 = 6 square units
Perimeter = 2 × (length + width) = 2 × (6 + 1) = 14 units
Rectangle B:
Length = 4 and Width = 3
Area = L x W = 4 × 3 = 12 square units
Perimeter = 2 × (length + width) = 2 × (4 + 3) = 14 units
Since we increased the area, but the perimeter didn’t increase.

Page 147

Let Us Explore

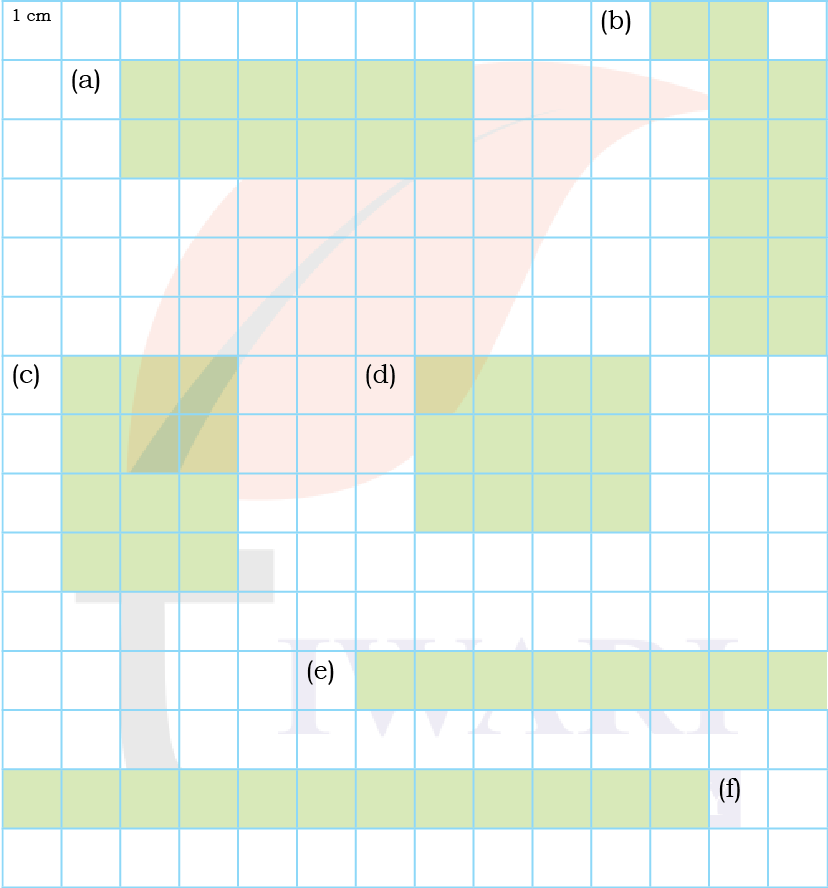
1. Tick the shapes with the same area. Find the perimeters of these shapes. What do you notice? Discuss.

Answer:
(a) Length = 6 units
Width = 2 units
Area = L x W = 6 x 2 = 12 square units
Perimeter = 2 × (length + width) = 2 (6 + 2) = 16 units

(b) Length = 2 units
Width = 6 units
Area = L x W = 2 x 6 = 12 square units
Perimeter = 2 × (length + width) = 2 (2 + 6) = 16 units

(c) Length = 3 units
Width = 4 units
Area = L x W = 3 x 4 = 12 square units
Perimeter = 2 × (length + width) = 2(3 + 4) = 14 units

(d) Length = 4 units
Width = 3 units
Area = L x W = 4 x 3 = 12 square units
Perimeter = 2 × (length + width) = 2(4 + 3) = 14 units

(e) Length = 8 units
Width = 1 unit
Area = L x W = 8 x 1 = 8 square units
Perimeter = 2 × (length + width) = 2(8 + 1) = 18 units

(f) Length = 12 units
Width = 1 unit
Area = L x W = 12 x 1 = 12 square units
Perimeter = 2 × (length + width) = 2(12 + 1) = 26 units
In the given figures, a, b, c and d have same area but the perimeter is not same.

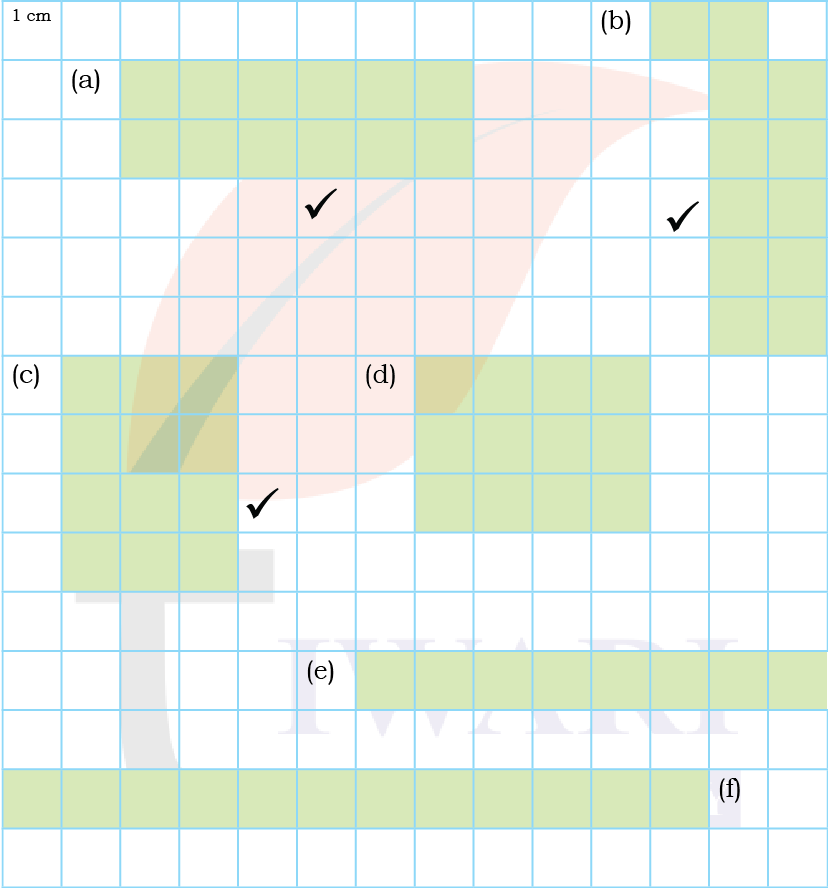
2. Tick the shapes with the same perimeter. Find the areas of these shapes. What do you notice? Discuss.

Answer:
(a) Area: 7 square units
Perimeter: 12 units

(b) Area: 7 square units
Perimeter: 12 units

(c) Area: 7 square units
Perimeter: 16 units

(d) Area: 7 square units
Perimeter: 16 units

(e) Area: 7 square units
Perimeter: 16 units
The perimeter of a as well as b are 12 units whereas the perimeter of c, d and are 16 units, even though they are arranged in different forms.
The area of all shapes is also the same (7 square units).
This shows that shapes with the same area and perimeter can have different arrangements but cover the same space and have the same boundary length.

Page 149

Let Us Do

1. Draw different shapes having the same area as the given shape. Write the perimeter of each shape. What do you notice? Discuss.

Answer:
Perimeter of (a): 22 units
Perimeter of (b): 26 units
Perimeter of (c): 20 units
Perimeter of (d): 38 units
Perimeter of (e): 38 units
Perimeter of (f): 38 units
In spite of being same in area they have different perimeters. This is because of their orientation.

2. Is the area of shape (a) less than the area of shape (b) given below? Discuss.
What are the other ways of finding area?

Answer:
No, the area of shape (a) is not less than the area of shape (b).
In fact, both shapes have the same area.
Shape (a) covers 9 unit squares.
Shape (b) also covers the same 9 unit squares.
So, although the shapes look different, their areas are equal.
Area of shape (a) = Area of shape (b)

Preetha and Adrit’s grandmother is making another square patchwork.
She arranges the patches as shown below. Can you guess how many patches she will need? How did you find it?

Answer:
She will need 15 patches.
The way of finding area:
There are 5 rows of 3 patches each. That is 6 × 4 = 24 patches.

Page 151

Let Us Do

1. Find the area of your classroom floor in square meters. Take the help of your teacher to measure the length and breadth of the floor. What is the perimeter of the classroom floor?
Answer:
With the help of my teacher, I measured the classroom floor.
Length of the classroom = 8 meters
Breadth of the classroom = 6 meters
Area = Length × Breadth
Area = 8 × 6 = 48 square meters
So, the area of my classroom floor is 48 square meters.
Perimeter = 2 × (Length + Breadth)
Perimeter = 2 × (8 + 6) = 2 × 14 = 28 meters
So, the perimeter of my classroom floor is 28 meters.

2. Find the area and perimeter of the following shapes.

Answer:
(a) Length = 6 cm
Width = 6 cm
Area = Length × Width = 6 cm × 6 cm = 36 cm²
Perimeter = 2 × (Length + Width)
= 2 × (6 cm + 6 cm) = 2 × 12 cm = 24 cm.

(b) Length = 7 cm
Width = 4 cm
Area = Length × Width = 7 cm × 4 cm = 28 cm²
Perimeter = 2 × (Length + Width)
= 2 × (7 cm + 4 cm) = 2 × 11 cm = 22 cm

(c) Length = 12 cm
Width = 4 cm
Area = Length × Width = 12 cm × 4 cm = 48 cm²
Perimeter = 2 × (Length + Width)
= 2 × (12 cm + 4 cm) = 2 × 16 cm = 32 cm

(d) Length = 3 cm
Width = 3 cm
Area = Length × Width = 3 cm × 3 cm = 9 cm²
Perimeter = 2 × (Length + Width)
= 2 × (3 cm + 3 cm) = 2 × 6 cm = 12 cm

(e) Length = 6 cm
Width = 5 cm
Area = Length × Width = 6 cm × 5 cm = 30 cm²
Perimeter = 2 × (Length + Width)
= 2 × (6 cm + 5 cm) = 2 × 11 cm = 22 cm

3. Find the area and perimeter of the following objects. Use a scale or measuring tape to find the length and the breadth of each of the objects.

Answer:
Cover of the Notebook:
Length = 0.30 m, Breadth = 0.20 m
Area = 0.30 × 0.20 = 0.06 sq m
Perimeter = 2 × (0.30 + 0.20) = 1.00 m

Newspaper:
Length = 0.60 m, Breadth = 0.40 m
Area = 0.60 × 0.40 = 0.24 sq m
Perimeter = 2 × (0.60 + 0.40) = 2.00 m

Blackboard:
Length = 2.00 m, Breadth = 1.20 m
Area = 2.00 × 1.20 = 2.40 sq m
Perimeter = 2 × (2.00 + 1.20) = 6.40 m

Ludo Board:
Length = 0.45 m, Breadth = 0.45 m
Area = 0.45 × 0.45 = 0.2025 sq m
Perimeter = 2 × (0.45 + 0.45) = 1.80 m

My Study Table:
Length = 1.20 m, Breadth = 0.60 m
Area = 1.20 × 0.60 = 0.72 sq m
Perimeter = 2 × (1.20 + 0.60) = 3.60 m

Bedsheet:
Length = 2.00 m, Breadth = 1.50 m
Area = 2.00 × 1.50 = 3.00 sq m
Perimeter = 2 × (2.00 + 1.50) = 7.00 m

4. Find the area of a rectangular field whose length is 42 m and breadth is 34 m.
Answer:
Length = 42 m
Breadth = 34 m
Area = Length × Breadth
Area = 42 m × 34 m = 1428 square meters.
So, the area of the rectangular field is 1,428 square meters.

5. The area of a rectangular garden is 64 square m and its length is 16 m. What is its breadth?
Answer:
Area = 64 square meters
Length = 16 meters (m)
Area = Length × Breadth
64 square meters = 16 m × Breadth
Breadth = 64 ÷ 16
Breadth = 4 m

6. Find the area of the following figure with the dimensions as marked in the figure.

Answer:
Total Length = 32 cm
The total width is divided into two sections on the left side:
The top section is 6 cm.
The bottom section is 12 cm.
Total Width = 6 cm + 12 cm = 18 cm
Area = Length × Width
Area = 32 cm × 18 cm
Area = 576 square cm