NCERT Solutions for Class 10 Maths updated for session 2024-25 in Hindi and English Medium. Get the revised Class 10 Maths solutions based on the new syllabus and reduced course for the 2024-25 session. These solutions are perfectly aligned with CBSE guidelines and available in both Hindi and English, ensuring students can easily access and understand the concepts.
Syllabus and NCERT Solutions Class 10 Maths
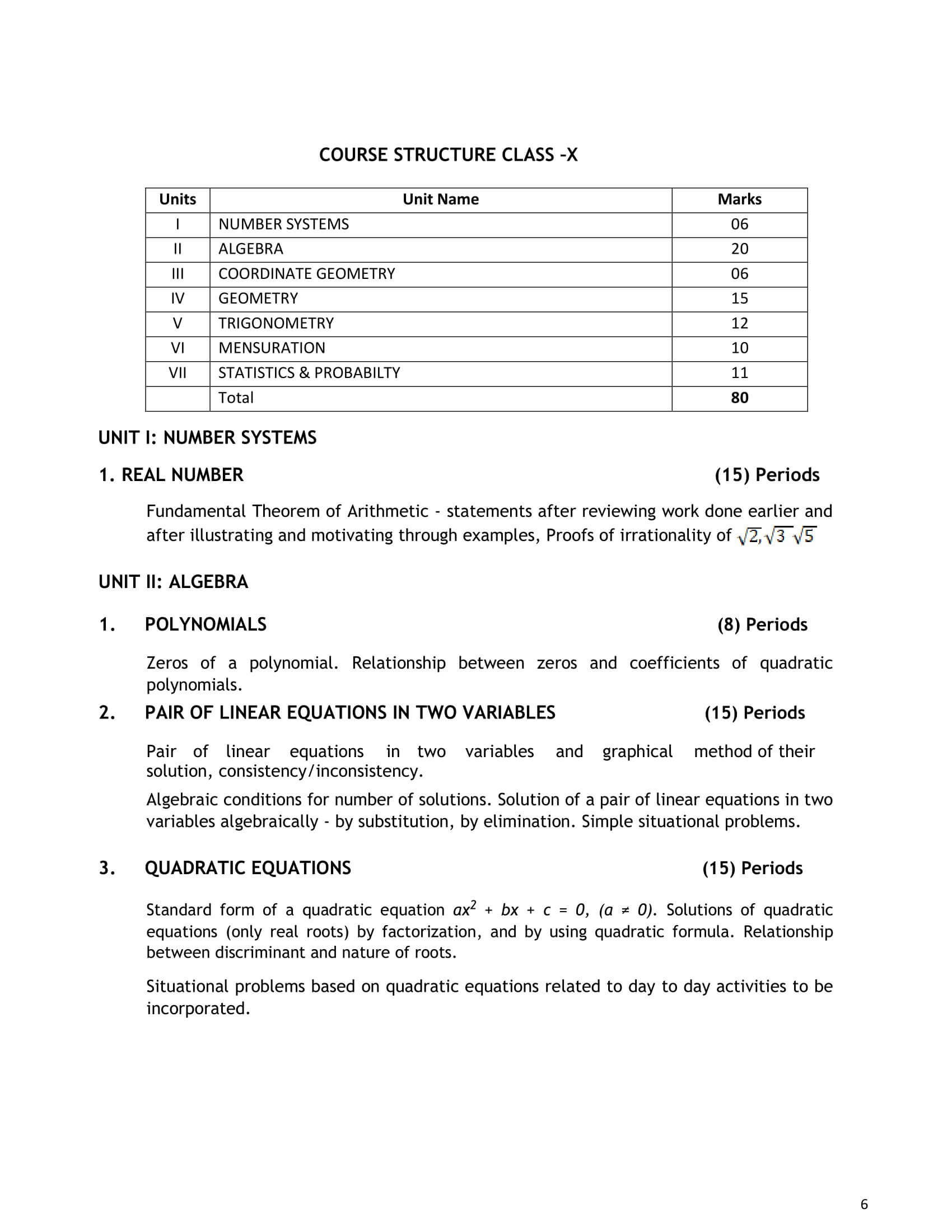
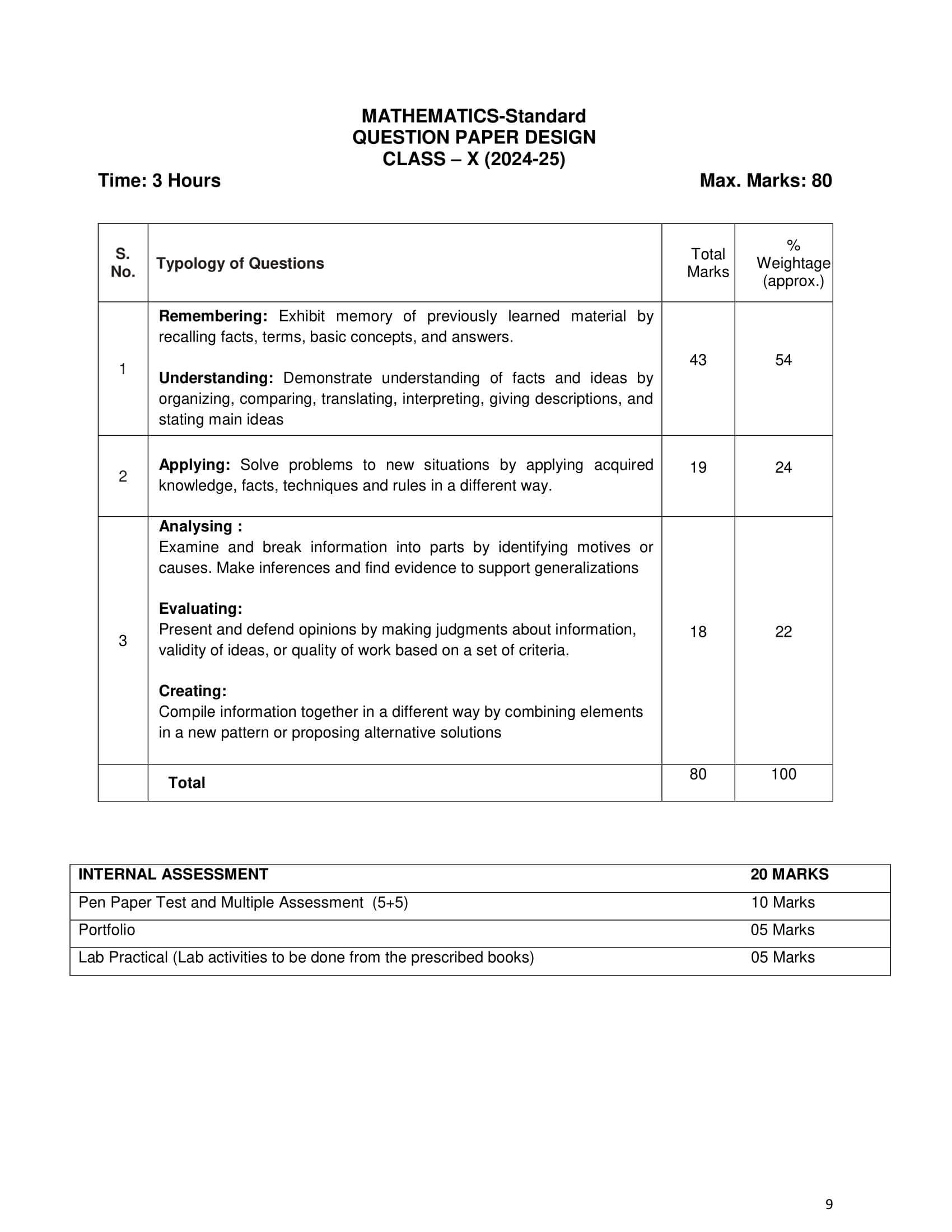
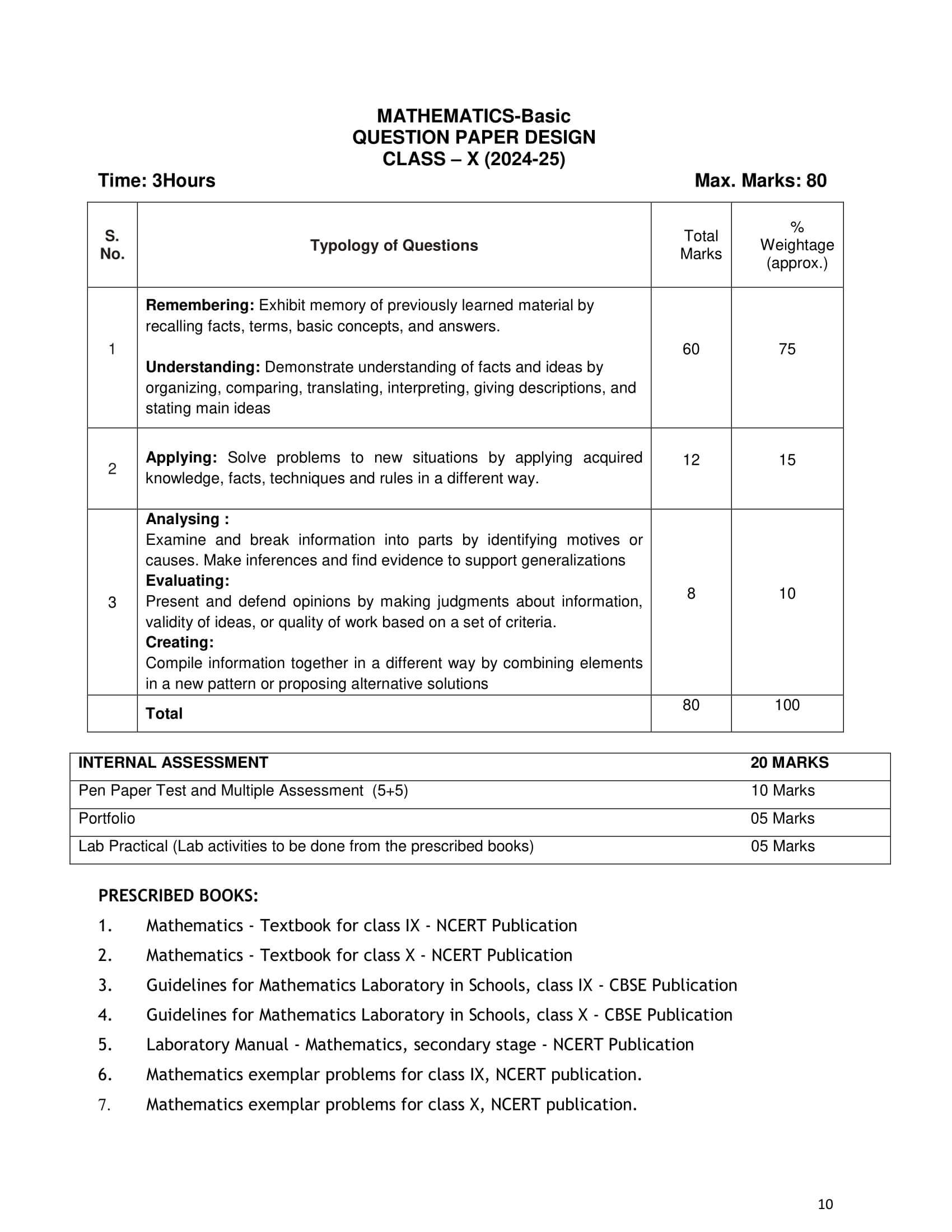
CBSE Syllabus Class 10 Maths for 2024-25
Chapter 1. Real Numbers
Chapter 2. Polynomials
Chapter 3. Pair of Linear Equations
Chapter 4. Quadratic Equations
Chapter 5. Arithmetic Progression
Chapter 6. Triangles
Chapter 7. Coordinate Geometry
Chapter 8. Introduction to Trigonometry
Chapter 9. Applications of Trigonometry
Chapter 10. Circles
Chapter 11. Area Related to Circles
Chapter 12. Surface Areas and Volumes
Chapter 13. Statistics
Chapter 14. Probability
Weightage of Chapters: Class 10 Maths for Board Exam 2024-25
| Chapters | Weightage (Marks) |
|---|---|
| 1. Real Numbers | 06 |
| 2. Polynomials, 3. Pair of Linear Equations, 4. Quadratic Equations, 5. Arithmetic Progression | 20 |
| 7. Coordinate Geometry | 06 |
| 6. Triangles, 10. Circles | 15 |
| 8. Introduction to Trigonometry, 9. Applications of Trigonometry | 12 |
| 11. Area Related to Circles, 12. Surface Areas and Volumes | 10 |
| 13. Statistics, 14. Probability | 11 |
| Pen Paper Test and Multiple Assessment | 10 |
| Portfolio | 05 |
| Lab Practical (Lab activities to be done from the prescribed books) | 05 |
| Total | 100 |
Check here the 10th NCERT Solutions with complete Curriculum of Class 10 Maths for 2024-25 Board Exams. Class 10 Maths Solution Guides Available in Hindi and English Medium. At Tiwari Academy, our Class 10 Maths solutions are designed to be both accurate and easy to understand, ensuring students in both Hindi and English medium can confidently grasp mathematical concepts. Trust our expertly crafted solutions for simplified learning and effective exam preparation. Rate and Review with your feedback.
Class 10 Solutions Apps Download
Class 10 Maths NCERT Solutions at Tiwari Academy: Trusted by Students and Teachers. Our Class 10 Maths NCERT solutions follow the CBSE-prescribed curriculum, ensuring accuracy and reliability. At Tiwari Academy, we provide detailed, step-by-step explanations of mathematical concepts, formulas and problem-solving techniques, helping students master the subject with ease. Ideal for exam preparation and classroom learning.

Here are the tips to score good marks in 10th Maths, student need more practice preparing for a class 10 Maths exam.
1. Regular practice helps to reinforce or cement the mathematical concepts already learnt in class 10. Remember the saying that PRACTICE MAKES A MAN PERFECT. Towards this end, Tiwari Academy provides simple solutions which are user friendly.
2. By Making use of these solutions, the understanding of 10th Mathematics as a practical tool in solving day to day problems become possible.
3. Further, scoring marks in class 10 mathematics becomes a child’s play.
Students of grade 10 mathematics, finds here the revised and modified Class 10 Maths NCERT solutions based on new curriculum.
Class 10 Mathematics Revised Syllabus for 2024-25
| Class: 10 | Mathematics |
| Number of Chapters: | 14 (Fourteen) |
| Contents: | NCERT Exercises, Extra Questions, Test Papers |
| Content Type: | Text, Videos, Images and PDF Format |
| Academic Year: | Session 2024-25 |
| Medium: | English and Hindi Medium |
Class 10 Solution Apps
Solutions of all exercises from Chapters 1 to 14 are available in PDF at Tiwari Academy. The NCERT textbook solutions for class 10 Maths are made easy to understand. These concepts help to score good marks in school test and also in the board exams class 10 mathematics.
Perfection in Class 10 Mathematics needs constant practice. Ideally, few examples and few unsolved questions based on those examples need to be practised. A variety of questions should be solved because there has been change in the examination pattern.
NCERT Solutions for Class 10 Maths Chapter 1 – Real Numbers
In Class 10 Maths Chapter 1, Real Numbers, student learn about a detailed knowledge in real numbers and irrational numbers. Learn about Euclid’s Division Lemma and the Fundamental Theorem of Arithmetic in-depth. Download all the exercises of Class 10 Maths Chapter 1 in PDF format right here. These resources provide detailed explanations and step-by-step solutions to help students master the concepts with ease. Perfect for exam preparation and daily practice!
Class 10 Maths Chapter 1 in English for CBSE Board
Class 10 Maths Exercise 1.1 in English
Class 10 Maths Exercise 1.2 in English
Class 10 Maths Chapter 1 in English for State Board
Class 10 Maths Exercise 1.1 in English
Class 10 Maths Exercise 1.2 in English
Class 10 Maths Exercise 1.3 in English
Class 10 Maths Exercise 1.4 in English
Tiwari Academy’s NCERT solutions are available in both English and Hindi which makes it accessible to students from both language backgrounds.
Class 10 Maths Chapter 1 in Hindi Medium
Class 10 Maths Exercise 1.1 in Hindi
Class 10 Maths Exercise 1.2 in Hindi
Topics to be covered in Class 10 Maths Chapter 1 Real Numbers
Fundamental Theorem of Arithmetic – statements after reviewing work done earlier and after illustrating and motivating through examples, Proofs of irrationality of √2, √3 and √5.
NCERT Solutions for Class 10 Maths Chapter 2 – Polynomials
Student get Class 10 Maths NCERT Solutions Chapter 2 Polynomials with free of cost.
Class 10 Maths Chapter 2 in English for CBSE Board
Class 10 Maths Exercise 2.1 in English
Class 10 Maths Exercise 2.2 in English
Class 10 Maths Chapter 2 in English for State Board
Class 10 Maths Exercise 2.1 in English
Class 10 Maths Exercise 2.2 in English
Class 10 Maths Exercise 2.3 in English
Class 10 Maths Exercise 2.4 in English
Tiwari Academy offers free NCERT solutions, making it a great resource for students looking to excel in their Class 10 Maths exams. These solutions are easy to understand and help build a strong foundation for future success. Ideal for exam preparation and mastering essential concepts.
Class 10 Maths Chapter 2 in Hindi Medium
Class 10 Maths Exercise 2.1 in Hindi
Class 10 Maths Exercise 2.2 in Hindi
Class 10 Maths Chapter 2 Polynomials Topics for Exams
Zeros of a polynomial. Relationship between zeros and coefficients of quadratic polynomials.
NCERT Solutions for Class 10 Maths Chapter 3 – Pair of Linear Equations in Two Variables
Class 10 Maths chapter 3 explains the concept of Pair of Linear Equations in Two Variables.
Class 10 Maths Chapter 3 in English for CBSE Board
Class 10 Maths Exercise 3.1 in English
Class 10 Maths Exercise 3.2 in English
Class 10 Maths Exercise 3.3 in English
Class 10 Maths Chapter 3 in English for State Board
Class 10 Maths Exercise 3.1 in English
Class 10 Maths Exercise 3.2 in English
Class 10 Maths Exercise 3.3 in English
Class 10 Maths Exercise 3.4 in English
Class 10 Maths Exercise 3.5 in English
Class 10 Maths Exercise 3.6 in English
Class 10 Maths Exercise 3.7 in English
Class 10 Maths Chapter 3 in Hindi Medium
Class 10 Maths Exercise 3.1 in Hindi
Class 10 Maths Exercise 3.2 in Hindi
Class 10 Maths Exercise 3.3 in Hindi
Main Topics of Class 10 Maths Chapter 3 Pair of Linear Equations in two Variables
Pair of linear equations in two variables and graphical method of their solution, consistency/inconsistency. Algebraic conditions for number of solutions. Solution of a pair of linear equations in two variables algebraically – by substitution, by elimination. Simple situational problems.
NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations
Class 10 Maths chapter 4 provides help to know about the standard form of writing a quadratic equation.
Class 10 Maths Chapter 4 in English for CBSE Board
Class 10 Maths Exercise 4.1 in English
Class 10 Maths Exercise 4.2 in English
Class 10 Maths Exercise 4.3 in English
Class 10 Maths Chapter 4 in English for State Board
Class 10 Maths Exercise 4.1 in English
Class 10 Maths Exercise 4.2 in English
Class 10 Maths Exercise 4.3 in English
Class 10 Maths Exercise 4.4 in English
Class 10 Maths Chapter 4 in Hindi Medium
Class 10 Maths Exercise 4.1 in Hindi
Class 10 Maths Exercise 4.2 in Hindi
Class 10 Maths Exercise 4.3 in Hindi
Class 10 Maths Chapter 4 Quadratic Equations Topics
Standard form of a quadratic equation ax² + bx + c = 0, (a ≠ 0). Solutions of quadratic equations (only real roots) by factorization, and by using quadratic formula. Relationship between discriminant and nature of roots. Situational problems based on quadratic equations related to day to day activities to be incorporated.
NCERT Solutions for Class 10 Maths Chapter 5 – Arithmetic Progressions
Class 10 Maths chapter 5 introduces new topic that is Arithmetic Progression which is also known as A.P. Its importance carry on in next classes also.
Class 10 Maths Chapter 5 in English CBSE and State Board
Class 10 Maths Exercise 5.1 in English
Class 10 Maths Exercise 5.2 in English
Class 10 Maths Exercise 5.3 in English
Class 10 Maths Exercise 5.4 in English
Class 10 Maths Chapter 5 in Hindi Medium
Class 10 Maths Exercise 5.1 in Hindi
Class 10 Maths Exercise 5.2 in Hindi
Class 10 Maths Exercise 5.3 in Hindi
Class 10 Maths Exercise 5.4 in Hindi
Class 10 Maths Chapter 5 Arithmetic Progressions Topics for Board Exams
Motivation for studying Arithmetic Progression Derivation of the nth term and sum of the first n terms of A.P. and their application in solving daily life problems.
NCERT Solutions for Class 10 Maths Chapter 6 – Triangles
In Class 10th Maths chapter 6, learn about study those figures which have the same shapes but not necessarily the same size.
Class 10 Maths Chapter 6 in English for CBSE Board
Class 10 Maths Exercise 6.1 in English
Class 10 Maths Exercise 6.2 in English
Class 10 Maths Exercise 6.3 in English
Class 10 Maths Chapter 6 in English for State Board
Class 10 Maths Exercise 6.1 in English
Class 10 Maths Exercise 6.2 in English
Class 10 Maths Exercise 6.3 in English
Class 10 Maths Exercise 6.4 in English
Class 10 Maths Exercise 6.5 in English
Class 10 Maths Exercise 6.6 in English
Class 10 Maths Chapter 6 in Hindi Medium
Class 10 Maths Exercise 6.1 in Hindi
Class 10 Maths Exercise 6.2 in Hindi
Class 10 Maths Exercise 6.3 in Hindi
Class 10 Maths Chapter 6 Triangles Topics to be Covered
Definitions, examples, counter examples of similar triangles.
Only Theorem 1, (If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio) can be asked for proof in class 10 Maths board exams 2024-25. Rest will be used for concepts to apply in questions solving.
Theorem 2: If a line divides two sides of a triangle in the same ratio, the line is parallel to the third side. (Motivate)
Theorem 3: If in two triangles, the corresponding angles are equal, their corresponding sides are proportional and the triangles are similar. (Motivate)
Theorem 4: If the corresponding sides of two triangles are proportional, their corresponding angles are equal and the two triangles are similar. (Motivate)
Theorem 5: If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional, the two triangles are similar. (Motivate)
NCERT Solutions for Class 10 Maths Chapter 7– Coordinate Geometry
Class X Maths chapter 7 explains that how to find the distance between two points if the coordinates are given.
Class 10 Maths Chapter 7 in English for CBSE Board
Class 10 Maths Exercise 7.1 in English
Class 10 Maths Exercise 7.2 in English
Class 10 Maths Chapter 7 in English for CBSE Board
Class 10 Maths Exercise 7.1 in English
Class 10 Maths Exercise 7.2 in English
Class 10 Maths Exercise 7.3 in English
Class 10 Maths Exercise 7.4 in English
To prepare for Class 10 Maths using Tiwari Academy online educational platform, visit the website and navigate to the Class 10 Maths NCERT solutions section and the relevant resource area.
Class 10 Maths Chapter 7 in Hindi Medium
Class 10 Maths Exercise 7.1 in Hindi
Class 10 Maths Exercise 7.2 in Hindi
Class 10 Maths Solutions Chapter 7 Coordinate Geometry Main Points to Study
Concepts of coordinate geometry, graphs of linear equations. Distance formula. Section formula (internal division).
NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry
Get here 10th Maths chapter 8 provided by the Maths expert of Tiwari Academy.
Class 10 Maths Chapter 8 in English for CBSE Board
Class 10 Maths Exercise 8.1 in English
Class 10 Maths Exercise 8.2 in English
Class 10 Maths Exercise 8.3 in English
Class 10 Maths Chapter 8 in English for State Board
Class 10 Maths Exercise 8.1 in English
Class 10 Maths Exercise 8.2 in English
Class 10 Maths Exercise 8.3 in English
Class 10 Maths Exercise 8.4 in English
Class 10 Maths Chapter 8 in Hindi Medium
Class 10 Maths Exercise 8.1 in Hindi
Class 10 Maths Exercise 8.2 in Hindi
Class 10 Maths Exercise 8.3 in Hindi
Class 10 Maths Chapter 8 Introduction to Trigonometry Topics for Session 2024-25
Trigonometric ratios of an acute angle of a right-angled triangle. Proof of their existence (well defined); motivate the ratios whichever are defined at 0o and 90o. Values of the trigonometric ratios of 30°, 45°, and 60°. Relationships between the ratios. Proof and applications of the identity sin²A + cos²A = 1. Only simple identities to be given.
NCERT Solutions for Class 10 Maths Chapter 9 – Some Applications of Trigonometry
Learn here the different ways to solve Class 10 Maths chapter 9 questions using diagrams. All sums in Tiwari Academy’s NCERT solutions for Class 10 Maths are well explained and solved using simple methods, helping students clear their doubts easily. In Chapter 9, Some Applications of Trigonometry, the focus is on one main topic: height and distance. This makes it easier for students to grasp the concepts and apply them confidently in exams.
Class 10 Maths Chapter 9 in English for CBSE and State Board
Class 10 Maths Exercise 9.1 in English
Class 10 Maths Chapter 9 in Hindi Medium
Class 10 Maths Exercise 9.1 in Hindi
Class 10 Maths Chapter 9 Applications of Trigonometry Focus Points
Angle of elevation, Angle of Depression. Simple problems on heights and distances. Problems should not involve more than two right triangles. Angles of elevation / depression should be only 30°, 45°, and 60°.
NCERT Solutions for Class 10 Maths Chapter 10 Circles
Find here the best Class 10 Maths chapter 10 solutions explained through figures and diagrams. Chapter 10 of Class 10 Maths covers two key topics: the tangent at any point of a circle and the lengths of tangents drawn from an external point to the circle. These concepts are explained clearly, making it easier for students to understand and apply them in problem-solving. Perfect for exam preparation and concept clarity.
Class 10 Maths Chapter 10 in English for CBSE and State Board
Class 10 Maths Exercise 10.1 in English
Class 10 Maths Exercise 10.2 in English
Class 10 Maths Textbook Solution Chapter 10 in Hindi Medium
Class 10 Maths Exercise 10.1 in Hindi
Class 10 Maths Exercise 10.2 in Hindi
The Main points of Class 10 Maths Chapter 10 Circles
Tangent to a circle at, point of contact.
1. (Prove) The tangent at any point of a circle is perpendicular to the radius through the point of contact.
2. (Prove) The lengths of tangents drawn from an external point to a circle are equal.
NCERT Solutions for Class 10 Maths Chapter 11 Areas Related to Circles
Download Class 10 Maths chapter 11 to learn about two dimensional figures areas. All solutions at Tiwari Academy are expertly solved by professional Maths teachers, ensuring accuracy and clarity. Chapter 11 of Grade 10 Maths NCERT covers three important topics, providing students with a thorough understanding of key concepts. These solutions help in mastering the subject and preparing effectively for exams.
Class 10 Maths Chapter 11 in English for CBSE Board
Class 10 Maths Exercise 11.1 in English
Class 10 Maths Chapter 11 in English for State Boards
Class 10 Maths Chapter 11 Exercise 11.1
Class 10 Maths Chapter 11 Exercise 11.2
Class 10 Maths Chapter 11 in Hindi Medium
Class 10 Maths Exercise 11.1 in Hindi
Course for Class 10 Maths Chapter 11 Areas Related to Circles
Area of sectors and segments of a circle. Problems based on areas and perimeter /circumference of the above said plane figures. (In calculating area of segment of a circle, problems should be restricted to central angle of 60°, 90° and 120° only.
NCERT Solutions for Class 10 Maths Chapter 12 – Surface Areas and Volumes
There are a total of five exercises in Class 10 Maths chapter 12. Learn how to find the surface area of shapes like cuboids, cones, spheres, cylinders and hemispheres in Class 10 Maths Chapter 12. Tiwari Academy’s solutions provide all the necessary information, making it easy for students to understand and solve these problems effectively. Perfect for thorough exam preparation and concept mastery.
Class 10 Maths Chapter 12 in English for CBSE Board
Class 10 Maths Exercise 12.1 in English
Class 10 Maths Exercise 12.2 in English
Class 10 Maths Chapter 12 in English for State Boards
Class 10 Maths Chapter 12 Exercise 12.1
Class 10 Maths Chapter 12 Exercise 12.2
Class 10 Maths Chapter 12 Exercise 12.3
Class 10 Maths Chapter 12 in Hindi Medium
Class 10 Maths Exercise 12.1 in Hindi
Class 10 Maths Exercise 12.2 in Hindi
Class 10 Maths Chapter 12 Surface Areas and Volumes Syllabus
Surface areas and volumes of combinations of any two of the following: cubes, cuboids, spheres, hemispheres and right circular cylinders/cones.
NCERT Solutions for Class 10 Maths Chapter 13 Statistics
All the exercises of Class 10 Maths chapter 13 are explained in Hindi and English Medium. The NCERT textbook for Class 10 Mathematics Chapter 13, Statistics, covers key topics such as cumulative frequency, cumulative frequency distribution, drawing cumulative frequency curves and cumulative frequency graphs. These concepts are explained in detail to help students understand and apply statistical methods effectively in problem-solving and exam preparation.
Class 10 Maths Chapter 13 in English for CBSE Board
Class 10 Maths Exercise 13.1 in English
Class 10 Maths Exercise 13.2 in English
Class 10 Maths Exercise 13.3 in English
Class 10 Maths Chapter 13 for State Boards
Class 10 Maths Chapter 13 Exercise 13.1
Class 10 Maths Chapter 13 Exercise 13.2
Class 10 Maths Chapter 13 Exercise 13.3
Class 10 Maths Chapter 13 Exercise 13.4
Class 10 Maths Chapter 13 Exercise 13.5
Class 10 Maths Chapter 13 in Hindi Medium
Class 10 Maths Exercise 13.1 in Hindi
Class 10 Maths Exercise 13.2 in Hindi
Class 10 Maths Exercise 13.3 in Hindi
Curriculum for Class 10 Maths Chapter 13 Statistics
Mean, median and mode of grouped data (bimodal situation to be avoided).
NCERT Solutions for Class 10 Maths Chapter 14 Probability
Class 10 Maths chapter 14 delves deeper into the concepts of Probability, building on the basics learned in previous classes. At the start of the chapter, students will revisit the definition of probability. Chapter 14 covers not only the core concept but also includes simple problems to enhance understanding and application, making it easier to grasp this essential topic. Perfect for strengthening exam preparation and practical problem-solving skills.
Class 10 Maths Chapter 14 in English for CBSE Board
Class 10 Maths Exercise 14.1 in English
Class 10 Maths Chapter 14 in English for State Boards
Class 10 Maths Chapter 14 Exercise 14.1
Class 10 Maths Chapter 14 Exercise 14.2
Class 10 Maths Chapter 14 Exercise 14.3
Class 10 Maths Chapter 14 Exercise 14.4
Class 10 Maths Chapter 14 in Hindi Medium
Class 10 Maths Exercise 14.1 in Hindi
Class 10 Maths Chapter 14 Probability Focus Points
Classical definition of probability. Simple problems on finding the probability of an event.
Preparation of Mathematics in Class 10 Study
The solved examples help students to get a clear idea of the concepts given in exercises. Our experts have created exercises solutions that are simplified to learn according to the given examples. It is made as per the latest 2024-25 CBSE Syllabus and Marking scheme.
Class 10 Maths solution for the first and second term are given here for new curriculum which are prescribed by the NCERT – National Council of Educational Research and Training (https://ncert.nic.in/).
How to study Class 10 Maths using NCERT Solutions?
Find the latest NCERT Solutions for Class 10 Maths, updated for the 2024-25 exams, right here. A well-organized study plan using NCERT Solutions is key to mastering Class 10 Mathematics. Regular practice, consistency and a clear understanding of fundamental concepts are essential for exam success. Follow this structured study plan, stay committed and you’ll be well-prepared to ace your Class 10 Maths board exams. Here’s a step-by-step guide to help you achieve top scores in your exams.
- Step 1: Understand the Syllabus, Gather Resources like Books and Study Material.
- Step 2: Start with Basics, use NCERT Solutions and Take Notes of Important Terms.
- Step 3: Focus on Regular Practice, Self-Assessment and Seek Clarification.
- Step 4: Practice Time Management, Stay Healthy, make Revision and Review of course.
- Step 5: Maintain the practice time daily for Maths revision during Final Exam Preparation.
Step 1: Understand the Syllabus, Gather Resources like Books and Study Material.

Step 2: Start with Basics, use NCERT Solutions and Take Notes of Important Terms.
 Start by thoroughly reading each chapter in the Class 10 NCERT Mathematics textbook. Focus on grasping the fundamental concepts and principles. Ensure you maintain a balance between learning new concepts, practicing problems and reviewing previous topics. After completing a chapter, solve the examples and exercises provided in the textbook. Use NCERT Solutions to verify your answers, understand the correct solutions and clear any doubts. As you study, make concise notes of important formulas, theorems and key points. These notes will be invaluable for quick revision and preparing for exams efficiently.
Start by thoroughly reading each chapter in the Class 10 NCERT Mathematics textbook. Focus on grasping the fundamental concepts and principles. Ensure you maintain a balance between learning new concepts, practicing problems and reviewing previous topics. After completing a chapter, solve the examples and exercises provided in the textbook. Use NCERT Solutions to verify your answers, understand the correct solutions and clear any doubts. As you study, make concise notes of important formulas, theorems and key points. These notes will be invaluable for quick revision and preparing for exams efficiently.Step 3: Focus on Regular Practice, Self-Assessment and Seek Clarification.

Step 4: Practice Time Management, Stay Healthy, make Revision and Review of course.

Step 5: Maintain the practice time daily for Maths revision during Final Exam Preparation.

What should be my revision strategy before the Class 10 Maths exam?
An effective revision strategy before the Class 10 Maths exam involves revisiting all important concepts and formulas, focusing on chapters with high weightage. Start by reviewing your notes, solved examples and important formulas regularly. Time management is crucial, so divide your revision time to cover both strong and weak areas. Prioritise practicing difficult topics to build confidence in those areas.
Solving sample papers and previous years’ question papers under exam conditions is an excellent way to finalise your preparation. Focus on solving questions with accuracy and speed, and revisit any mistakes to avoid repeating them in the exam. The key to a successful revision is consistency and focus on weak areas, with adequate breaks for relaxation.
What types of questions are asked in Class 10 Maths board exam?
The Class 10 Maths board exam typically includes a variety of question types, such as multiple-choice questions (MCQs), short-answer questions and long-answer questions. The questions test both conceptual understanding and application skills, with a mix of theoretical problems and real-life scenarios. Some questions are directly based on NCERT exercises, while others require deeper analysis and problem-solving skills.
Application-based questions are often designed to test ability to apply concepts in practical situations, especially in topics like Trigonometry, Algebra and Geometry. The paper also includes case-study-based questions that require interpreting data and solving problems based on it. Time management and clarity of concepts are key to answering these questions effectively.
Which is the best book for Class 10 Maths board exam preparation?
The NCERT textbook for Class 10 Maths is the primary book for both Basic and Standard courses, essential for thorough board exam preparation. It serves as the best reference book, clarifying all concepts likely to be tested in the exam. Since the board exam question paper is strictly based on the NCERT textbook, it is crucial to practice this book thoroughly to achieve better scores.
To prepare for CBSE board exams, focus on these five main key points:
- Use Class 10 Maths NCERT textbook on the latest syllabus only.
- Solve previous years’ like questions from 10th Maths NCERT.
- Create and follow a structured practice timetable for Maths.
- Concentrate on NCERT textbooks for 10th Mathematics to learn fundamental concepts.
- Regularly revise the previous exercises to be confident in learning.
What is the difference between Basic and Standard Maths in Class 10?
The difference between Basic and Standard Maths in Class 10 lies in the difficulty level of the exam. Standard Maths is designed for students who wish to pursue Mathematics in higher studies, covering advanced concepts and problem-solving techniques. It includes more complex questions and application-based problems, which require a deeper understanding of the subject.
On the other hand, Basic Maths is for students who do not intend to continue studying Maths after Class 10. It has a simpler syllabus and easier questions compared to Standard Maths. Both options allow students to score well, but Standard Maths prepares students for future academic pursuits involving Maths, while Basic Maths focuses on essential concepts without much complexity.
How can I remember all the formulas in Class 10 Maths?
To remember all the formulas in Class 10 Maths, it’s important to focus on regular practice and revision. Creating formula charts and flashcards can be helpful in quick revision. Write down the formulas and place them in areas where you frequently study, allowing for constant reinforcement. Visual learning techniques like mind maps and diagrams can also aid in retention.
Regularly solving problems using these formulas will help reinforce them in your memory. Instead of memorising formulas mechanically, understand their derivations and applications. This understanding will make it easier to recall them during the exam. Repeating this process daily will ensure that you retain the key formulas effectively.
How to Simplify Learning Class 10 Maths?
CBSE aims to offer a balanced mix of easy and challenging questions to assess all types of students. The Class 10 Maths paper provides a good opportunity to score well, though it can be slightly difficult to achieve the highest marks. So, CBSE Class 10 Maths Exam is neither too easy nor to tough.
Follow the points given here to make your Maths learning easy in Class 10:
- Understand Fundamentals: Understand the basic concepts and go through the examples given before each exercise and then move to solve Exercises.
- Daily Practice: Regular Practice makes class 10 Maths more comfortable and enhance familiarity with mathematical topics and skill.
- Practice with Graphs: Use graphs papers, in chapter 3, to get solutions, draw diagrams in chapter 6, 7 and other chapters like areas related to circle and surface areas and volumes.
- Ask Questions: Always clarify doubts with teachers to avoid confusion. Students can ask question through Discussion Forum to get answers by subject experts.
- Group Discussion: Group study or group discussion is one of the best method to explore the concepts behind Maths topics. Group study provides a better way to revised and learn many new tricks to solve the same questions.
Is Class 10 Maths difficult?
Class 10 Maths can seem challenging for some students, but with the right approach and consistent practice, it becomes manageable. The syllabus covers a wide range of topics, from Algebra and Geometry to Trigonometry and Probability, which require both conceptual understanding and application skills. The key to overcoming any difficulty lies in understanding the core concepts and practicing regularly to gain confidence in solving problems.
For students who struggle with Maths, breaking down problems into simpler steps and focusing on understanding each concept thoroughly can make the subject easier. Using resources like NCERT books, sample papers and online tutorials, available on Tiwari Academy, can also provide extra support. With consistent practice and proper guidance, students can overcome the difficulty and excel in the subject.
How can I improve my problem-solving speed in Maths?
Improving problem-solving speed in Maths requires consistent practice and familiarity with different types of questions. Start by timing yourself while solving previous years’ question papers and sample papers to simulate exam conditions. Break down each problem into smaller steps to enhance efficiency. Focus on mental math techniques and shortcut methods that reduce calculation time while maintaining accuracy.
Work on your weaker areas, as struggling with tough concepts can slow you down during the exam. Regularly revising formulas and practicing quick mental calculations will help. Use mock tests to assess your performance under timed conditions and gradually, your speed and accuracy will improve as you become more familiar with various question types.
Which textbook is best for Class 10 Maths board exam preparation?
NCERT is the best study material for Class 10 Maths, making it easier for students to score 90+ marks in the board exams. After completing the NCERT textbook, it’s important to review questions from the NCERT Exemplar book for additional practice. Once done, students should move on to practice papers and extra reference books. Here are five of the best options for boosting exam preparation:
- NCERT Mathematics Textbook: NCERT books are designed to align directly with the CBSE curriculum, making them an essential study resource. This book provides a strong foundation in concepts, which is helpful for higher education.
- R.D. Sharma Mathematics for Class 10: It is Known for its extensive and exhaustive coverage of topics. It Includes a wide range of problems, from basic to challenging, helping students prepare for all types of exam questions.
- R.S. Aggarwal Mathematics for Class 10: It Focuses on enhancing conceptual understanding which is crucial for tackling application-based questions. It Offers graded exercises that help reinforce learning.
- Full Marks Mathematics for Class 10: It Contains sample papers and previous year questions which are great for exam preparation. It provides explanations that are easy to understand, making complex topics more accessible.
- Oswaal Sample Question Papers for Class 10 Maths: It Includes sample papers designed according to the latest examination patterns. It has self-assessment tools to help students evaluate their preparation level.
Which chapters are the most important for the Class 10 Maths board exam?
Some of the most important chapters for the Class 10 Maths board exam include Trigonometry, Quadratic Equations and Coordinate Geometry. These chapters frequently carry a significant weightage in the exam and often contain tricky, application-based questions. The weightage is given at the top of this page. Algebra, including Linear Equations and Polynomials, is another important area that requires a strong grasp of formulas and problem-solving techniques.
Statistics, Probability and Circles are also essential chapters, with direct and relatively straightforward questions. While all chapters are important, focusing on these high-weightage topics can help you score better. Make sure you practice multiple types of questions from these chapters to strengthen your understanding and tackle them confidently in the exam.
How to solve the toughest Chapters In Class 10 Maths?
Most of the chapters in NCERT Textbook 2024-25 are easy to solve for even an average student. Few chapters are there which is considered as difficult one by a fraction of students only. The students found difficulty in some chapters in Class 10 Maths syllabus such as:
- Chapter 6: Triangles
- Chapter 8: Trigonometry
- Chapter 9: Application of trigonometry
- Chapter 10: Circle
- Chapter 12: Surface area and volume
Doing practice well these above chapters then you can feel easier than before. Make sure you revised these difficult topics about 3-4 times before the exam.
Is Class 10 Maths easy?
Class 10 Maths can be easy or challenging depending on how well students understand the concepts and practice regularly. For students who focus on the NCERT textbook, which is the foundation of the CBSE syllabus, the subject becomes more manageable. The key is to pay attention to each chapter, practice the problems thoroughly and clear any doubts as they arise. With concepts like algebra, geometry and trigonometry, consistency in solving examples helps build confidence.
On the other hand, some topics like mensuration and probability may seem difficult but with regular practice and understanding, they can be simplified. Utilising extra resources such as NCERT Exemplar and practice papers will help reinforce learning. In conclusion, Class 10 Maths is not inherently hard; it just requires dedication and proper study techniques. With the right approach and continuous effort, students can excel in the subject and score well in their board exams.
How can I score 90+ marks in Class 10 Maths?
To score 90+ marks in Class 10 Maths, consistent practice and a deep understanding of concepts are crucial. Start by thoroughly completing the NCERT book, as most questions in the board exams are based on its content. Focus on understanding the reasoning behind each formula and solution instead of rote learning. Practice solving previous years’ papers and sample papers within the time limit to get comfortable with the exam pattern and time management.
Additionally, identify the chapters where you are weak and devote extra time to mastering those areas. Use reference books for extra practice, especially for tricky problems. Revision should be a regular part of your study plan. Take mock tests to evaluate your performance and focus on improving your problem-solving speed and accuracy to maximise your score.
Are the standard of CBSE 10th Maths Papers little bit higher than the usual school papers?
The question papers in CBSE Board exams are design in such a way, it is good for all type of students. The pattern of 10th Standard Board Examination is very simple to do and very easy to understand. But most of the people may misguide you a fear unnecessarily and do practice all the syllabus thoroughly, and you definitely score optimum marks in Class 10 Board Exam.
Qualities of Class 10 Maths Standard Question Paper:
- CBSE papers are designed to test students on the entire syllabus. They include a variety of problem types, from basic to higher-order thinking questions.
- The CBSE often emphasizes application-based and conceptual questions, which require a deeper understanding of mathematical concepts and their real-world applications.
- The marking schemes in CBSE exams are strict and detailed, with specific steps needing to be followed to score full marks. If schools be lenient in their marking, then it will lead to students finding CBSE papers tougher.
What is the importance of the NCERT book for Class 10 Maths board exams 2024-25?
The NCERT book for Class 10 Maths is considered the backbone for board exam preparation. It provides a clear and structured explanation of concepts aligned with the CBSE syllabus. Each chapter is designed to build a solid foundation in mathematical concepts, which is essential for problem-solving in board exams. Additionally, most questions in the board exam 2024-25 are directly or indirectly based on NCERT exercises, making it a critical resource for scoring well.
Moreover, the NCERT book includes various examples and practice exercises that help students understand complex problems step by step. It follows a simple yet comprehensive language that ensures clarity in concepts. Regular practice from the NCERT book helps students develop the analytical and reasoning skills required for the board exams. It also ensures students are well-versed with the format of the exam, increasing their confidence.