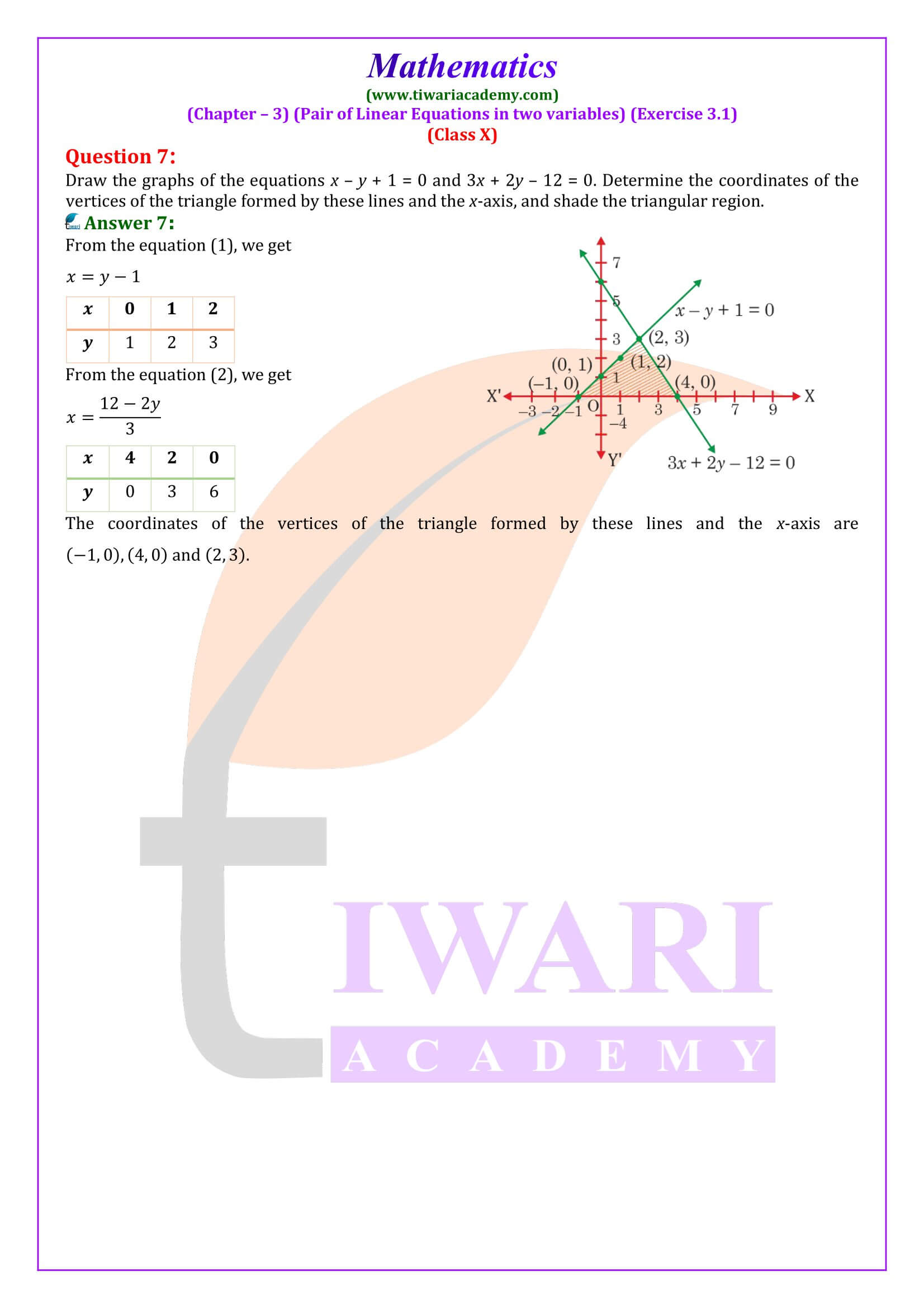
Class 10 Maths Exercise 3.1 Solutions
10th Maths Exercise 3.1 in Hindi
Class 10 Maths NCERT Book Download
Class 10 Maths Chapter 3 Solutions
Class 10 Maths NCERT Solutions
Class 10 all Subjects NCERT Solutions
NCERT Solutions for class 10 Maths Chapter 3 Exercise 3.1 in Hindi and English Medium prepared and updated for session 2024-25. The solutions of questions are modified and revised as per the new NCERT textbooks issued for board examination.
| Class: 10 | Mathematics |
| Chapter 3: | Exercise 3.1 |
| Topic Name: | Linear Equations in two variables |
| Content Type: | Images, Text and Videos |
| Session: | Academic Year 2024-25 |
| Medium: | English and Hindi Medium |
NCERT Solutions for class 10 Maths Chapter 3 Exercise 3.1

10th Maths Ex. 3.1 solution pair of linear equations in two variables in Hindi Medium and English Medium. According to new curriculum, the syllabus for board exams is reduced. That is why many chapters and exercises are deleted from the textbooks published by NCERT. This page contains the solutions of 10th Maths exercise 3.1 given in new NCERT book.
Uttar Pradesh Board, Prayagraj also implemented NCERT Textbooks for their students, so these CBSE Solutions are useful UP Board students also. Get here the UP Board Solutions for class 10 Maths Chapter 3 Exercise 3.1 in Hindi Medium.
All the contents on Tiwari Academy are free. Download these solutions or View in Video Format free for CBSE board, Gujrat board and UP Board students using NCERT Books. Download Offline Apps of CBSE Solutions based on latest CBSE Syllabus.
NCERT Solutions for class 10 Maths Chapter 3 Exercise 3.1 in English medium and Hindi Medium are given here updated for all board. To download solutions visit at NCERT Solutions for class 10 Maths Chapter 3 main page. Join the Discussion Forum to share your knowledge with the other users.
Important Questions on Class 10 Chapter 3 for Practice
- Find the value of k for which pair of linear equations 3x + 2y = –5 and x – ky = 2 has a unique solution. [Answer: k≠-2/3]
- Express y in terms of x in the expression 3x – 7y = 10. [Answer: y = (3x-10)/7]
- Find three consecutive numbers such that seven times the smallest number may be equal to three times the sum of the other two. [Answer: 9, 10, 11]
- If 2x + 5y = 4, write another linear equation, so that lines represented by the pair are coincident. [Answer: 4x+10y=8]
- Jamila sold a table and a chair for ₹1050, thereby making a profit of 10% on the table and 25% on the chair. If she had taken a profit of 25% on the table and 10% on the chair, she would have got ₹1065. Find the cost price of each. [Answer: Cost of table = ₹500, cost of chair = ₹400]
- Check whether the graph of the pair of linear equations x + 2y – 4 = 0 and 2x + 4y – 12 = 0 is intersecting lines or parallel lines. [Answer: parallel lines]
QUESTIONS FROM CBSE BOARD PAPERS
1. A number consists of three digits whose sum is 17. The middle are exceeds the sum of the other two by 1. If the digits be reversed, the number is diminished by 369. Find the number. [Answer: 692]
2. If the lines 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then find value of k. [Answer: k=15/4]
3. After covering a distance of 30 km at a uniform speed, there is some defect in a train engine and therefore, its speed is reduced to 4/5 to its original speed. Consequently, the train reaches its destination late by 45 minutes. Had it happened after covering 18 km more, the train would have reached 9 minutes earlier than it did. Find the speed of the train and the length of the journey. [Answer: Speed = 30 km/h, length of journey = 120 km]
4. If we draw lines of x = 2 and y = 3 what kind of lines do we get? [Answer: intersecting lines]
5. A 90% acid solution is mixed with a 97% acid solution to obtain 21 litres of a 95% solution. Find the quantity of each of the solutions to get the resultant mixture. [Answer: 6 litres 90% solutions and 15 litres 97% solutions].
Important Questions 10th Maths Exercise 3.1
Romila went to a stationery shop and purchased 2 pencils and 3 erasers for Rs 9. Her friend Sonali saw the new variety of pencils and erasers with Romila, and she also bought 4 pencils and 6 erasers of the same kind for Rs 18. Represent this situation algebraically.
Let us denote the cost of 1 pencil by x and one eraser by y. Then the algebraic representation is given by the following equations:
2x + 3y = 9 …(1)
4x + 6y = 18 …(2)
If two linear equation in two variables are intersecting at one common point. How many solutions are their?
The common point on both the lines, there is one and only one solution for the pair of linear equations in two variables.
How many solutions are their for two parallel lines?
Parallel lines never intersect each other. So, there is no solutions for these system of linear equations.
If the graph of two linear equations are coincide, how many solutions are there?
If the lines are coincident, then every point on the line is the solutions for the equations. There are infinitely many solutions.
Download Offline Apps and ask your doubts in Discussion Forum. You can ask questions related to NIOS board or CBSE Board NCERT Books.
How many questions are there in Class 10 Maths Exercise 3.1?
There are in all 7 questions in exercise 3.1 of class 10th mathematics chapter 3 (Pair of linear equations in two variables) and all questions of this exercise are important.
How many examples are based on exercise 3.1 of class 10th mathematics?
Only 3 examples (examples 4, 5 and 6) are based on exercise 3.1 (chapter 3 Pair of linear equations in two variables) of class 10th mathematics and all three examples are important. Also all three examples are of different type.
Which questions of exercise 3.1 class 10th Maths can easily do?
Students can easily do few questions like Question 2, 3 and 4 of exercise 3.1 (chapter 3 Pair of linear equations in two variables) of class 10th mathematics.
Which questions of exercise 3.1 class 10th Math are difficult?
Students find Q 1, 5, 6 and 7 of exercise 3.1 (chapter 3 Pair of linear equations in two variables) of class 10th mathematics difficult. These questions need more practice to learn better.