NCERT Solutions for Class 10 Maths Chapter 2 Exercise 2.1

For Exercise 2.1 in class 10 Maths Chapter 2 (Polynomials), to prepare effectively for exams, you should first focus on understanding the graphical representation of polynomial zeroes. This exercise involves interpreting graphs to identify the number of zeroes of a given polynomial. Spend time practicing how to read graphs and understand the relationship between the x-axis and the zeroes of different types of polynomials. Focus on identifying how linear, quadratic and cubic polynomials behave graphically, as this will be key to answering these questions. Review past problems and ensure you can quickly determine zeroes based on visual cues.

Work on speed and accuracy. Time yourself while solving multiple problems of this type, ensuring that you can correctly identify zeroes in a given time frame. This exercise is likely to appear in exams where quick graphical interpretation is needed. Practice sketching simple polynomial graphs yourself to build intuition and ensure you know how changes in the coefficients of polynomials affect the graph’s shape and the location of zeroes.

Class 10 Maths Ex. 2.1 Polynomials / Bahupad Hindi Medium and English Medium download in PDF format or View in Video Format free for new academic session 2024-25. All the contents are free to use for all users without any long or password. UP Board students can take benefits of these solutions as they are using NCERT Books for their course. Explanation of all the questions are in Hindi and English medium with examples. Videos related to 10th Maths Ex. 2.1 solutions are also given below. Offline Solutions Apps 2024-25 are updated according to new CBSE Syllabus 2024-25 for Gujrat Board, CBSE / Uttarakhand & UP Board students studying NCERT Books 2024-25. Download (Exercise 2.1) in PDF form or use it online without download. Enjoy all the contents free of cost and use without any restrictions as all the contents on Tiwari Academy is free to use.

NCERT Solutions for class 10 Maths Chapter 2 Exercise 2.1 Polynomials in Hindi and English medium to use it online or download in PDF. If you find any difficulty or error in these solutions, please inform us. We are here to help you in education without any charges.

1. Polynomial: If x is a variable, n is a natural number and a0, a1, a2, a3, ………. an are real numbers, then p(x) = an x^n + a^n-1. X^x-1 + ……… + a1 x + a0, (an ≠ 0) is called a polynomial in x.
2. Polynomials of degree 1, 2 and 3 are called linear, quadratic and cubic polynomials respectively.
3. A quadratic polynomial is an algebraic expression of the form ax² + bx + c, where a, b, c are real numbers with a ≠ 0.
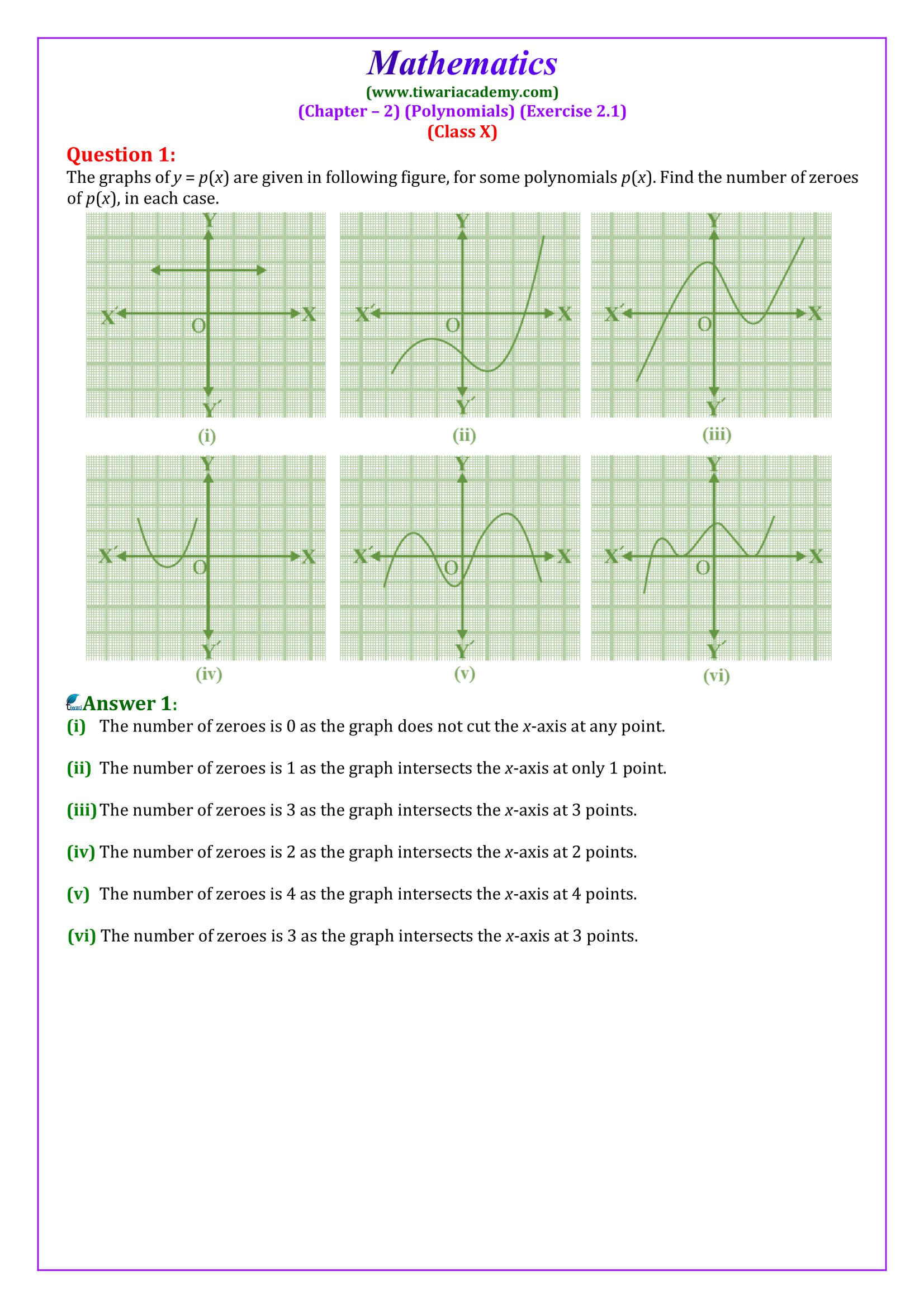
4. Zeroes of a polynomial p(x) are precisely the x – coordinates of the points where the graph of y = p(x) intersects the x–axis, i.e., x = a is a zero of polynomial p(x) if p(a) = 0.
5. Division Algorithm states that given any polynomials p(x) and g(x), there exist polynomial q(x) and r(x) such that: p(x) = g(x). q(x) + r(x) ; g(x) ≠ 0, [where either r(x) = 0 or degree r(x) < degree g(x)] 6. A polynomial can have at most the same number of zeroes as the degree of the polynomial. 7. Relationship between zeroes and coefficients of a polynomial. If m and n are zeroes of p(x) ax² + bx + c (a ≠ 0), them Sum of zeroes = m + n = – b/a, Product of zeroes = mn = c/a 8. If m, n are zeroes of a quadratic polynomial p(x), then p(x) = k[x² – (sum of zeroes) x + product of zeroes] or p(x) = k [x² – (m + n)x +mn]; where k is any non-zero real number. 9. Graph of linear polynomial p(x) = ax + b is a straight line. (i) If one zero of a quadratic polynomial p(x) is negative of the other, then coefficient of x = 0. (ii) If zeroes of a quadratic polynomial p(x) are reciprocal of each other, then co-efficient of x² = constant term.

1. What will be the number of zeroes of a linear polynomial p(x) if its graph (i) passes through the origin. (ii) doesn’t intersect or touch x-axis at any point? [Answer: (i) 1, (ii) 0]
2. Find the quadratic polynomial whose zeroes are 5 + 2√3 and 5 – 2√3. [Answer: x² – 10x + 13]
3. For what value of p, is – 4 a zero of the polynomial x² – 2x – (7p + 3)? [Answer: 3]
4. If one zero of p(x) = 4x² – (8k2 – 40k) x – 9 is negative of the other, find values of k. [Answer: k = 0, 5]

5. What number should be added to the polynomial x² – 5x + 4, so that 3 is a zero of polynomial so obtained? [Answer: 2]
Download NCERT Books and Offline apps based on new CBSE Syllabus. Ask your doubts and share your knowledge with your friends and other users through Discussion Forum.