by Tiwari Academy
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry in English and Hindi Medium for CBSE 2024-25 Exams. NCERT Class 10 Math Textbook chapter 8 is revised as per the CBSE Mathematics books published for Academic Session 2024-25.
Class 10 Maths Chapter 8 Exercise 8.1 Solutions
Class 10 Maths Chapter 8 Exercise 8.2 Solutions
Class 10 Maths Chapter 8 Exercise 8.3 Solutions
10th Maths Chapter 8 Solutions for State Boards
| Class: 10 | Mathematics |
| Chapter 8: | Introduction to Trigonometry |
| Content Type: | Text, Videos and PDF |
| Contents: | NCERT Textbook Solutions |
| Session: | CBSE 2024-25 |
| Medium: | Hindi and English medium |
Class 10 Maths Chapter 8 Introduction to Trigonometry Solution
Class 10 Maths Chapter 8 Solutions are updated for current academic session 2024-25 based on NCERT Books. UP Board students are also using NCERT Textbooks for their exams now. So, they also can download UP Board Solutions for Class 10 Maths Chapter 8 Solutions in Hindi Medium from this page. Solutions are given in videos format also describing in English and Hindi.
NCERT Solutions and Offline apps for UP Board and CBSE Board are also given free to download. Download Offline as well as Online Apps based on updated NCERT Solutions based on latest NCERT books 2024-25. Revision books are also available to download. Description, history and identities related to Trigonometry is given below.
10th Maths Chapter 8 Solutions
NCERT Solutions for class 10 Maths Chapter 8 Introduction to Trigonometry exercises from 8.1 to 8.3 are given to use online of download in PDF format free. These solutions are in Hindi and English Medium format. If you have any doubt, please visit to Discussion Forum to ask your doubts.
Historical Facts!
1. The creator of trigonometry is said to have been the Greek Mathematician Hipparchus of the 2nd century BC.
2. The word Trigonometry which means triangle measurement is credited to Bastholoman Pitiscus (1561-1613).
3. The first use of the idea of ‘sine’ can be found in the work of ‘Aryabhatiyam’ of Aryabhata in 500 AD. Aryabhata used the word Ardha-jya for the half-chord, which was shortened to Jya or Jiva in due course. When the Aryabhatiyam was translated into Arabic, the word Jiva was retained. It was further translated into ‘Sinus’, which means curve in Latin. The word ‘Sinus’ also used as sine was first abbreviated and used as ‘sin’ by an English professor of astronomy Edmund Gunter (1581-1626).
4. The origin of the terms ‘Cosine’ and ‘tangent’ was much later. The cosine function arose from the need to compute the sine of the complementary angle. Aryabhata called it Kotijya. The name cosinus originated with Edmund Gunter. In 1674, another English mathematician Sir Jonas Moore first used the abbreviated notation ‘cos’.
Trigonometric Identities
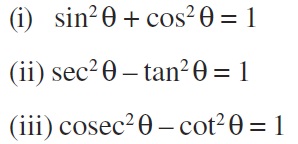
Trigonometric Ratios
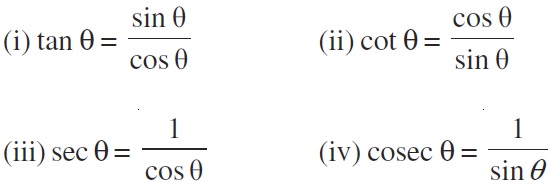
How many exercise wise questions are there in class 10 Maths chapter 8?
There are 4 exercises in class 10 math chapter 8 Introduction to Trigonometry.
In first exercise (Ex 8.1), there are in all 11 questions.
In second exercise (Ex 8.2), there are in all 4 questions.
In third exercise (Ex 8.3), there are 5 questions.
So, there are in all 20 questions in class 10 math chapter 8 Introduction to Trigonometry.
There are in all 15 examples in class 10 math chapter 8 Introduction to Trigonometry.
Examples 1, 2, 3, 4, 5 are based on Ex 8.1.
Examples 6, 7, 8 are based on Ex 8.2.
Examples 12, 13, 14, 15 are based on Ex 8.3.
What are the important examples from chapter 8 class 10 math?
Examples given in NCERT books are always important for CBSE exams. Examples 3, 4, 5, 7, 8, 10, 11, 13, 14 and 15 of chapter 8 (Introduction to Trigonometry) of class 10 math are the important examples from exam point of view. In exam questions can come from these examples.
Which are the main topics students go through in chapter 8 of class 10th Mathematics?
In chapter 8 Introduction to Trigonometry of class 10th math, Students will study:
1) Trigonometric Ratios.
2) Trigonometric Ratios of Some Specific Angles.
3) Trigonometric Identities.
This chapter is very interesting. Also this chapter is completely new for students.
Why is chapter 8 of Class 10th Maths important?
Chapter 8 (Introduction to Trigonometry) of 10th Math is important because there is a chapter in class 11th math named Trigonometric functions and chapter 8 (Introduction to Trigonometry) of 10th Math works as a base for that chapter. Also from exam point of view chapter 8 (Introduction to Trigonometry) of 10th Math is very important. Every year 7-8 marks questions come from this chapter.
What do you learn about Trigonometry in Class 10 Maths Chapter 8?
Trigonometry is the oldest branch of mathematics. This concept was first used by Aryabhata in Aryabhatiyam in 500 A.D. Trigonometry is a word consisting of three Greek words: Tri-Gon-Metron. ‘Tri’ means three, ‘Gon’ means side and ‘Metron’ means measure. So, trigonometry is the study related to the measure of sides and angles of a triangle in particular, right triangles (in CBSE class 10).
How can I score more that 90% in class 10 Maths Chpater 8 Trigonometry?
To score well in trigonometry, we should practice hard the entire chapter 8 in 10th Maths. Specially exercise 8.4 needs more time to spend for solving the questions based on identities. All the parts of question 5 of exercise 8.4 asked in exams frequently.
Is there any application of trigo as a tool in astronomy for Class 10 Mathematics 8th Chapter?
Trigonometry is used in astronomy to determine the position and the path of celestial objects. Astronomers use it to find the distance of the stars and planets from the Earth. Captain of a ship uses it to find the direction and the distance of islands and light houses from the sea. Surveyors use to map the new lands.
What is the objective of Chapter 8 in Class 10 Maths Trigonometry?
Objective of Class 10 Trigonometry:
Identifying the opposite side, adjacent side and hypotenuse of right triangle with respect to given angle A. Defining the six rations (sine, cosine, tangent, secant. cosecant and cotangent) related to the sides of a right angled triangle. Finding the values of trigonometric rations of a given right angled triangle. Finding the values of trigonometry rations of some standard angles (0, 30, 45, 60 and 90) in degrees. Using complementary angles and applying it into trigonometric identities to prove another identities.
