by Tiwari Academy
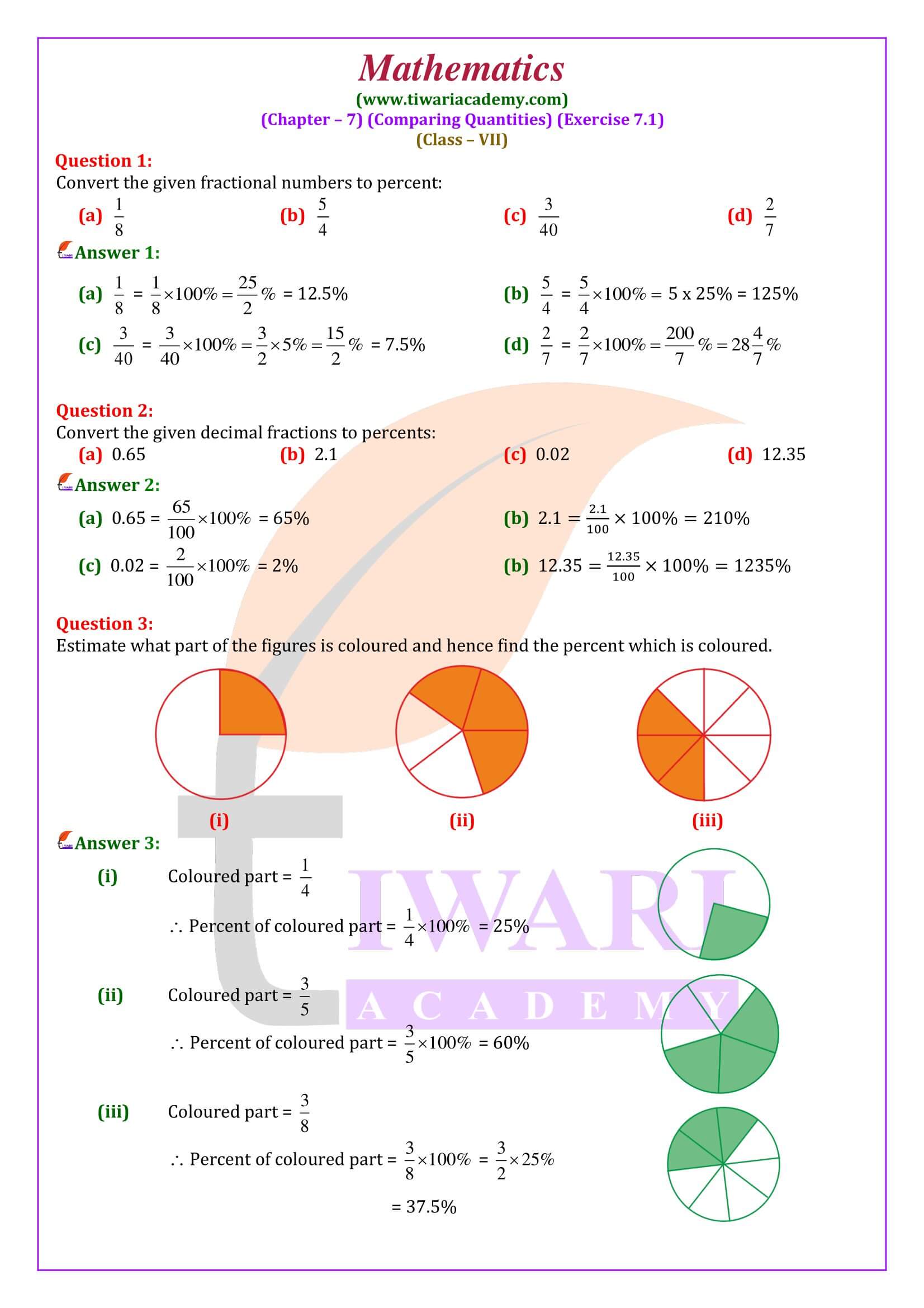
NCERT Solutions for Class 7 Maths Chapter 7 Exercise 7.1 Comparing Quantities in Hindi and English Medium for session 2024-25. The question answers and explanation of ex. 7.1 class 7th math are revised following the latest NCERT textbooks issued for CBSE 2024-25 exams.
NCERT Class 7 Maths Exercise 7.1 Solution in Hindi and English Medium
Class 7 Maths Chapter 7 Exercise 7.1 Solution
Solutions are prepared by subject experts using step by step calculation. In class 7 mathematics NCERT exercise 7.1, questions are based on the concept of percentage and its application. Here we will learn to convert a simple number or fraction into percentage or percentage to fraction.
Class 7 Maths App in English
Class 7 Maths Chapter 7 Exercise 7.1 Solution in Videos
Class 7 Maths App in Hindi Medium
| Class: 7 | Mathematics |
| Chapter: 7 | Exercise: 7.1 |
| Topic: | Comparing Quantities |
| Content Mode: | Text, Images and Videos |
| Academic Session: | CBSE 2024-25 |
| Medium: | Hindi and English Medium |
Class 7 Maths Exercise 7.1 Extra Questions
Convert each of the following fractions into a percentage: (i) 33/100, (ii) ¾ (iii) 7/25 (iv) 11/40
We have:
(i) 33/100 = {(33/100) x 100} % = 33%
(ii) ¾ = {(3/4) x 100} % = 75%
(iii) 7/25 = {(7/25) x 100} % =28%
(iv) 11/40 = {(11/40) x 100} % = 27(1/2) %
Express each of the following as a ratio: (i) 17 % (ii) 72 % (iii) 12.5 % (iv) 225 %
We have, (i) 17 % = 17/100 = 17 : 100.
(ii) 72 % = 72/100 = 18/28 = 18 : 25.
(iii) 12.5 % = 12.5/100 = 125/1000 = 1/8 = 1 : 8.
(iv) 225 % = 225/100 = 9/4 = 9 : 4
Convert each of the following into a fraction: (i) 35 % (ii) 56 % (iii) 37.5 % (iv) 140 %
We have:
(i) 35 % = 35/100 = 7/20
(ii) 56 % = 56/100 = 14/25
(iii) 37.5 % = 37.5/100 = 375/1000 = 3/8
(iv) 140 % = 140/100 = 7/5
Convert each of the following ratios into a percentage: (i) 14 : 25 (ii) 5 : 6 (iii) 111 : 125 (iv) 8 : 5.
We have:
(i) 14 : 25 = 14/25 = (14/25) x 100 % = 56 %
(ii) 5 : 6 = 5/6 = (5/6) x 100 % = 83(1/3) %
(iii) 111 : 125 = 111/125 = (111/125) x 100 % = 88.8 %
(iv) 8 : 5 = 8/5 = (8/5) x 100 % = 160 %
Convert each of the following into a decimal fraction: (i) 36% (ii) 5.4%
We have:
(i) 36% = 36/100 = 0.36
(ii) 5.4% = 5.4/100 = 54/1000 = 0.054
Convert each of the following decimal into a percentage: (i) 0.8 (ii) 0.36
We have:
(i) 0.8 = (0.8 x 100) % = 80 %
(ii) 0.36 = (0.36 x 100) % = 36 %
Percentage
The word ‘per cent’ is derived from Latin phrase ‘per centum’ meaning ‘per hundred’. Per cent is represented by the symbol % and means hundredths too.
Example:
Suppose Ashish obtains 87 marks out of 100 in English. Then, we say that he has obtained 92 per cent marks in English.
Similarly, if there is a box containing 100 toys, out of which 15 toys are defective, we say that 15 per cent of the toys in the box are defective.
To Convert a Fraction into a Percentage
RULE: In order to convert a fraction into a percentage multiply the fraction by 100 and put the per cent sign %.
Class 7 Maths Exercise 7.1 Important Questions
How do I turn a number into a percentage?
To convert a number into percent multiple it by 100 and then add the percent sign. These examples convert the numbers 23 and 158 to percent’s. To convert a number with a decimal into percent, multiply it by 100 and add the percent sign.
What is percentage formula?
Formula to Calculate Percentage
The Percentage Formula is given as, Percentage = (Value ⁄ Total Value) × 100.
How do I calculate a percentage between two numbers?
First: work out the difference (increase) between the two numbers you are comparing. Then: divide the increase by the original number and multiply the answer by 100.
To Convert a Percentage into a Fraction:
RULE: To convert a percentage into a fraction, we divide it by 100 and remove the sign %.
Percentage as a Ratio: A percentage can be expressed as a ratio with its second term 100 and first term equal to the given percentage.
To Convert a Given Ratio into a Percentage:
RULE: First convert the given ratio into fraction, and then multiply the fraction by 100 and put the per cent sign %.
To Convert a Given Percentage in Decimal Form:
RULE: First convert the given percentage into fraction and then put the fraction into decimal form.
To Convert a Given Decimal into a Percentage:
RULE: Multiply the given decimal by 100 and put the per cent sign %
