NCERT Solutions for Class 8 Maths Chapter 6 Exercise 6.2 Cube and Cube Roots in Hindi and English Medium updated for 2024-25 exams. Get the revised solutions of ex. 6.2 of 8th mathematics based on latest NCERT textbooks issued for new academic session 2024-25.
8th Maths Exercise 6.2 Solution in Hindi and English Medium
| Class: 8 | Mathematics |
| Chapter: 6 | Exercise: 6.2 |
| Topic Name: | Cube and Cube Roots |
| Medium: | Hindi and English |
| Academic Session: | CBSE 2024-25 |
| Content Type: | Text and Vidoes Format |
Class 8 Maths Chapter 6 Exercise 6.2 Solution
Mathematics for 8th NCERT book chapter 6 Ex. 6.2 Cube and Cube Roots in Hindi and English Medium updated for academic session 2024-25. All the solutions are available in PDF and Videos format free to use online or download without any login or password. NCERT textbook Question answers are explained step by step in easy way. Do you know that the cubes of even numbers are even and the cubes of odd numbers are odd.

Cube Roots
The cube root of a number x is that number cube gives x. We denote the cube root of x by ∛x.
- Since (2 x 2 x 2) = 8, we have ∛8 = 2.
- Since (5 x 5 x 5) = 125, we have ∛125 = 5.
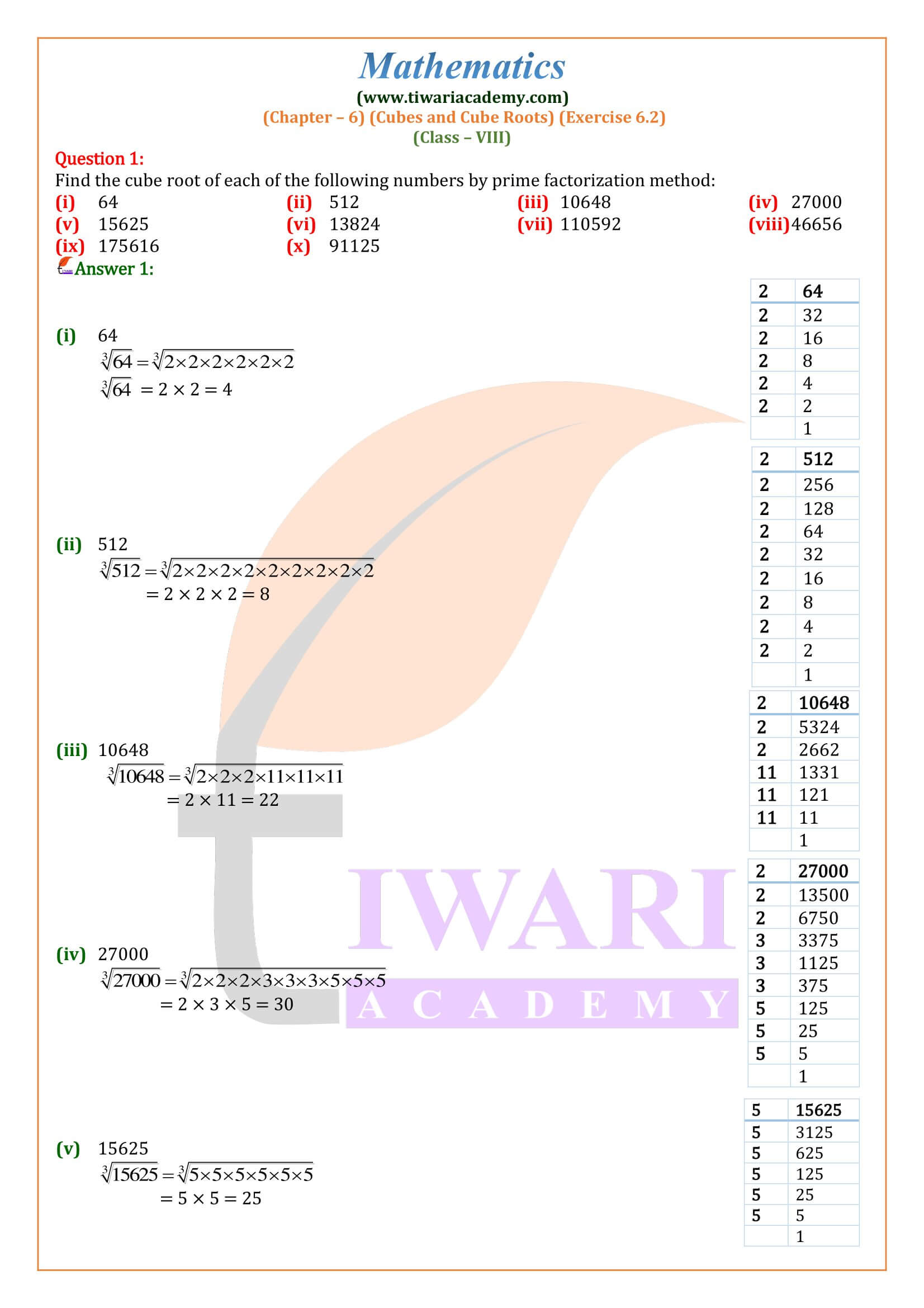
Method of Finding the cube Root of a Given Number by Factorisation:
- Express the given number as the product of primes.
- Make groups in triplets of the same prime.
- Find the product of primes, choosing one from each triplet.
- This product is the required cube root of the given number.
Evaluate ∛216.
By prime factorisation, we have
216 = 2 x 2 x 2 x 3 x 3 x 3
= (2 x 2 x 2) x (3 x 3 x 3)
∛216 = (2 x 3) = 6.
Cube Root of a Negative Perfect Cube
Let a be a positive integer.
Then, (-a) is a negative integer.
We know that (-a)³ = -a³.
Find the cube root of (-1000).
Resolving 1000 into ∛ (-1000) = -∛1000.
1000 = 2 x 2 x 2 x 5 x 5 x 5
∛1000 = (2 x 5) = 10.
∛-1000 = -∛1000 = -10.
Cube Root of Product of Integers
We have, ∛ab = ∛a x ∛b
Evaluate ∛ (125 x 64)
We have:
∛ (125 x 64) = ∛ (125) x ∛ (64)
∛ (5 x 5 x 5) x ∛ (4 x 4 x 4) = 5 x 4 = 20
Cube Root of a Rational Number
We have, ∛ (a/b) = ∛a / ∛b
What do you learn about a Perfect Cube in exercise 6.2 of 8th Maths?
If class 8th Mathematics exercise 6.2, we study that a perfect cube is a number that is the cube of an integer.
Some examples of perfect cubes are 1, 8, 27, 64.
How do you find the cube root of 729 using the tricks of exercise 6.2 of class 8 Maths?
The cube root of 729, denoted as ∛729, is a value which after getting multiplied by itself thrice gives the original value.
This is the usual definition of the cube root of a number.
Let us say, ‘n’ is the value of 3√729, then
n × n × n
= n³
= 729.
= 9 x 9 x 9
So, ∛729 = 9