What is a Linear equation?

The solutions of linear equations in two variables may include Graphical Method, Algebraic Method like Substitution, Elimination, Cross-Multiplication, etc. Methods. We can find many solutions for an equation of two variables (tow unknown variables) if we have only one equation. So, when we have two variables, we need at least two independent equations to get a unique solution. One way to find the values of unknown quantities is by using the Model method. In this method, rectangles or portions of rectangles are often used to represent the unknowns.

What is Substitution Method for solving Linear Equation?

This method is useful for solving a pair of linear equations in two variables where one variable can easily be written in terms of the other variable. The step by step method is as follows:

1. In one of the equations, express one variable in terms of the other variable. Say y in terms of x.
2. Substitute the value of y obtained in step 1 in the second equation.
3. Simplify the equation obtained in step 2 and find the value of x.
4. Substitute the value of x obtained in step 3 in either of the equations and solve it for y.
5. Check the obtained solution by substituting the values of x and y in both the original equations.

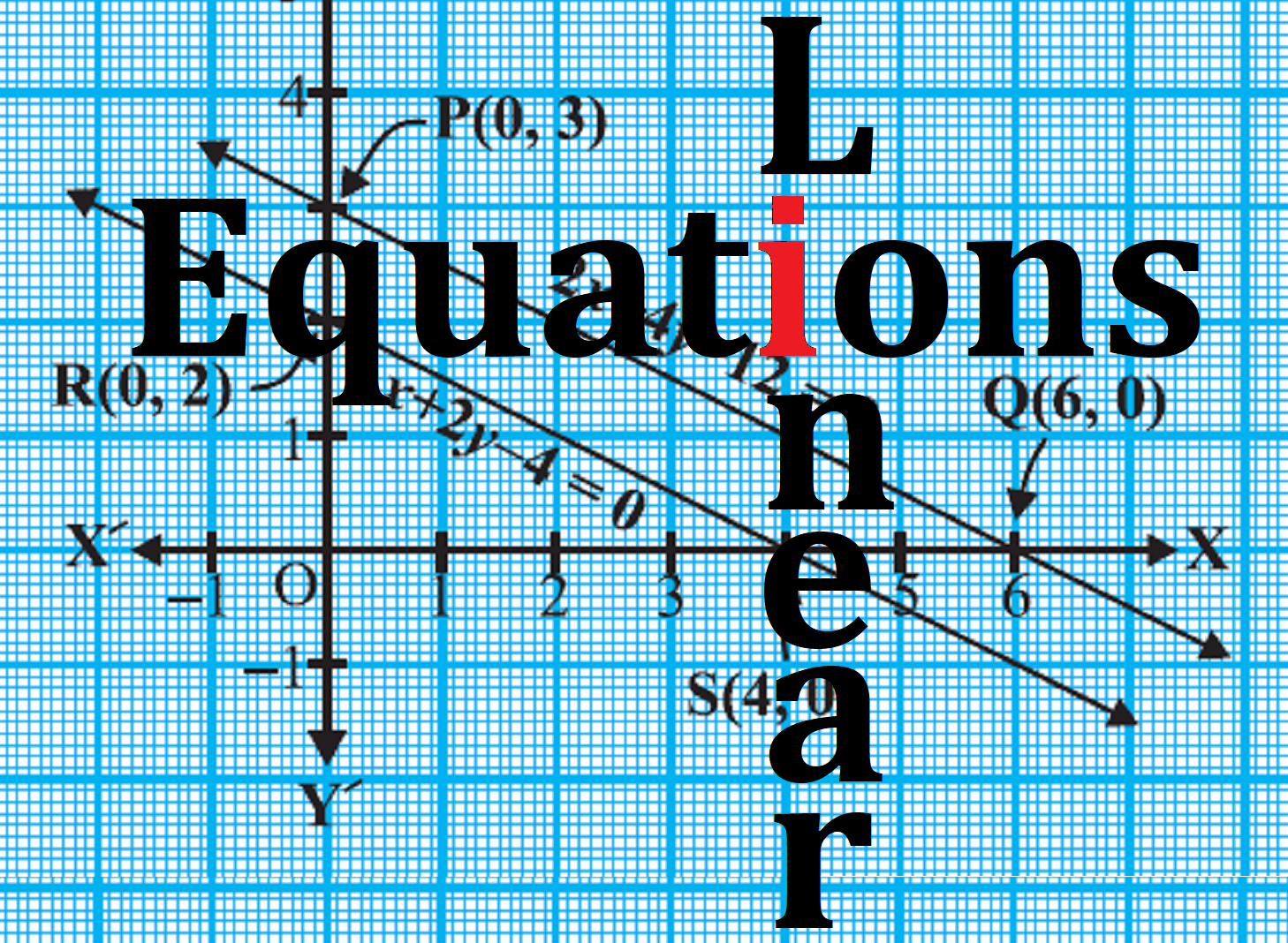
How is Graphical Method used to solve Linear Equations?

When we have a pair of equations, they represent lines in the same plane. So, if we have two lines on the same plane. When two lines are drawn in the same plane, only one of the following three situations is possible:

• The two lines may intersect at one point.
• The two lines may not intersect, i.e., they are parallel.
• The two lines may be coincident. (actually, both are same)

What is the working of Elimination Method to solve Linear Equations?

In this method, first, we eliminate (remove) one of the two variables by equating its coefficients. This gives a single equation which can be solved to get the value of the other variable. To understand this method, let us consider it step wise:

• Write both the equations in the form of ax + by = c.
• Make the coefficients of one of the variables say x, numerically equal by multiplying each equation by suitable real numbers.
• If the variable to be eliminated has the same sign in both equations, subtract the two equations to get an equation in one variable. If they have opposite sign, then add.
• Solve the equation for the remaining variable.
• Substitute the value of this variable in any one of the original equations and find the value of the eliminated variable.

History of Linear Equations

Around 4000 years ago, the people of Babylon knew how to solve a simple 2X² system of linear equations with two unknowns. Around 200 BC, the Chinese published that “Nine Chapters of the Mathematical Art,” they displayed the ability to solve a 3X^3 system of equations. In ancient time, people frequently use a simple equation of type ax + b = 0 from all walks of life. The progress in linear algebra was not significant until the late 17th century.

Euler brought to light the idea that a system of equations does not necessarily have to have a solution. He recognized the need for conditions to be placed upon unknown variables in order to find a solution. The initial work did not gear up until this period mainly dealt with the concept of unique solutions and square matrices, where the number of equations matched the number of unknowns.

In the 19th century, Gauss introduced a new procedure to be used for solving a system of linear equations. His work dealt mainly with the linear equations and had yet to bring in the idea of matrices or their notations.