NCERT Solutions for Class 5 Maths Mela Chapter 10 Symmetrical Designs for Session 2025-26. It helps students understand the concept of symmetry in a simple way. The solutions explain lines of symmetry using clear examples and pictures. Each question is solved step by step for easy learning. The content follows the latest NCERT syllabus. These solutions are useful for homework and exam practice. They help students identify symmetrical shapes and patterns. This chapter builds visual thinking and confidence in mathematics.
Class 5 Maths Mela Chapter 10 Solutions
Class 5 Maths Mela Chapter 10 MCQ
Class 5 Math Magic Chapter 10 Solutions
Class 5 Maths all Chapters Solutions
Symmetrical Designs Class 5 Maths Mela Chapter 10 Solutions
Page 136
Which of the following alphabet cutouts can be made by just drawing half (½) or quarter (¼) of the letter? You can do it by drawing lines of symmetry on the letters.
Answer:
Cutouts made by just drawing half (½) and quarter (¼) of the letter are as follows:

Which of the letters have a horizontal line of symmetry?
See AnswerE, X, O have a horizontal line of symmetry.
Which of the letters have a vertical line of symmetry?
See AnswerX, T, V, O have a vertical line of symmetry.
Which letters have both vertical and horizontal lines of symmetry?
See AnswerX, O have both vertical and horizontal lines of symmetry.
Let Us Do on Page 136 Class 5 Maths Mela Chapter 10
Let Us Do
Use lines of symmetry to make paper cutouts of diya, boat, and other designs.
Look along the border of the page to find the pictures.

Answer:

Page 137
Observe the dot in the firki. Does the firki look the same after 1/4, 1/2, 3/4, and a full turn?
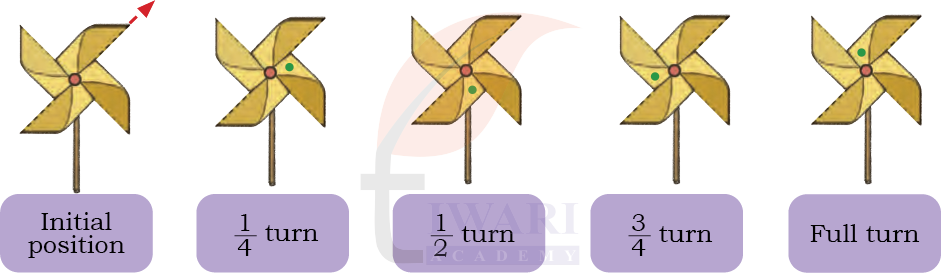
See AnswerYes, the firki looks the same at each of these turns. Just the green dot inside firki changes the position.
Page 138
Observe the letters below. Do they look the same when turned? Dots have been marked on the letters to keep track of the orientation of letters. You may also cut out the letters and fix the centre point of the letter by a nail or use a tracing paper to check if the letter looks the same when turned.
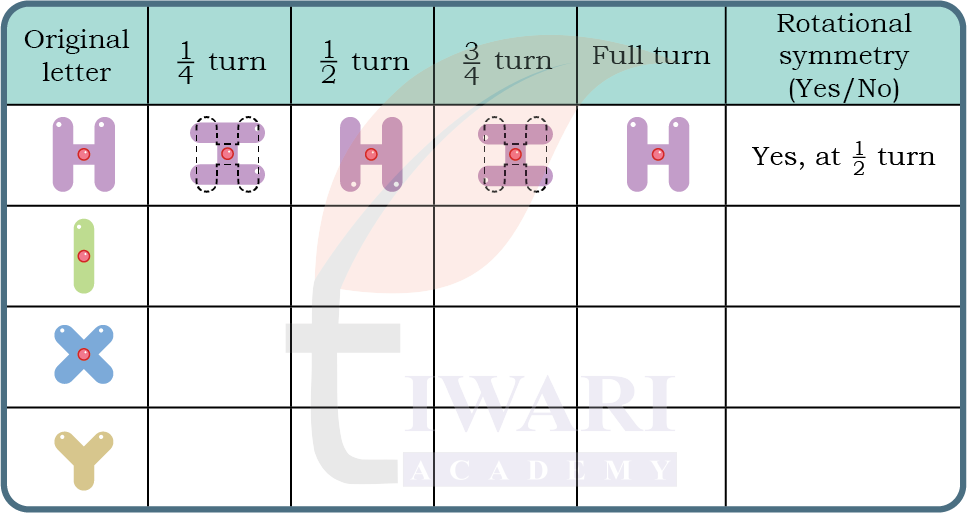
Answer:
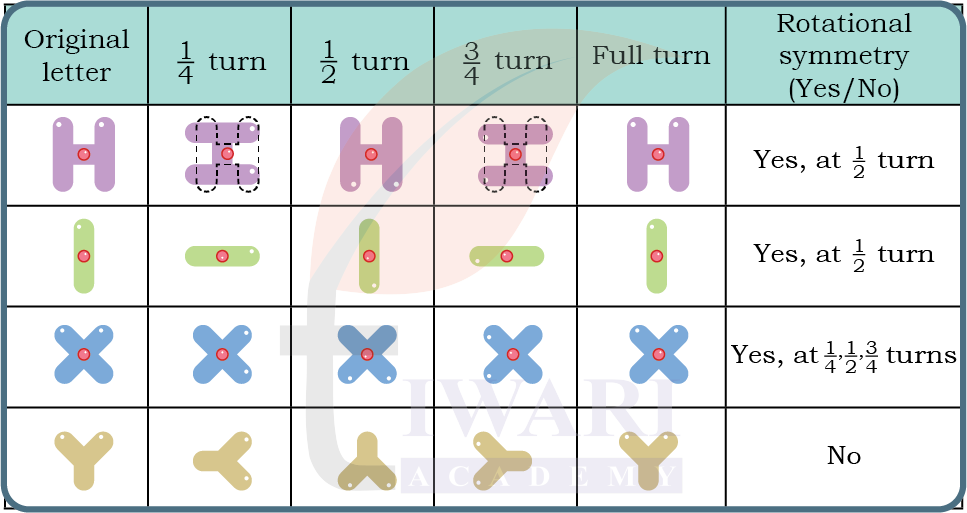
Class 5 Maths Mela Chapter 10 Page 138 Let Us Do
Page 138
Let Us Do
Find symmetry in the digits.
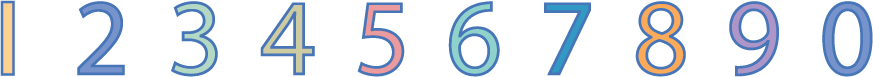
See AnswerRotational symmetry: Digit looks the same when rotated 180° (upside down).
Vertical symmetry: Digit looks the same if reflected along a vertical axis (mirror along the center).
Horizontal symmetry: Digit looks the same if reflected along a horizontal axis (mirror along the middle).
Symmetry of each digit:
0, 1 and 8 have all three symmetries(Rotational, Vertical and Horizontal)
3 has only Horizontal symmetry but does not have Rotational and Vertical symmetries.
2, 4, 5, 6, 7, 9 do not have any symmetries(Rotational, Vertical and Horizontal).
Which digit(s) have reflection symmetry?
See AnswerA digit has reflection symmetry if it can be folded along a line (vertical or horizontal) and both halves match exactly.
So, 0, 1 and 8 have reflection symmetry.
Which digit(s) have rotational symmetry?
See Answer0, 1 and 8 have rotational symmetry.
Which digit(s) have both rotational and reflection symmetries?
See Answer0, 1 and 8 have both rotational and reflection symmetries.
Now, let us look at the following numbers: II, IOOI
Do these have (a) rotational symmetry, (b) reflection symmetry or (c) both
symmetries?
See Answer(a) Rotational symmetry II and IOOI
Numbers have rotational symmetry. After rotating it by 180°, it still reads II and IOOI.
(b) A number has reflection symmetry if it can be folded in half (horizontally or vertically) and both halves are mirror images of each other.
II and IOOI: This number has reflection symmetry along a vertical axis as well. A line drawn down the middle shows that both halves mirror each other
(c) II and IOOI, we will get both rotational and reflection symmetry.
Give examples of 2-, 3-, and 4-digit numbers which have rotational symmetry, reflection symmetry, or both.
See AnswerExamples of 2-digit numbers with reflection symmetry: 11, 22, 44, 55, 88
Examples of 3-digit numbers with reflection symmetry: 101, 121, 131, 141
Examples of 4-digit numbers with reflection symmetry: 1001, 2112, 4444, 6886
Examples of 2-digit numbers with rotational symmetry: 69, 96
Examples of 3-digit numbers with rotational symmetry: 101, 181, 609
Examples of 4-digit numbers with rotational symmetry: 1001, 6009, 8008
Combination of both (if it has both types of symmetry) would be rare, but some numbers like 88 or 8008 could have both types of symmetry.
Class 5 Maths Mela Chapter 10 Designs based Questions
Page 139
Making Designs
(a) Does the design have rotational symmetry? Yes/No.

See AnswerNo the design does not have rotational symmetry.
Because the small circle on the right breaks rotational symmetry.
If we rotate the figure 180° (½ turn) or 90° (¼ turn), the circle on the right moves to a new position.
(b) Try to change the design by adding some shape(s) so that the new design looks the same after a 1/2 turn. Draw the new design in your notebook.
Answer:
See AnswerTo make the design look the same after a ½ turn, we need to balance the extra circle.
It can be done by adding a circle on the left. so that the design is symmetric around the center.
Now the top-bottom triangles and side circles are symmetric about the center so a 180° rotation preserves the design.

(c) Now try to modify or add more shapes so that the new design looks the same after 1/4 turn. Draw the new design in your notebook.
See AnswerYes, it can be done by placing identical circles in all four quadrants.
Now the design repeats itself every 90° rotation.

(d) Do the new designs have reflection symmetry? If yes, draw the lines of symmetry.
See AnswerYes, it has reflection symmetry along vertical and horizontal axes.
Class 5 Maths Mela Chapter 10 Thinking based Questions
Let Us Think
Does this design look the same after 1/2 turn?__________
Does the design look the same after 1/4 turn?__________

See AnswerYes, it looks the same after 1/2 turn.
1/2 turn means rotating the square 180°.
Opposite squares have the same color, so a 180° rotation preserves the pattern.
No, it does not look the same after a 1/4 turn.
1/4 turn means rotating the square 90°.
Adjacent squares have different colors, so a 90° rotation changes the positions of the colors.
Colour the square given in the adjoining figure using two colours so that the design looks the same after every 1/4 turn.

Answer:

How many times does this shape look the same during a full turn?
See AnswerA full turn is 360°.
If the design repeats every 1/4 turn (90°), it will appear the same at:
90°
180°
270°
So, the shap look same 3 times in a full turn.
Do these designs have reflection symmetry also? Draw the line(s) of symmetry.
Answer:
See AnswerNo, these designs do not have reflection symmetry.
Page 139
Let Us Do
Cut out squares and equilateral triangles with the same side length. These are provided at the end of the book.
Make different symmetrical designs by using these two shapes.
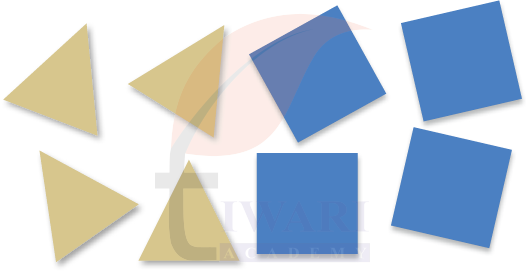
Answer:
Different symmetrical designs by using these two shapes:

Does this shape have reflection symmetry? If yes, draw its line(s) of symmetry.

See AnswerYes, it has reflection symmetry.
If we fold the shape along this vertical line, the left side and right side will match exactly.
If we fold it sideways (from top to bottom), the top side and bottom side will match exactly.
So, it has horizontal as well as vertical line of symmetry.

Does it have rotational symmetry? If yes, at which turn?
See AnswerIf we turn the shape 90°, 180°, or 270° – it does not look the same as the original.
Only after a full turn (360°) it looks the same – but that doesn’t count as rotational symmetry.
So, No rotational symmetry.
Does it have both symmetries?
See AnswerNo, it has only reflection symmetry nut not the rotational symmetry.
Now, make your designs. Sort your designs in 3 categories — designs with only rotational symmetry, designs with only reflection symmetry, and designs with both rotational and reflection symmetry.
Answer:

Page 140
Let Us Explore
Below are images of wooden blocks and a part of their prints. Match each block to its correct print by drawing a line. One is done for you.

Answer:

Page 141
Observe the pattern made by the wooden block below. We get the final print by using the block 4 times.
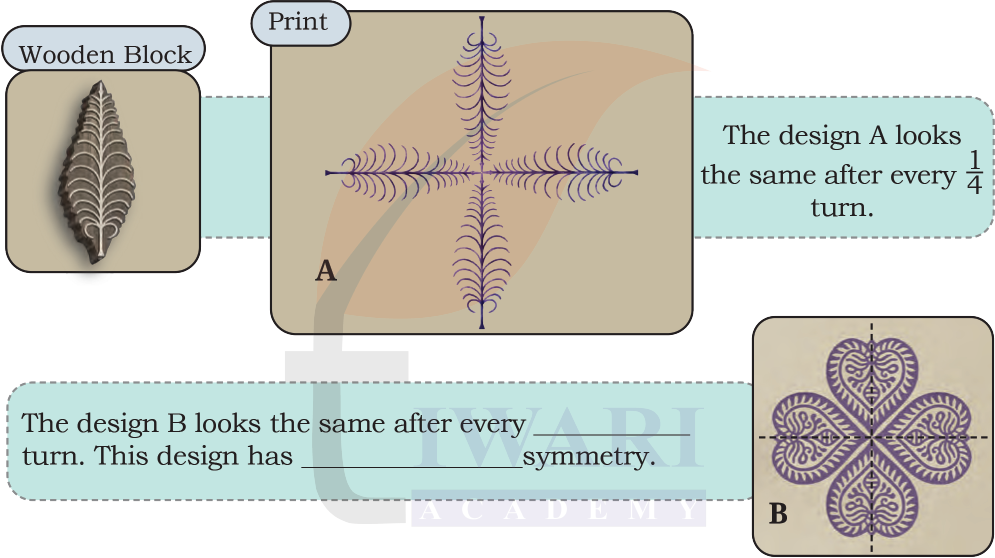
See AnswerThe design B looks the same after every 1/4, 1/2 and 3/4 turn. This design has rotational and reflection symmetry.
Page 141
Let Us Do
Observe the shapes given on the border. Which of the shapes have reflection symmetry? Put a (✓) mark on them. Put a * on the shapes that have rotational symmetry.

Answer:


