NCERT Solutions for Class 5 Maths Mela Chapter 6 The Dairy Farm

Page 70

Let Us Think

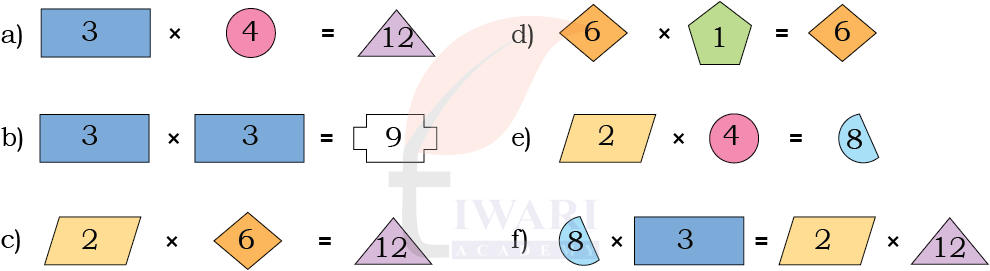
1. The given shapes stand for numbers between 1 and 24. The same shape
denotes the same number across all problems. Find the numbers hiding in all the shapes.

Answer:

2. Place the digits 2, 5 and 3 appropriately to get a product close to 100. Share your reasoning in class.

Answer:

As per the above possibilities 53 x 2 = 106 is the close to 100.

3. A dairy has packed butter milk pouches in the following manner. Find the number of pouches kept in each arrangement. One is done for you.

Answer:

4. Which number am I?
I am a two-digit number. Find me with the help of the following clues.

See SolutionLet’s find the number step-by-step:
(a) I am greater than 8.
It means I am lying in the numbers 10, 11,12,…99.
(b) I am not a multiple of 4.
So, I am not any of 12, 16, 20, 24,…., 96.
(c) I am a multiple of 9.
Multiple of 9 but not 4 (as given in (b)) and more than 9.
So, I will be a number from the set [18, 27, 45, 54, 63, 81, 90, 99] only.
(d) I am an odd number.
Removing even numbers from the result of (c), we get 27, 45, 63, 81, 99.
So, I will be one of the five numbers.
(e) I am not a multiple of 11.
Excluding the multiple of 11, we get from (d): 27, 45, 63, 81
(f) I am less than 50.
Selecting the number from the result of (e), which are less than 50: 27, 45
These numbers are not fit for clue (g) and (h). So, if we ignore clue (d), we get 18 in the process, which fulfil the conditions given in clues (g) and (h).
(g) My ones digit is even
(h) My tens digit is odd.
Therefore, the number is 18.

5. Make your own numbers.
Choose any two numbers and one operation from the grid. Try to make all the numbers between 0 and 20. For example, 2 can be formed as 4 – 2. Could you make all the numbers?
Which numbers could you not make? Is it possible to make these numbers using three numbers? You can use two operations, if needed. Which numbers between 0–20 can you get in more than one way?

See Solution0 = 4 – 4 (if we can use the same number)
1 = 5 – 4
2 = 5 – 3
3 = 36 ÷ 12
4 = 100 ÷ 25
5 = 25 ÷ 5
6 = 10 – 4
7 = 5 + 2
8 = 5 + 3
9 = 12 – 3
10 = 100 ÷ 10
11 = 36 – 25
12 = 10 + 2
13 = 25 – 12
14 = 10 + 4
15 = 25 – 10
16 = 12 + 4
17 = 12 + 5
18 = 36 ÷ 2
19 → I don’t see any way to make 19.
20 = 100 ÷ 5
So I can make all numbers except 19 (and 0 only if I cannot repeat the same number).

Page 72

Order of Numbers in Multiplication

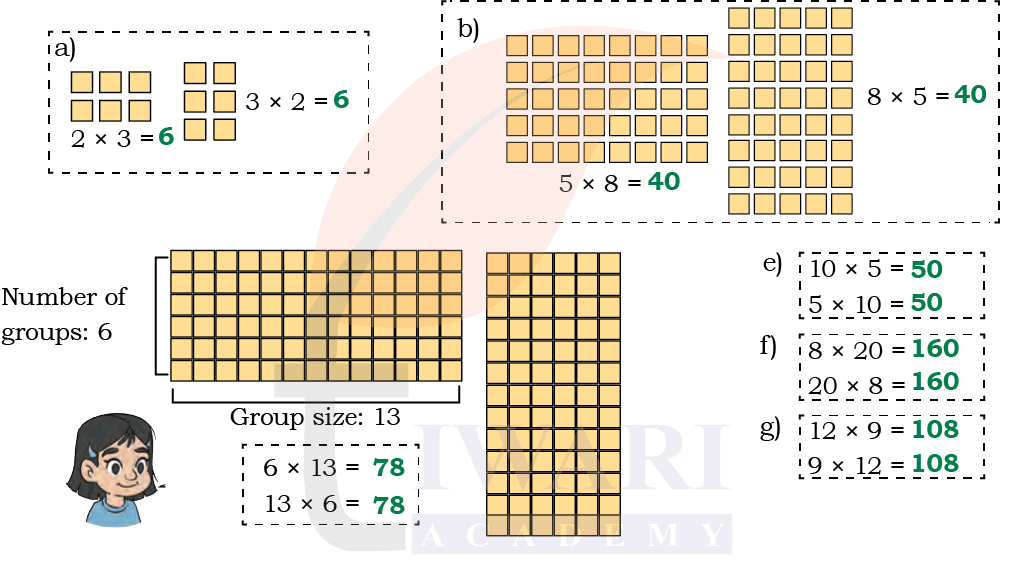
Daljeet Kaur runs a milk processing unit. She has arranged the butter packets in the following ways. Find the number of butter packets in each case. What pattern do you notice (or observe)? Discuss in class.

Answer:

Page 72

Patterns in Multiplication by 10s and 100s

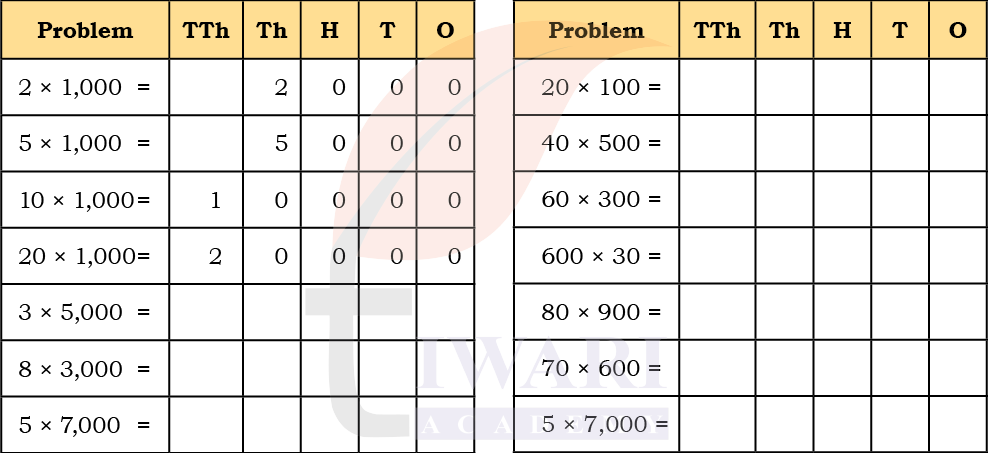
1. Let us revise multiplication by 10s and 100s.
a) 4 × 10 = _____ b) 20 × 10 = _____ c) 10 × 40 = _____ d) 10 × 10 = 100 e) 20 × 50 = ______ f) 80 × 10 = ______
g) 3 × 100 = 100 × 3 = 300 h) 8 × 100 = _____ = ______ i) 10 × 100 = _____ = _____
See Solutiona) 4 × 10 = “40” b) 20 × 10 = “200” c) 10 × 40 = “400” d) 10 × 10 = 100 e) 20 × 50 = “1000” f) 80 × 10 = “800”
g) 3 × 100 = 100 × 3 = 300 h) 8 × 100 = “100 × 8” = “800” i) 10 × 100 = “100 × 10” = “1000”

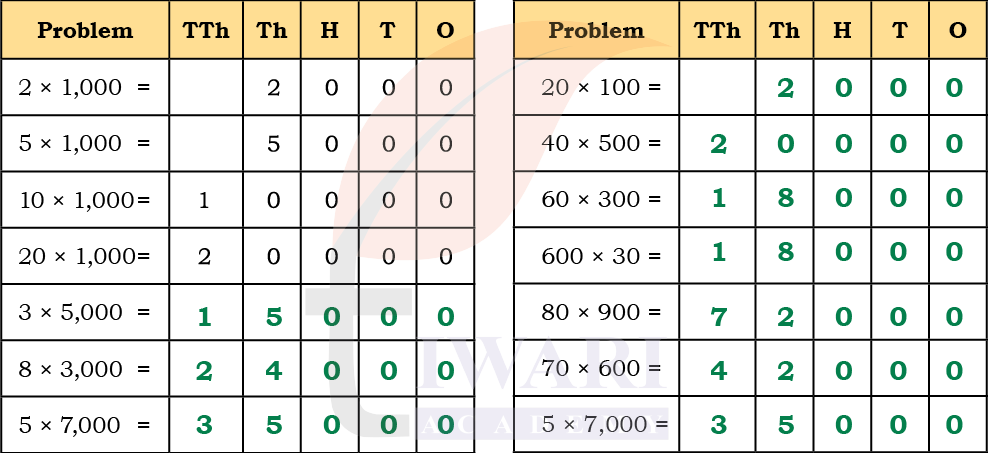
2. Find answers to the following questions. Fill in the table below and describe the pattern. Discuss in class.

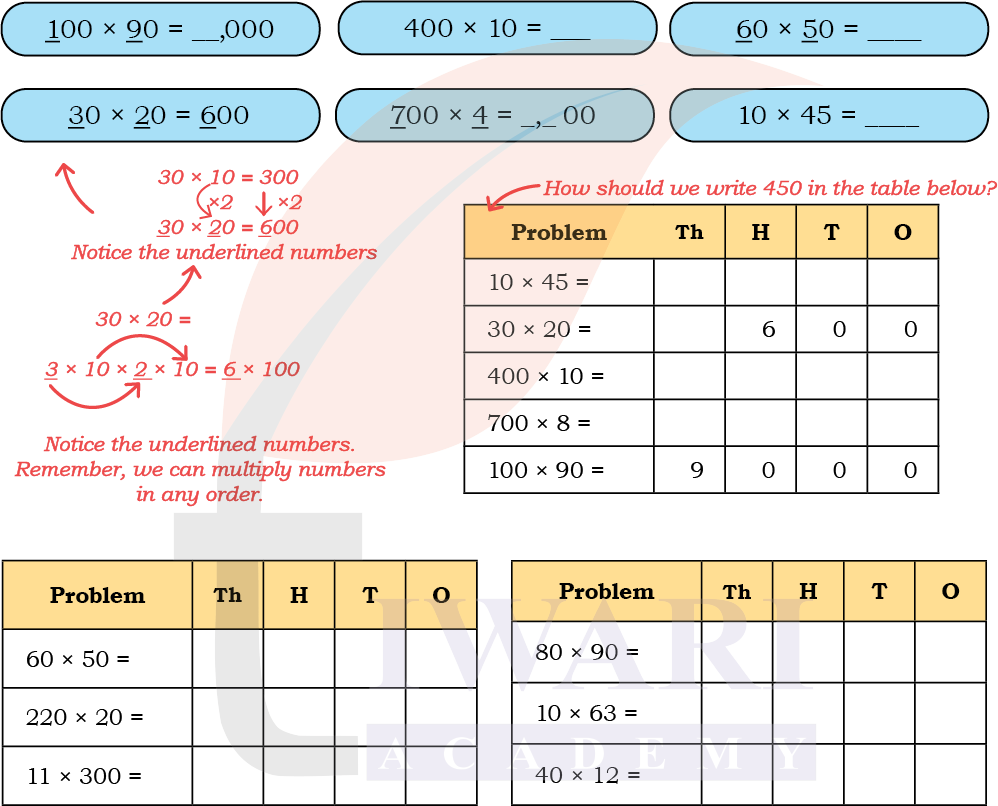
Answer:
The Pattern
When we multiply numbers that end with zeros, the non-zero digits are multiplied first.
Example: 30 × 20 → (3 × 2 = 6). Then, count the zeros (two zeros). So, answer = 600.
Classroom Discussion Example
Teacher: “What is 400 × 10?”
Student A: “4 × 1 = 4, then add three zeros → 4000.”
Student B: “In the table, 4 goes in the thousands place, rest are zeros”.
Teacher: “Good! So what’s the pattern?”
Class: “Multiply the non-zero digits first, then count the total zeros and add them”.

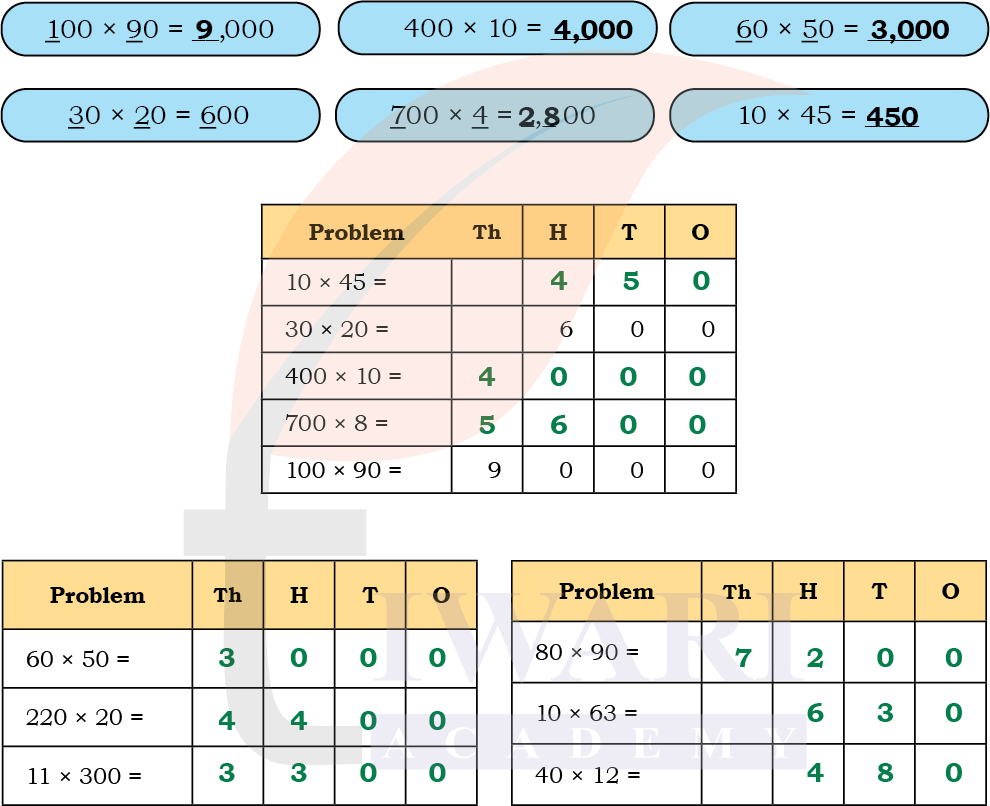
Let us fill in the table and observe the patterns.

Answer:

Page 75

Doubling and Halving

Butter packets are arranged in the following ways. Let us find some strategies to calculate the total number of packets.
This halving and doubling strategy works well when we have to multiply with numbers like 5 and 25. Discuss why?

Answer:

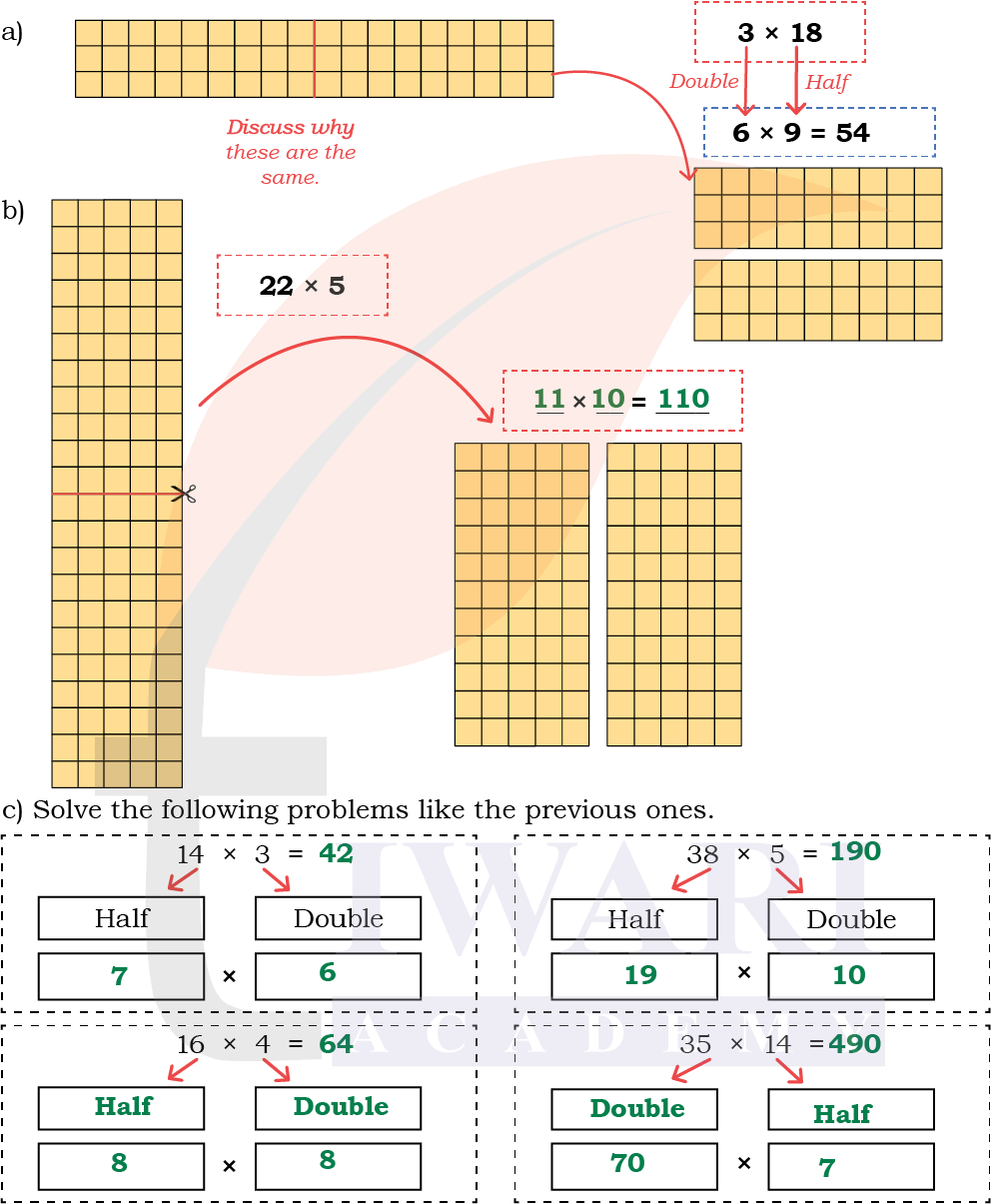
The halving and doubling strategy works so well with numbers like 5, 25, 50, etc., because these numbers have a close and simple relationship with powers of 10 (10, 100, 1000, etc.), which are the easiest numbers to multiply by.

(d) Find the product by halving and doubling either the multiplier or the multiplicand.
1) 5 × 18
2) 50 × 28
3) 15 × 22
4) 25 × 12
5) 12 × 45
6) 16 × 45
See Solution1) 5 × 18: Halve 18, Double 5 → (9 × 10) = 90
2) 50 × 28: Halve 28, Double 50 → (14 × 100) = 1,400
3) 15 × 22: Halve 22, Double 15 → (11 × 30) = 330
4) 25 × 12: Halve 12, Double 25 → (6 × 50) = 300
5) 12 × 45: Halve 12, Double 45 → (6 × 90) = 540
6) 16 × 45: Halve 16, Double 45 → (8 × 90) = 720

(e) Give 5 examples of multiplication problems where halving and doubling will help in finding the product easily. Find the products as well.
See Solution5 examples Multiplication problems:
1. 5 x 16
2. 25 x 8
3. 15 x 6
4. 50 x 18
5. 35 x 4
Using halving and doubling method to get product easily
1. 5 × 16 = (10 × 8) = 80
2. 25 × 8 = (50 × 4) = 200
3. 15 × 6 = (30 × 3) = 90
4. 50 × 18 = (100 × 9) = 900
5. 35 × 4 = (70 × 2) = 140
As we can see by using halving and doubling method it is easy to do the multiplications.

Page 76

Nearest Multiple

(a) 4 × 19

See SolutionIt is convenient to multiple 4 with 20 rather than 19. So, we multiply 4 with 20 and subtract 4 to reduce one vertical block as given in the picture.

(b) 14 × 21

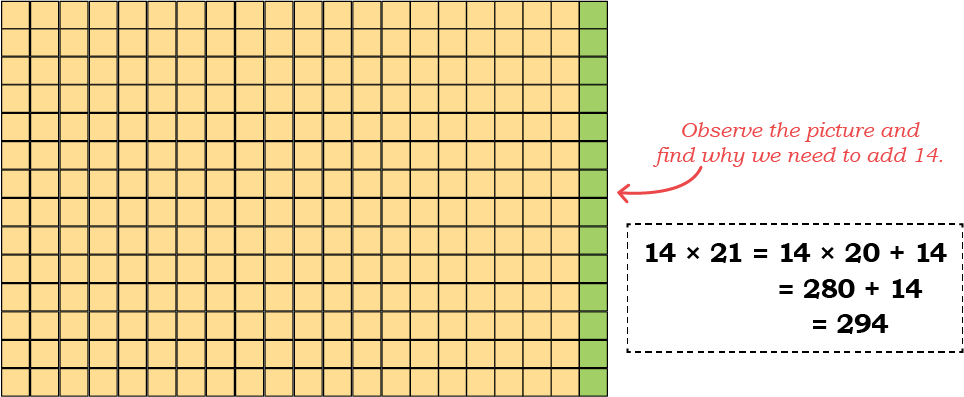
Observe the picture and find why we need to add 14.
See SolutionIt is convenient to multiple 14 with 20 rather than 21. So, we multiply 14 with 20 and add 14 to increase one vertical block as given in the picture.

(c) Give 5 examples of problems where you can use the nearest multiple to find the product easily. Find the products as well.
See Solution1. 6 × 49 = 6 x 50 – 6 = 300 – 6 = 294
2. 8 × 52 = 8 x 50 + 16 = 400 + 16 = 416
3. 13 × 19 = 13 x 20 – 13 = 260 – 13 = 247
4. 11 × 102 =11 x 100 + 22 = 1100 + 22 = 1122
5. 25 × 39 = 25 x 40 – 1 = 1000 – 25 = 975
As we can see by using nearest multiple method it is easy to get the product.

(d) Find the products of the following numbers by finding the nearest multiple.
1) 7 × 52 2) 12 × 28 3) 75 × 31
4) 99 × 15 5) 8 × 25 6) 22 × 42
See Solution1. 7 × 52 = 7 × 50 + 14 = 350 + 14 = 364
2. 12 × 28 = 12 × 30 – 24 = 360 – 24 = 336
3. 75 × 31 = 75 × 30 + 75 = 2250 + 75 = 2325
4. 99 × 15 = 15 × 100 – 15 = 1500 – 15 = 1485
5. 8 × 25 = 8 × 20 + 40 = 160 + 40 = 200
6. 22 × 42 = 22 × 40 + 44 = 880 + 44 = 924

Page 77

Let Us Solve

Use strategies flexibly to answer the following questions. Discuss your thoughts in class.
1. A school has an auditorium with 35 rows, with 42 seats in each row. How many people can sit in this auditorium?
See SolutionRows in a school auditorium = 35 rows
Seats on a each row = 42
People Sitting capacity = 35 x 42 = 1470 People.

2. Priya jogs 4 kilometres every day. How many kilometers will she jog in 31 days?
See SolutionPriya Jogs in one day = 4 kilometres
Priya will jogs in 31 day = 4 x 31 = 124 km.

3. A school has received 36 boxes of books with 48 books in each box. How many total books did the school receive in the boxes?
See SolutionTotal books boxes Received = 36
In each box books quantity = 48
Total books received by school = 36 x 48 = 1728.

4. Priya uses 16 metres of cloth to make 4 kurtas. How much cloth would she need to make 8 kurtas?
See SolutionTo make 4 kurtas Priya needs cloth = 16 metres
To Make 1 Kurta Priya need cloth = 16/4 = 4 metres
For Making 8 kurtas Priya will need cloth = 32 metres.

5. Gollappa has 29 cows on his farm. Each cow produces 5 litres of milk per day. How many litres of milk do the cow produce in total, each day?
See SolutionTotal Numbers of cows in farm = 29
Each cow daily milk production = 5 litres
Total Milk production in a day = 29 x 5 = 145 litres.

6. Maska Cow Farm has 297 cows. Each cow requires 18 kg of fodder per day. How much total fodder is needed to feed 297 cows every day?
See SolutionTotal Number of cows in the farm = 297
Per day each cow fodder Requirement = 18 Kg
Total fodder needed for 297 cows = 297 x 18 = 5346 kg

Page 79

Let Us Multiply

Answer:

Page 79

Let Us Do

1. Solve the following problems like Nida did.

Answer:

2. Solve the following problems like Kanti.
a) 94 × 5
b) 49 × 6
c) 37 × 53
d) 28 × 79
Answer:

3. Solve the following problems like John.
a) 86 × 3
b) 72 × 7
c) 94 × 36
d) 66 × 22
Answer:

4. Solve the following problems:
(a) A movie theater has 8 rows of seats, and each row has 12 seats. If half the seats are filled, how many people are watching the movie? If 3 more rows get filled, how many total people will be there?
See SolutionTotal number of rows in theater = 8
Seats in each row = 12
Total seats in the theater = 12 x 8 = 96
Number of people watching movie = 96/2 = 48
[As per the question half seats are full]
3 more rows get filled, the number of people increased
= 3 x 12 = 36
Total people = 48 + 36 = 84 people.

(b) In a test match between India and West Indies, the Indian team hit twenty-four 4s and eighteen 6s across the two innings. How many runs were scored in 4s and 6s each? 234 runs were made by running between the wickets. If 23 runs were extras, how many runs were scored by Indian team in the two innings?
See SolutionRuns from 4s: 24 fours × 4 = 96 runs
Runs from 6s: 18 sixes × 6 = 108 runs
Runs as Extras = 23
Runs from running between the wickets = 234
Total runs: 96 + 108 + 234 + 23 = 461 runs.

(c) Anjali buys 15 bulbs and 12 tube lights from Sudha Electricals. Each bulb costs ₹25 and each tube light costs ₹34. How much money should Anjali give to the shopkeeper?
See SolutionTotal Bulbs Buy = 15
Cost of one Bulb = ₹25
Cost of 15 Bulbs = ₹15 x 25 = ₹375
Number of Tube light = 12
Cost of one tube light = ₹34
Cost of 12 tube lights = ₹12 x 34 = ₹408
Total money given by Anjali to shopkeeper = ₹375 + ₹408 = ₹783.

(d) A shopkeeper sold 28 bags of rice. Each bag costs ₹350. How much money did he earn by selling rice bags?
See SolutionTotal rice bags sold = 28
Each rice bag cost = ₹350
Total Money earned by selling rice bags = 28 x ₹350 = ₹9800.

(e) A school library has 86 shelves and each shelf has 162 books. Find the number of books in the library.
See SolutionTotal Shelves in the library = 86
Number of books in each shelf = 162
Total number of books in the library = 86 x 162 = 13932.

Page 83

Let Us Solve

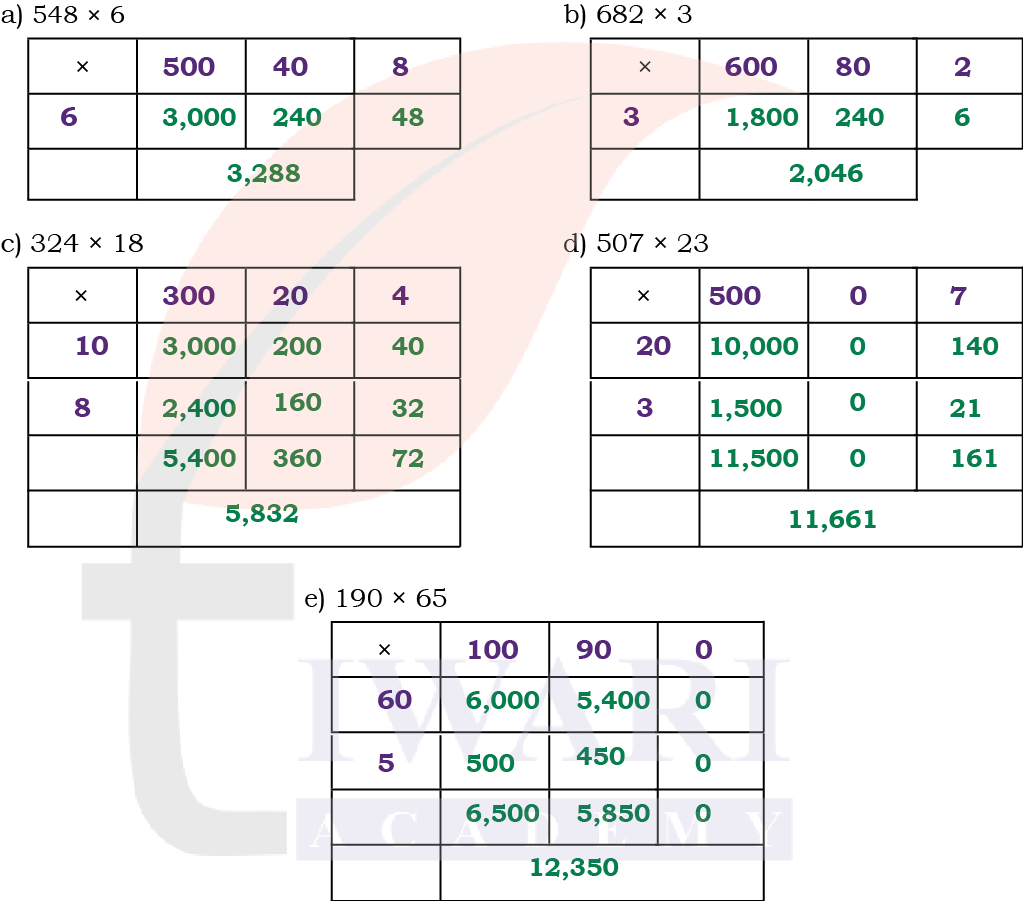
1. Solve the following problems like Nida
a) 548 × 6 b) 682 × 3 c) 324 × 18 d) 507 × 23 e) 190 × 65
Answer:

2. Solve the following problems like John.
a) 123 × 84 b) 368 × 32 c) 159 × 324
d) 239 × 401 e) 592 × 5 f) 101 × 22
Answer:

3. Let us solve a few questions like Mili’s father.

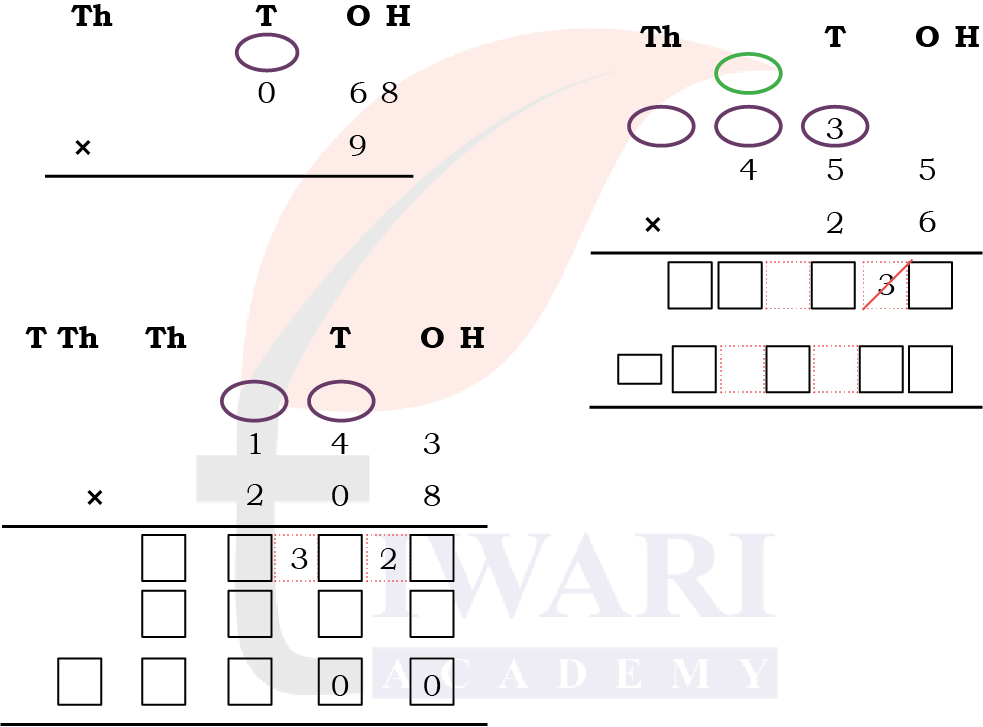
Answer:

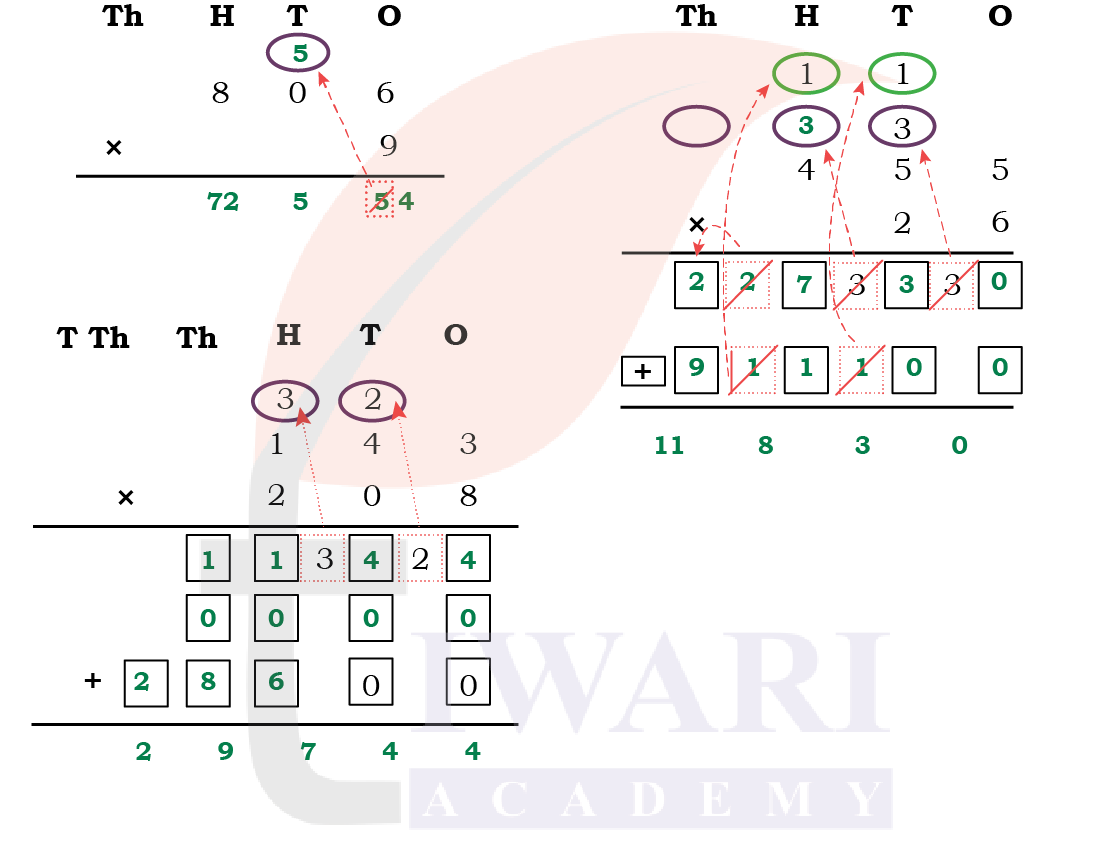
Now use Mili’s father’s method to solve the following questions.
(a) 807 × 5 (d) 450 × 38 (g) 604 × 54
(b) 143 × 28 (e) 584 × 23 (h) 112 × 23
(c) 309 × 9 (f) 302 × 13 (i) 237 × 19
Answer:

Page 86

Let Us Do

1. Identify the problems that have the same answer as the one given at the top of each box. Do not calculate.

Answer:

2. Find easy ways of solving these problems.
(a) 16 × 25
See Solution16 × 25
= (10 + 6) × (20 × 5)
= 200 + 50 + 120 + 30
= 400

(b) 12 × 125
See Solution12 × 125
= (10 + 2) × (100 × 25)
= 1000 + 250 + 200 + 50
= 1,500

(c) 24 × 250
See Solution24 × 250
= (20 + 4) × (200 + 50)
= 4000 + 1000 + 800 + 200
= 6,000

(d) 36 × 25
See Solution36 × 25
= (30 + 6) × (20 + 5)
= 600 + 150 + 120 + 30
= 900

(e) 28 × 75
See Solution28 × 75
= (20 + 8) × (70 + 5)
= 1400 + 100 + 560 + 40
= 2,100

(f) 300 × 15
See Solution300 × 15
= (300) x (10 + 5)
= 3000 + 1500
= 4,500

(g) 50 × 78
See Solution50 × 78
= (50) + (70 + 8)
= 3500 + 400
= 3,900

(h) 199 × 63
See Solution199 × 63
= (200 – 1) x (60 + 3)
= 12000 + 600 – 60 – 3
= 12,537

(i) 128 × 35
See Solution128 × 35
= (120 + 8) x (30 + 5)
= 3600 + 600 + 240 + 40
= 4,480

3. Write 5 other examples for which you can find easy ways of getting products.
See Solution1. 44 × 25
= (44 ÷ 4) × 100
= 11 × 100
= 1100
2. 8 × 375
= (10 × 375) – (2 × 375)
= 3750 – 750
= 3000
3. 99 × 28
= (100 × 28)-(1 × 28)
= 2800 – 28
= 2772
4. 125 × 16
= (125 × 8) × 2
= 1000 × 2
= 2000
5. 102 × 45
= (100 × 45) + (2 × 45)
= 4500 + 90
= 4590

4. Find the answers to the following questions based on the given information.
(a) 17 × 23 = 391 (b) 17 × 24 = _______ (c) 17 × 22 = _______
(d) 16 × 23 = _______ (e) 8 × 9 = 72 (f) 18 × 9 = _______
(g) 28 × 9 = _______ (h) 108 × 9 = _______ (i) 18 × 23 = _______
See Solution(a) 17 × 23 = 391 (given)
(b) 17 × 24 = 17 × (23 + 1)
= (17 × 23) + (17 × 1)
= 391 + 17 = 408
(c) 17 × 22 = 17 × (23 – 1)
= (17 × 23) – (17 × 1)
= 391 – 17 = 374
(d) 16 × 23 = (17 – 1) × 23
= (17 × 23) – (1 × 23)
= 391 – 23 = 368
(e) 8 × 9 = 72 (given)
(f) 18 × 9 = (10 + 8) × 9
= (10 × 9) + (8 × 9)
= 90 + 72 = 162
(g) 28 × 9 = (20 × 9) + (8 × 9)
= 180 + 72 = 252
(h) 108 × 9 = (100 × 9) + (8 × 9)
= 900 + 72 = 972
(i) 18 × 23 = (17 × 23) + (1 × 23)
= 391 + 23 = 414

Page 87

Let Us Think

1.Find the possible values of the coloured boxes in each of the following problems. The same colour indicates the same number in a problem. Some problems can have more than one answer.

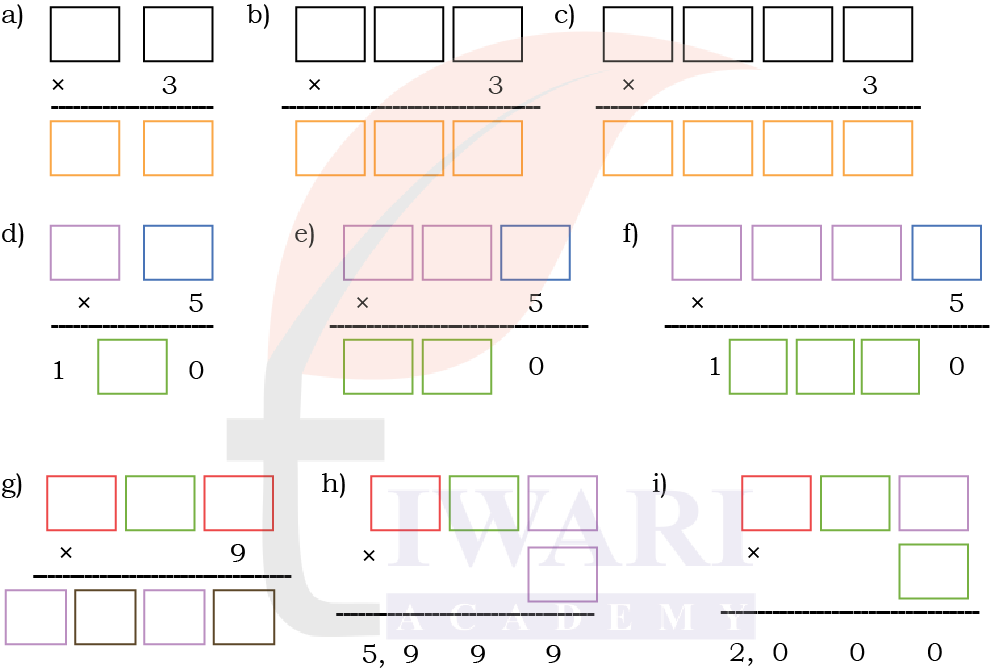
Answer:

2. Estimate the products on the left and match them to the numbers given on the right.

See Solution25 × 31 → 25 × 30 → 750
132 × 19 → 130 × 20 → 2600
101 × 11 → 100 × 10 → 1000
248 × 49 → 250 × 50 → 12500
12 × 25 → 10 × 30 → 300

Page 88

King’s Reward

Choose wisely!
Choice 1: Take 5 gold coins and double the number of coins every day for 7 days.
Choice 2: Take 3 gold coins and triple the number of coins every day for 7 days.
Choice 3: Take 1 gold coin and multiply the number of coins by 5 every day for 7 days.
Minister 1 — I will take 5 gold coins and double the number of coins every day for 7 days.
Minister 2 — I will take 3 gold coins and triple the number of coins every day for 7 days.
Minister 3 — I will take 1 gold coin and multiply the number of coins by 5 every day for 7 days.
The King gave 5 coins to Minister 1, 3 coins to Minister 2 and 1 coin to Minister 3. Which of the rewards would you have chosen? After a week, the 3 ministers were surprised at the final amount of gold coins. Guess who received the most gold coins? Calculate how much gold coins each minister received.
See SolutionChoice 1: Take 5 gold coins and double the number of coins every day for 7 days.
Day 1: 5
Day 2: 5 × 2 = 10
Day 3: 10 × 2 = 20
Day 4: 20 × 2 = 40
Day 5: 40 × 2 = 80
Day 6: 80 × 2 = 160
Day 7: 160 × 2 = 320 coins
Total = 5 + 10 + 20 + 40 + 80 + 160 + 320 = 635 coins
Choice 2: Take 3 gold coins and triple the number of coins every day for 7 days.
Day 1: 3
Day 2: 3 × 3 = 9
Day 3: 9 × 3 = 27
Day 4: 27 × 3 = 81
Day 5: 81 × 3 = 243
Day 6: 243 × 3 = 729
Day 7: 729 × 3 = 2,187 coins
Total = 3 + 9 + 27 + 81 + 343 + 729 + 2187 = 3379 coins
Choice 3: Take 1 gold coin and multiply the number of coins by 5 every day for 7 days.
Day 1: 1
Day 2: 1 × 5 = 5
Day 3: 5 × 5 = 25
Day 4: 25 × 5 = 125
Day 5: 125 × 5 = 625
Day 6: 625 × 5 = 3125
Day 7: 3125 × 5 = 15,625 coins
Total = 1 + 5 + 25 + 125 + 625 + 3125 + 15625 = 19531 coins
Minister 3 received the most gold coins: 19,531
So, I would have chosen Choice 3.

Page 89

Multiplication Patterns

1. Notice how the multiplier, multiplicand, and products are changing in
each of the following. What is the relationship of the new product with
the original product? Solve a) completely, and then predict the answers
for the rest.
a) 16 × 44 = 704
1) 8 × 88 = 704
2) 8 × 22 = 176
3) 16 × 22 = ______
4) 32 × 44 = ______
See Solution16 × 44 = 704
1) 8 × 88 = (16 ÷ 2) × (44 × 2) = 704
2) 8 × 22 = (16 ÷ 2) × (44 ÷ 2) = 704 ÷ 4.
Here, 8 × 22 = 176.
704 ÷ 4 = 176.
3) 16 × 22 = (16) × (44 ÷ 2) = 704 ÷ 2 = 352
4) 32 × 44 = (16 × 2) × (44) = 704 × 2 = 1,408.

Relationship: If you multiply one number by “a” and divide the other number by “a”, the product remains the same.
So when both are halved, product is divided by 4.

b) 12 × 32 = 384
1) 6 × 16 = ______
2) 24 × 16 = ______
3) 24 × 64 = ______
4) 12 × 16 = ______
See Solution12 × 32 = 384
1) 6 × 16 = (12 ÷ 2) × (32 ÷ 2) = 384 ÷ 4 = 96
2) 24 × 16 = (12 × 2) × (32 ÷ 2) = 384 × (2/2) = 384 × 1 = 384
3) 24 × 64 = (12 × 2) × (32 × 2) = 384 × 4 = 1,536
4) 12 × 16 = (12) × (32 ÷ 2) = 384 ÷ 2 = 192.

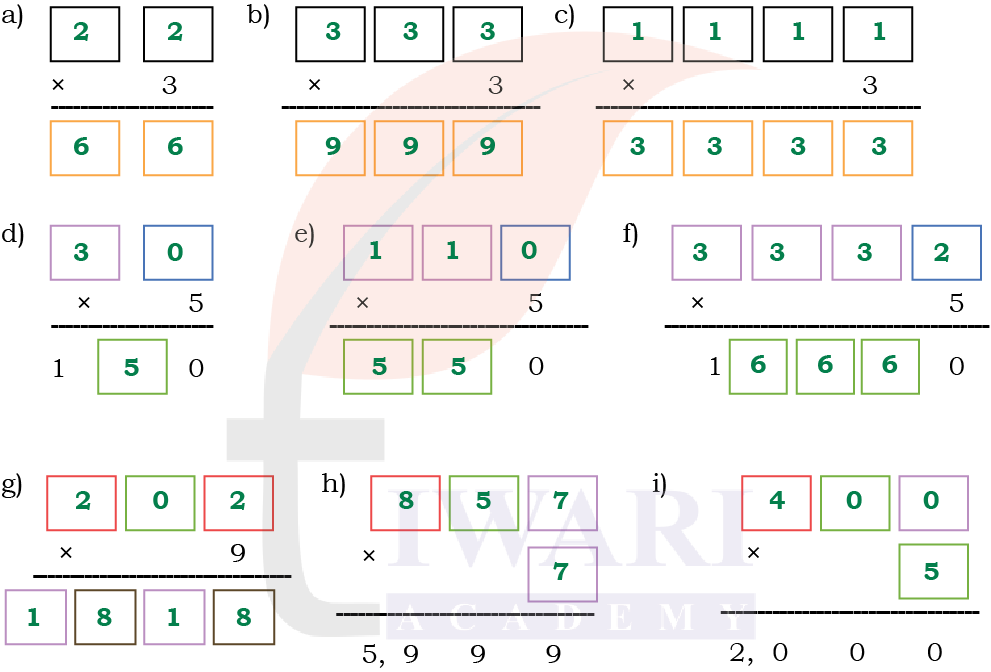
2. Observe and complete patterns:

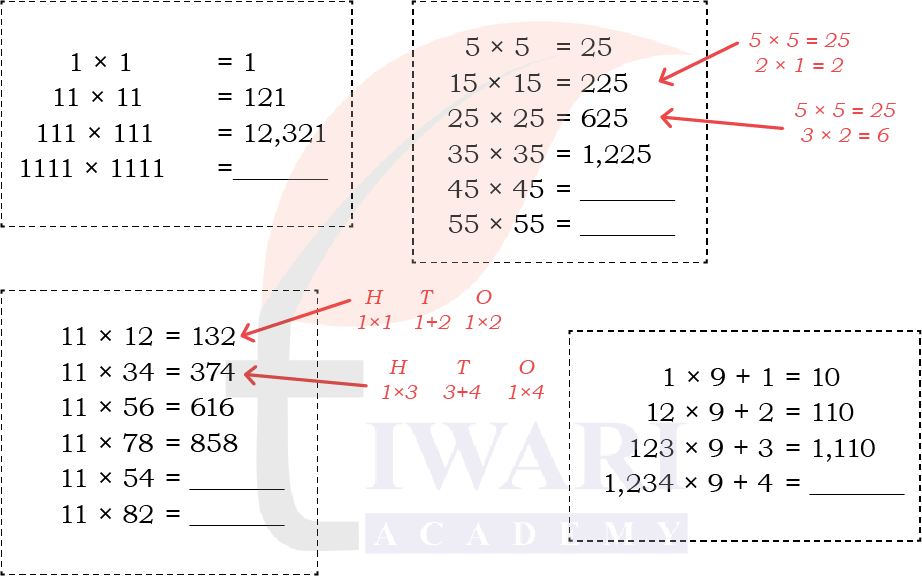
Answer:

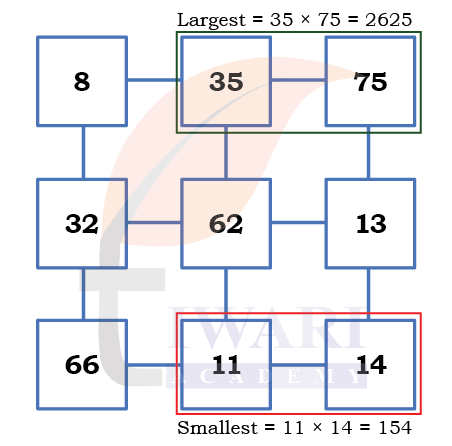
Here are some numbers. Remember number pairs from Grade 4? Any two adjacent numbers in a row or a column are number pairs. Can you identify the pair whose product is the smallest and another pair whose product is the largest? Do you need to find every product or can you find this by looking at the numbers?

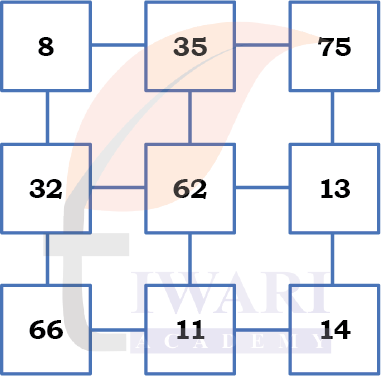
Answer: