NCERT Solutions for Class 6 Maths Chapter 14 Exercise 14.5 in Hindi and English medium updated for all State Boards. Browse the latest NCERT Class 6 Maths Chapter 14 Exercise 14.5 solutions on Practical Geometry at Tiwari Academy. Available in Hindi & English for CBSE and state boards.
6th Maths Exercise 14.5 Solutions in Hindi and English Medium
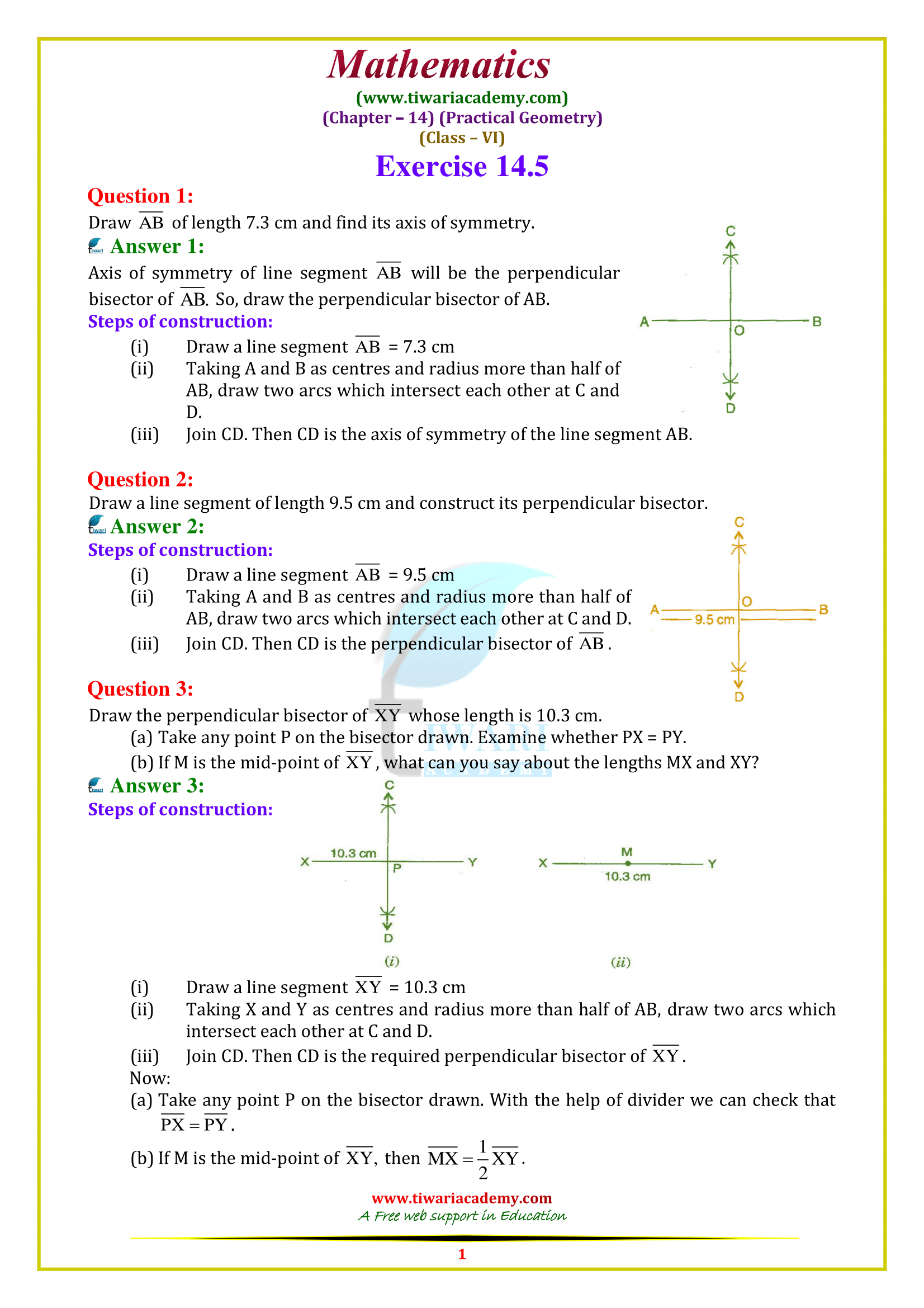
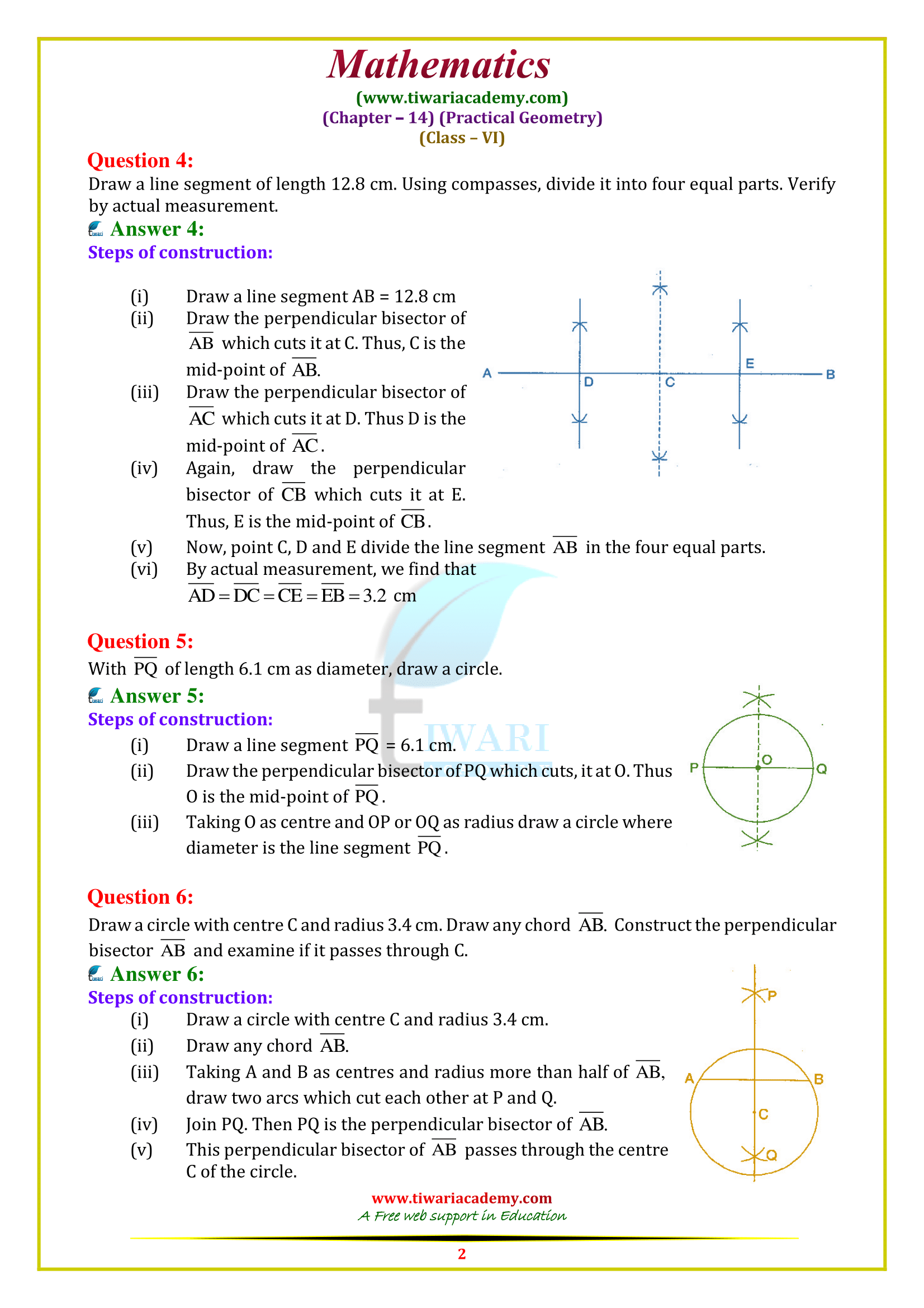
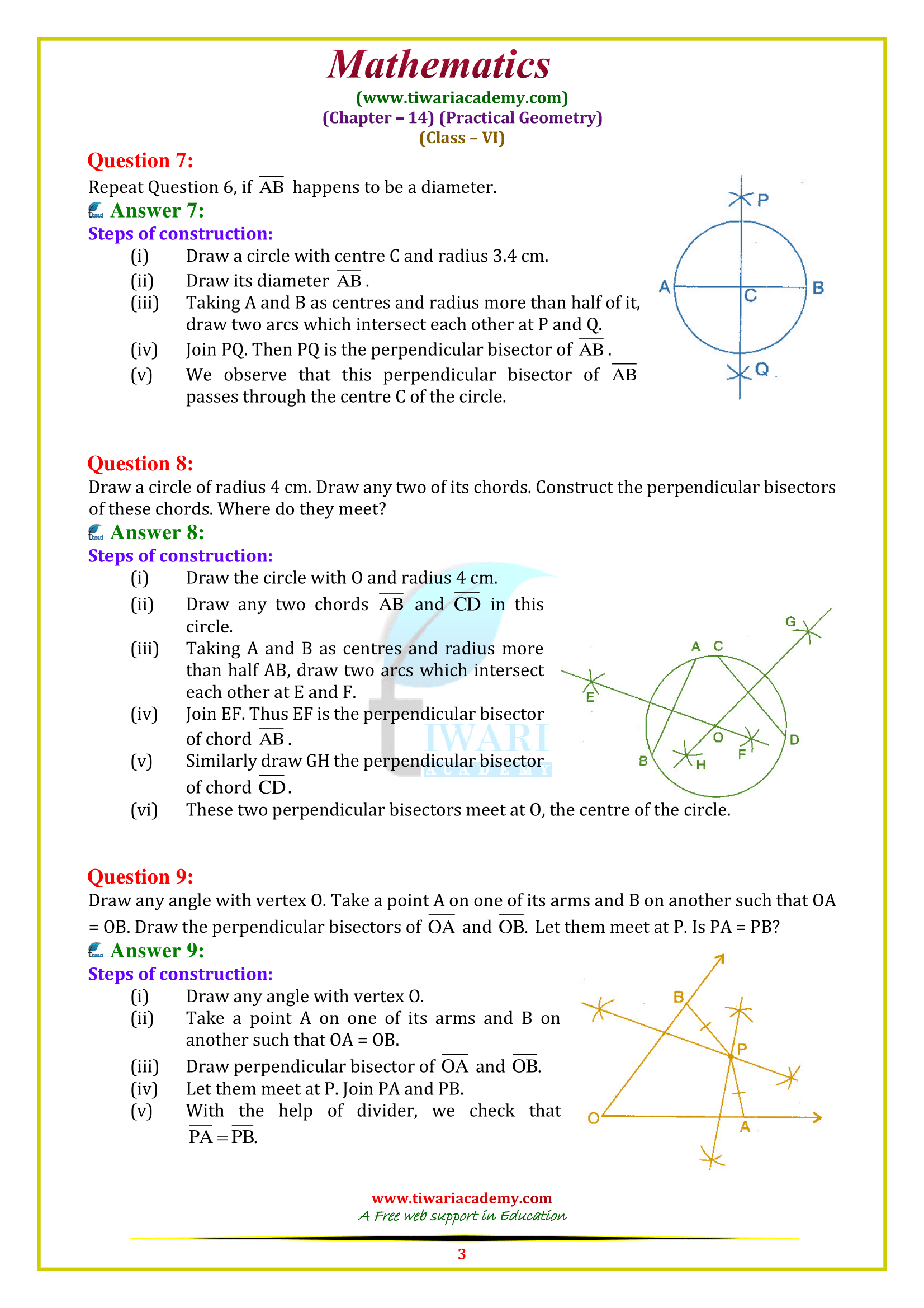
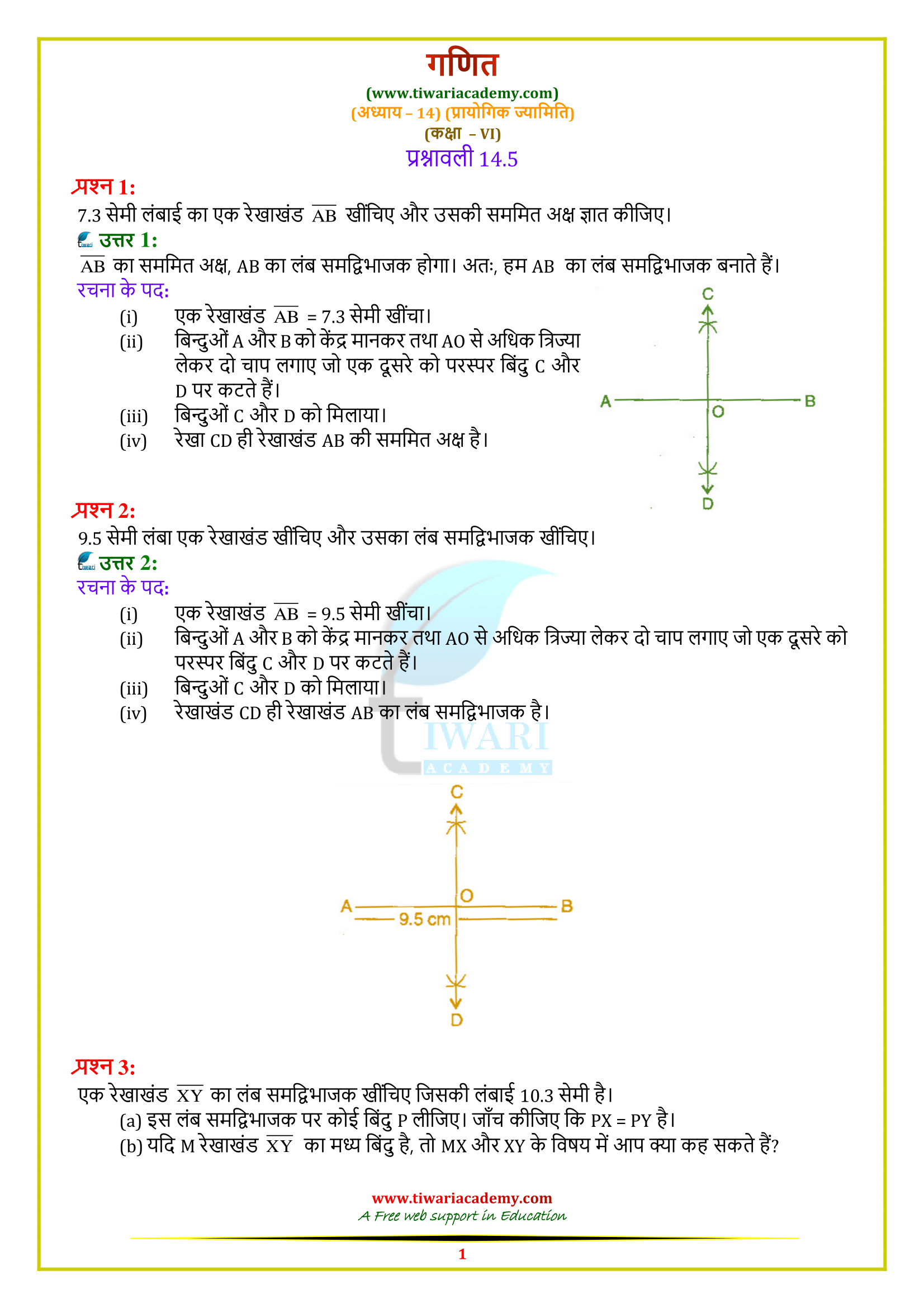
Class 6 Maths Chapter 14 Exercise 14.5 Solution
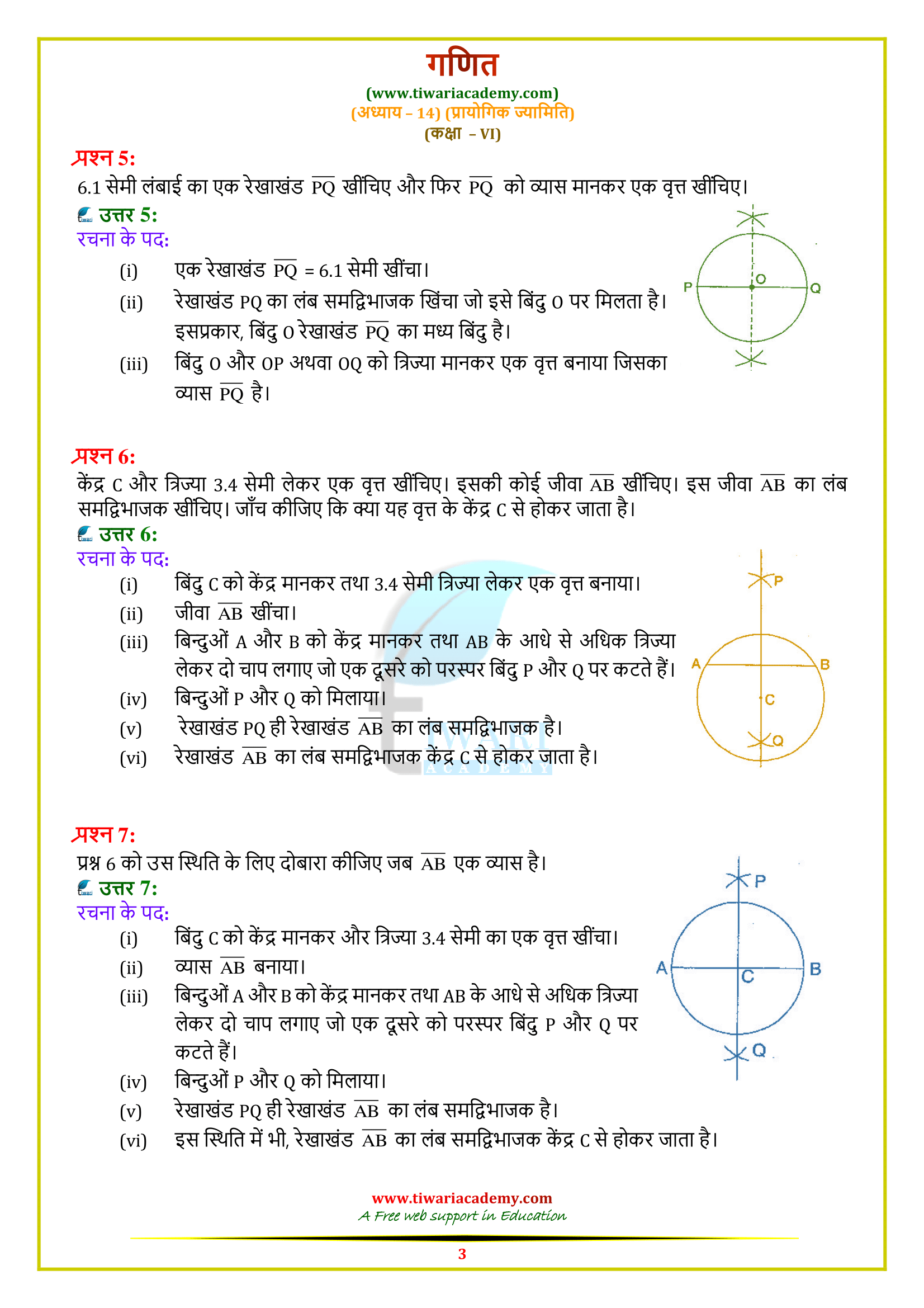
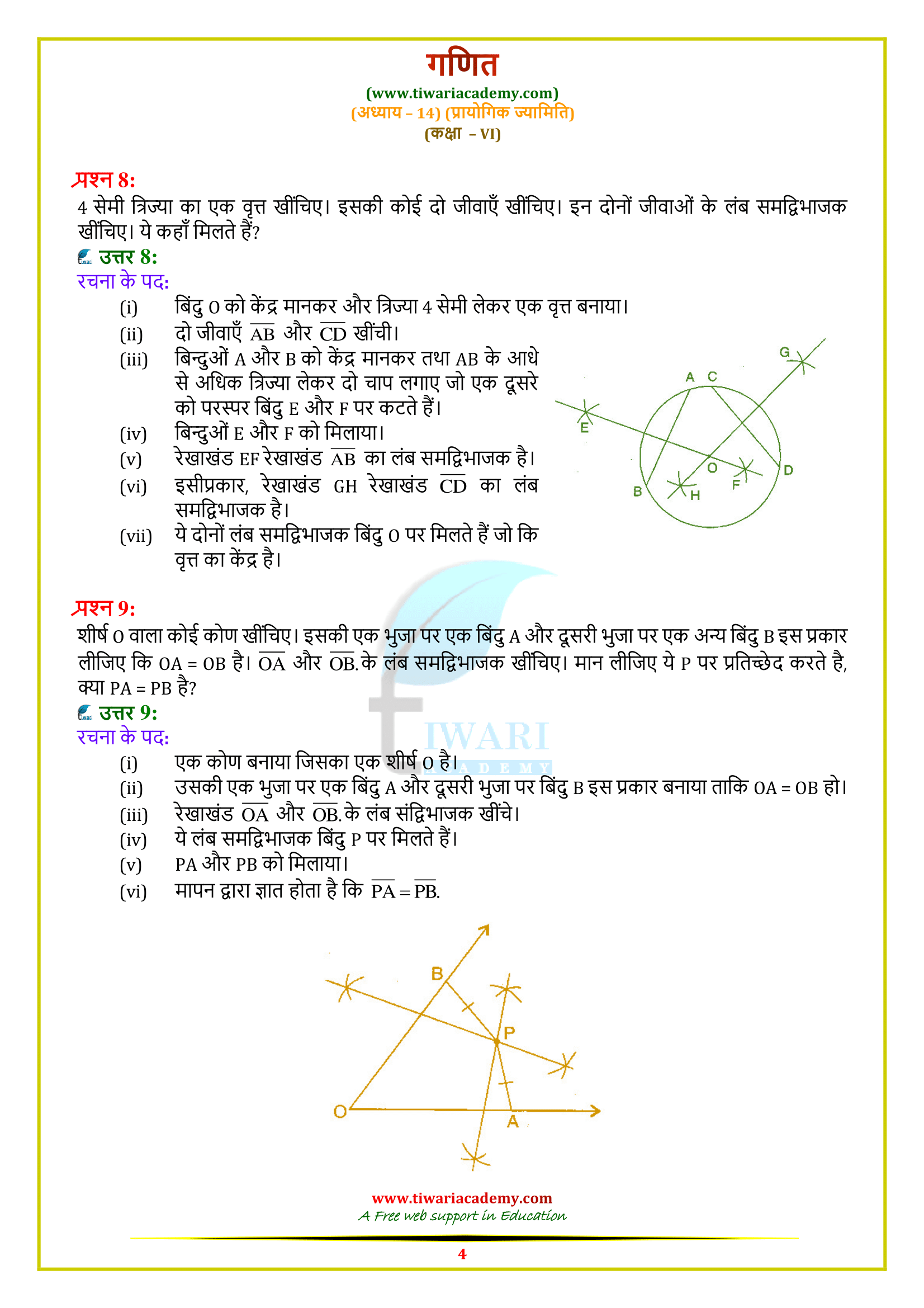
Class VI Maths Ex. 14.5 Practical Geometry based on textbook of NCERT (https://ncert.nic.in/) website in Hindi and English Medium free to use online or download in PDF file format. All the question answers are updated for CBSE academic session and State board students. Class 6 math NCERT exercise 14.5 explains how to draw a perpendicular bisector of a given line. Here we will learn to draw a line of symmetry also.
| Class: 6 | Mathematics |
| Chapter: 14 | Exercise: 14.5 |
| Topic Covered: | Practical Geometry |
| Content: | NCERT Textbook Solution |
| Medium: | English and Hindi |
Class 6 Maths Chapter 14 Exercise 14.5 Solution in Videos
To Construct an Angle Equal to a Given Angle
In order to construct an angle equal to a given angle ABC, we take the following steps:
Step-1: Draw an angle ABC.
Step-2: Draw a ray KJ.
Step-3: With B as centre draw an arc cutting BA and BC at P and Q respectively.
Step-4: With K as centre and the same radius as above, draw an arc cutting KJ at R.
Step-5: With R as centre and radius equal to PQ cut the previous arc at S.
Step-6: Join KS and draw ray KL. Angle LKJ so obtained is the required angle.
Verification: Measure angle ABC and angle LKJ with the help of a protractor. You will find that angle ABC = angle LKJ.
Class 6 Maths Exercise 14.5 Important Questions
What is the meaning of bisector of angle?
The (interior) bisector of an angle, also called the internal angle bisector, is the line or line segment that divides the angle into two equal parts. The angle bisectors meet at the in-center.
How many angle bisectors are possible in an angle?
An angle only has one bisector. Each point of an angle bisector is equidistant from the sides of the angle. The interior or internal bisector of an angle is the line, half-line, or line segment that divides an angle of less than 180° into two equal angles.
Can a ray be bisected?
A line of reflection must exist so that when the figure is folded along this line, each point on one side of the line maps to a corresponding point on the other side of the line. A ray cannot be bisected.
To Bisect a Given Angle
In order to bisect a given angle ABC, we take the following steps:
- Draw any angle ABC.
- With B as centre and a suitable radius draw an arc that cuts BA and BC at points M and N respectively.
- With M as centre and radius more than half of MN draw an arc.
- With the same radius and N as centre draw another arc to cut the first arc at R.
- Join BR and produce it to form ray BX. Then ray BX bisects angle ABC
- Verification: Measure angle CBX and angle XBA. You will find that angle CBX = angle XBA.
How many questions are there in exercise 14.5 of grade 6th Maths?
Exercise 14.5 of grade 6th Maths has nine questions. Questions 4, 7, and 8 of exercise 14.5 of class 6th Maths are most important compared to other questions of this exercise.
How many days are needed to complete exercise 14.5 of grade 6th Maths?
Students need a maximum of 2-3 days to complete exercise 14.5 of grade 6th Maths if they give 1 hour per day to this exercise. This time can increase or decrease because this time depends on the student’s working speed, efficiency, ability, and many other factors.
On which concepts exercise 14.5 of grade 6th Maths is based?
Exercise 14.5 of grade 6th Maths is based on the concept “Construction of the perpendicular bisector of a line segment”. This exercise is very logical and interesting.
Does exercise 14.5 of 6th class Maths have any examples?
No, exercise 14.5 of 6th class Maths doesn’t have any examples. This exercise has only 9 questions and no examples. Some questions of this exercise are simple and some questions are a little complex.