NCERT Solutions for Class 6 Maths Chapter 6 Exercise 6.2 in English and Hindi Medium updated for CBSE session 2024-25. The question answers and solutions of ex. 6.2 class 6th Maths are revised as per the latest NCERT books issued for CBSE 2024-25 examination.
6th Maths Exercise 6.2 Solution in Hindi and English Medium
Class 6 Maths Chapter 6 Exercise 6.2 Solution
Class VI Mathematics NCERT Ex. 6.2 of Integers updated for new academic session 2024-25 for CBSE Board and State board, who are using NCERT (https://ncert.nic.in/) Books, free to download. In Class 6 Maths Exercise 6.2, we will learn how to plot two or more different numbers (negative or positive) on number line. All the solutions are done using simple way and easy steps. Videos related to exercise 6.2 is also given with complete explanation.
| Class: 6 | Mathematics |
| Chapter: 6 | Exercise: 6.2 |
| Chapter Name: | Integers |
| Medium: | Hindi and English |
| Content Type: | Online Text and Videos |
Absolute Value of an Integer
The absolute value or numerical value of an integer is a whole number which is obtained by deleting the sign before it. Thus, the absolute value of +2 is 2; –3 is 3; + 7 is 7; – 8 is 8; 0 is 0.
On the number line shown by Fig., both points A and B are at a distance of 6 units from O. A is at a distance of 6 units from O (0) in the positive (right) direction. B is at a distance of 6 units from O (0) in the negative (left) direction. If we do not take note of the directions, we can say that both A and B are at a distance of 6 units from O. In other words, the absolute value of the distance of each from O is 6. The absolute value of an integer a is indicated by | a |. Thus, | +6 | means absolute value of +6; | –6 | means absolute value of –6. Since the absolute value of +6 and –6 is the same and each is equal to 6, we have | +6 | = | –6 | = 6. The absolute value of 0 is 0, i.e., | 0 | = 0.
The absolute value of an integer is always greater than 0 or equal to 0.
The absolute value of an integer is either greater or equal to the integer
Operations on Integers
Addition of Integers
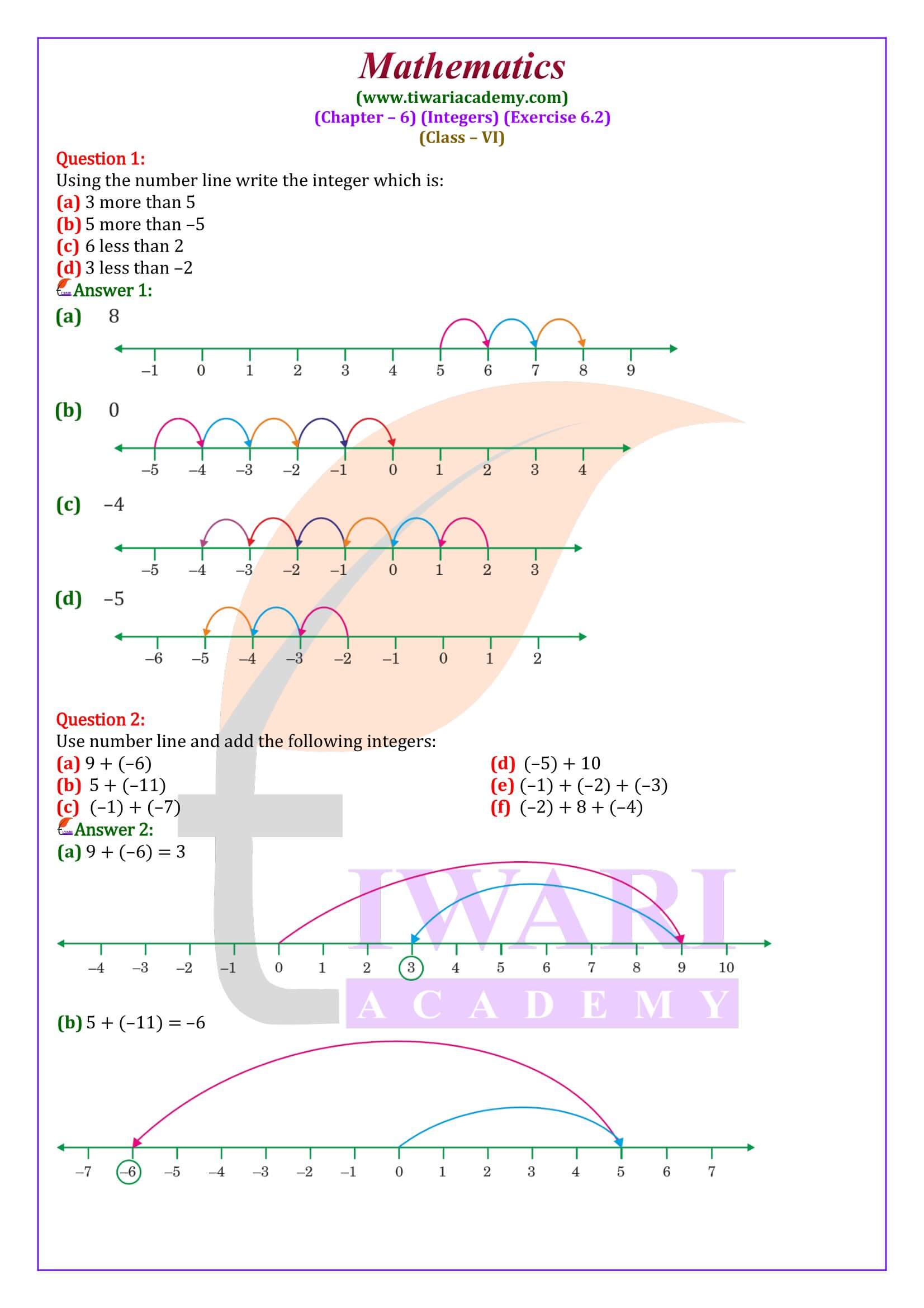
We know how to add two whole numbers using the number line. In this section, we shall extend this method to the addition of integers. Adding –4 to a number means moving 4 steps to the left of the number. Adding 4 to a number means moving 4 steps to the right of the number.
Rule 1:
If two positive integers or two negative integers are added, we add their values regardless of their signs and give the sum their common sign.
Class 6 Maths Exercise 6.2 Important Question with Answer
Write: (i) five negative integers just greater than –8, (ii) five negative integers just less than –12.
(i) Five negative integers just greater than –8, are -7, -6, -5, -4, -3
(ii) Five negative integers just less than –12, are -13, -14, -15, -16, -17
Find the absolute value of: (i) 5 (ii) 0 (iii) –7 (iv) – | –3 | (v) – | –8 | (vi) | 9 – 10 |
Absolute values of given numbers are:
(i) 5
(ii) 0
(iii) 7
(iv) – 3
(v) –8
(vi) 3
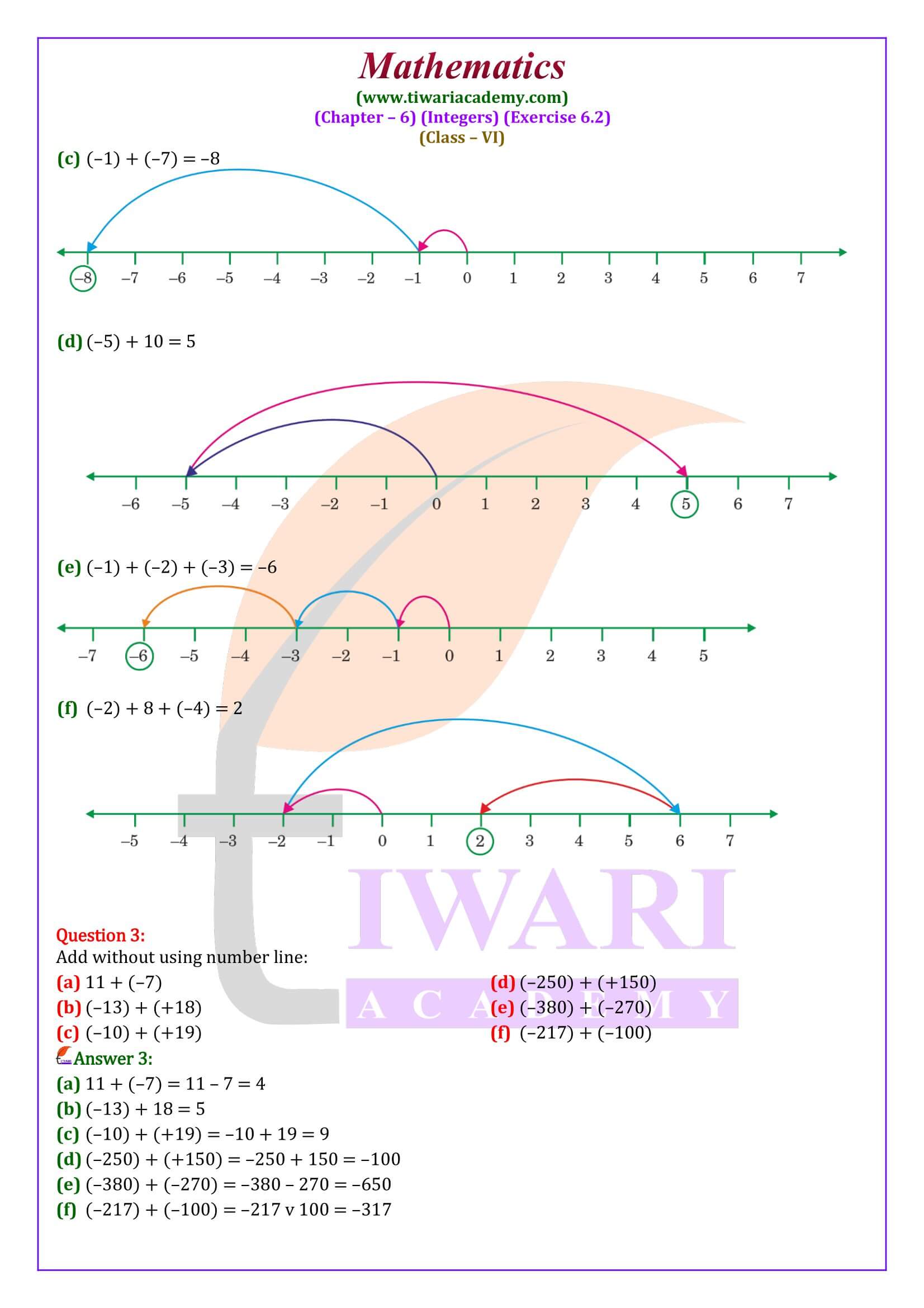
Add the following integers: (i) 121 and 249 (ii) –175 and –694 (iii) –212 and 427
(i) Both the integers are positive. So, by using the rule for addition of integers having the like signs, we have, 121 + 249 = 370
So, 121 + 249 = 370
(ii) Both the integers are negative. So, by using the rule for addition of integers having the like signs, we have, – 175 + – 694 – 869
So, (–175) + (–694) = –869.
(iii) Here, the integers to be added are of the unlike signs, therefore to add them, we find the difference of their absolute values and give the sign of the integer with more numerical value.
–212 + 427 = | 427 | – | –212 | = 427 – 212 = 215.
Rule 2:
To add a positive and a negative integer, we find the difference between their values regardless of their signs and give the sign of the integer with more numerical value.
Adding Two Positive Integers
Let us add +4 and +6
(+4) + (+6) = 10.
Class 6 Maths Exercise 6.2 Extra Questions for Practice
What do mean by absolute value of a number?
The absolute value or numerical value of an integer is a whole number which is obtained by deleting the sign before it. Thus, the absolute value of +2 is 2; –3 is 3; + 7 is 7; – 8 is 8; 0 is 0.
Find the successor of each of the following integers: (i) 0 (ii) –312 (iii) –89 (iv) –1 (v) –413 (vi) –815
Successor of the following integers:
(i) 1
(ii) –311
(iii) –88
(iv) 0
(v) –412
(vi) –814
Simplify: (i) (–850) + (–615) + 82 + (–225) (ii) 1250 + (–413) + 48 + (–609)
(i) (–850) + (–615) + 82 + (–225)
After simplifying we can write, – 850 – 615 + 82 – 225 = – 1690 + 82 = 1608
(ii) 1250 + (–413) + 48 + (–609)
After simplifying we can write, 1250 – 413 + 48 – 609 = 1298 – 1022 = 276
Adding Two Negative Integers
Let us add –2 and –5
(–2) + (–5) = –7.
Adding a Positive and a Negative Integer
Let us add +3 and –9
3 + (–9) = –6.
How many problems are there in exercise 6.2 of class 6 Maths?
Exercise 6.2 of class 6th Maths has four examples (Examples 3, 4, 5, 6) and five questions. The most important problems of this exercise that can come in the exams are example 6 and questions 2, 5.
How much time is needed to complete exercise 6.2 of grade 6th Maths?
Students need a maximum of 2 days to complete exercise 6.2 of class 6th Maths if they give 1 hour per day to this exercise. This time is not fixed, it is an approximate time.
Is exercise 6.2 of 6th Maths easy or tough?
Exercise 6.2 of class 6th Maths is not easy and not tough. It lies in the mid of easy and tough because some examples and questions of this exercise are easy, and some are complex. However, the difficulty level varies from child to child. So, exercise 6.2 of class 6th Maths is easy, or tough depends on children also. Some children find it difficult, some find it easy, and some find it in the middle of easy and difficult.
What will students learn in exercise 6.2 of class 6 Maths?
In exercise 6.2 of class 6th Maths, students will learn how to add integers using the number line and also how to add integers without using the number line. This exercise is interesting.