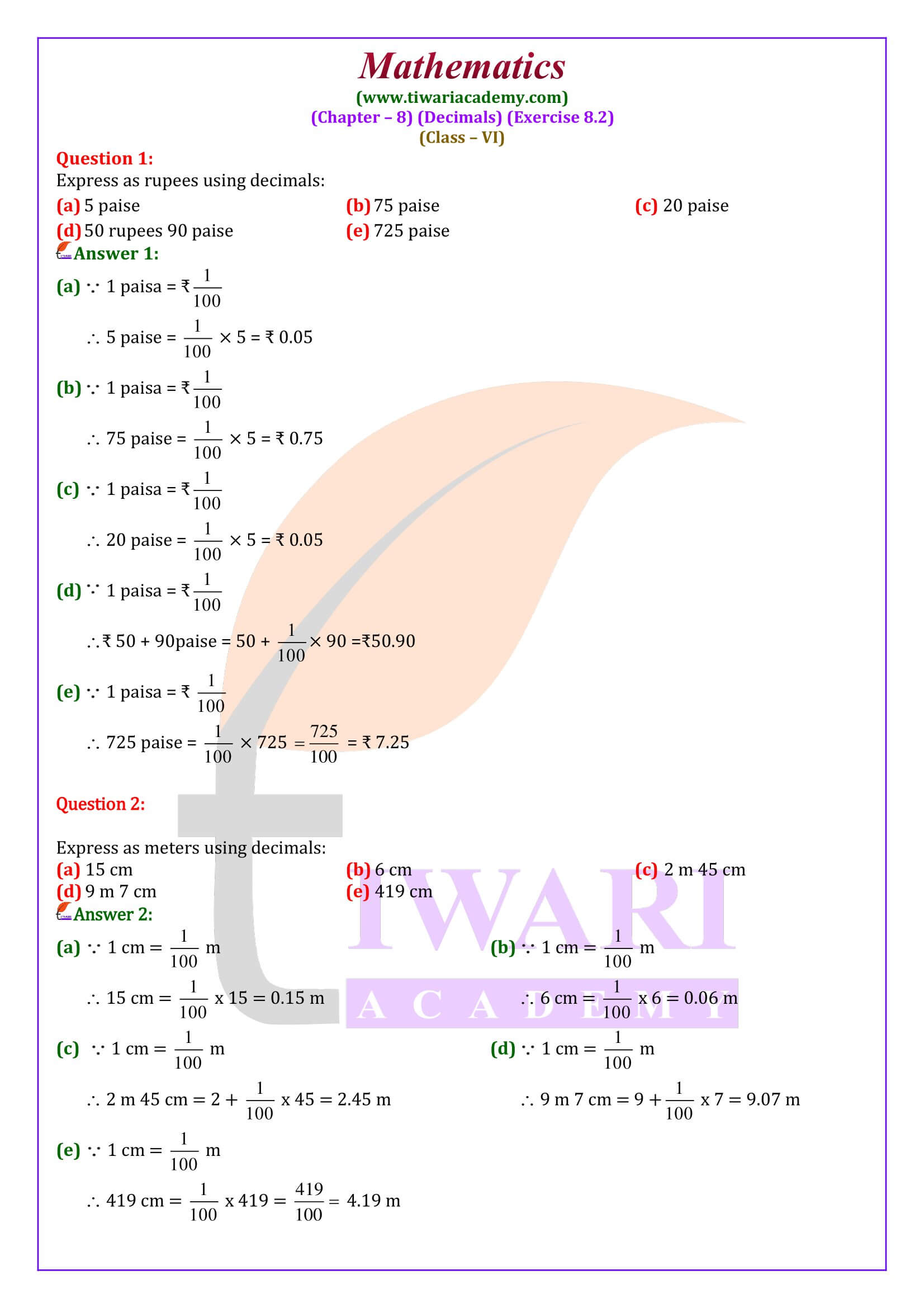
NCERT Solutions for Class 6 Maths Chapter 8 Exercise 8.2 in Hindi and English Medium updated for CBSE new session 2024-25. All the question answers explanation are revised according to rationalised syllabus and new NCERT Books for CBSE 2024-25 examination.
6th Maths Exercise 8.2 Solution in Hindi and English Medium
| Class: 6 | Mathematics |
| Chapter: 8 | Exercise: 8.2 |
| Topic Name: | Decimals |
| Content Type: | Explanation and Solutions |
| Session: | CBSE 2024-25 |
| Medium: | Hindi and English Medium |
Class 6 Maths Chapter 8 Exercise 8.2 Solution
Class VI Mathematics Ex. 8.2 of chapter 8 Decimals free to download in PDF updated in Hindi and English Medium for CBSE 2024-25 exams. Step by step solutions are given in explanation video. Do all the questions yourself first and see the NCERT (https://ncert.nic.in/) solutions if any doubt. NCERT Class 6 Maths Book exercise 8.2 all questions solutions are given in PDF and Videos format, so that student face no difficulty during the study.
Conversion of a Decimal Fraction into common Fraction
To convert a decimal fraction into a common fraction, we remove the decimal point from the given decimal and the number thus obtained becomes the numerator of the common fraction. The denominator is formed by putting 1 and the number of zeroes at the right of 1 equal to the number of digits at the right of the decimal point in the given decimal fraction.
Class 6 Maths Exercise 8.2 Extra Question with Answer
Convert the following decimals into fractions in the lowest terms: (i) 6.4 (ii) 12.05 (iii) 7.504
(i) 6.4 = 64/10 = 32/5 = 6(2/5)
(ii) 12.05 = 1205/100 = 241/20 = 12(1/20)
(iii) 7.504 = 7504/1000 = 938/125 = 7(63/125)
Convert 2(3/16) into decimal.
2(3/16) = (2 x 16 + 3)/16 = 35/16
Now, 35/16 = (35 x 625)/ 16 x 625 = 21875/10000 = 2.1875
Hence, 2(3/16) = 2.1875
To understand the above rule, study the following example:
Example- 1:
Convert the following decimals into fractions in the lowest terms:
(i) 0.4 (ii) 0.28 (iii) 0.305
(i) 0.4 = 04/10 = 4/10 = 2/5
(ii) 0.28 = 028/100 = 7/25
(iii) 0.305 = 0305/1000 = 61/200
Class 6 Maths Exercise 8.2 Important Questions
How many decimal places do banks use?
As for banking – my understanding is that they keep like 5 decimal places, and round at the last possible time. There are actually laws pertaining to how these figures are rounded, specifically when doing foreign currency exchanges.
How do we convert decimals into fractions?
To convert a decimal to a fraction, place the decimal number over its place value. For example, in 0.6, the six is in the tenths place, so we place 6 over 10 to create the equivalent fraction, 6/10. If needed, simplify the fraction.
What is 1.75 converted to a fraction?
Take 1.75 = 1 75/100. Next, simplify the fraction part to the lowest common term. e.g. 75/100 = 3/4.
Converting a Fraction into a Decimal
To convert a fraction into a decimal, first we change the given common fraction into an equivalent fraction whose denominator is 10 or 100 or 1000 etc. After that we change it into decimal.
Example 3:
Convert the following fractions into decimals: (i) ½ (ii) 3/5 (iii) 2(1/25)
- (i) ½ = (1 x 5)/ (2 x 5) = 5/10 = 0.5
- (ii) 3/5 = (3 x 2)/ (5 x 2) =6/10 = 0.6
- (iii) 2(1/25) = 51/25 = (51 x 4)/ (25 x 4) = 204/100 = 2.04
How many questions are there in exercise 8.2 of class 6 Maths NCERT Book?
Exercise 8.2 of class 6th Maths has 5 questions. In questions 1, 2, 3, and 5, each question has five parts, and students have to express these 5 parts in rupees, metres, cm, and kg respectively using decimals. In question 4, four parts are given and students have to express these 4 parts in km using decimals.
Is exercise 8.2 of class 6th Maths simple to solve?
Exercise 8.2 of class 6th Maths is not at all challenging. This exercise is overall a simple exercise. In this exercise, students have to remember conversions formulas only to solve this exercise. Once students learn conversion formulas on tips then students find this exercise very easy. However, the difficulty level of any exercise depends on students also. Some students find exercise 8.2 easy, and some students find exercise 8.2 difficult.
Which questions of exercise 8.2 of class 6th Maths have a chance to come in the final exam?
Exercise 8.2 of class 6th Maths is important from the exam point of view. Every year questions come from exercise 8.2 of class 6th Maths in the exams. There are 5 questions and no example in exercise 8.2. All the questions of this exercise are significant and can come in the exams. But the most important questions of this exercise that have more chance to come in the final exam are question 1 (d), question 2 (c), (d), question 3 (d), question 4, question 5 (d), (e).
How much time, students need to do exercise 8.2 of class 6th Maths?
Exercise 8.2 of class 6th Maths is a very short exercise. It has only 5 questions and no example. Students need a maximum of 2 days to complete exercise 8.2 of class 6th Maths if they give 1-2 hours per day to this exercise. This time is an approximate time. This time can vary because no students can have the same working speed, efficiency, ability, etc.