Class 7 English Grammar Chapter 17 Direct and Indirect Speech. If we give the exact words used by the speaker. This is called Direct Speech. If we do not give the exact words of the speaker but give only the substance of what he said. This is called Indirect Speech. For example, Ram said, “Hari is a poor boy.” is direct speech whereas Ram said that Hari was a poor boy is Indirect Speech.
Class 7 English Grammar Chapter 17 Direct and Indirect Speech with Examples
Mastering the art of narration in English involves a deep understanding of Direct and Indirect Speech, as beautifully captured in Chapter 17 of Class 7 English Grammar. When we opt to convey the exact, unaltered words of a speaker, we utilize Direct Speech. A quintessential example of this is: “Ram said, ‘Amit is a poor boy.’” Here, we’re recounting Ram’s statement verbatim, retaining the original essence and tone.
| Class: 7 | English Grammar |
| Chapter: 17 | Direct and Indirect Speech |
| Books: | Textbook and Revision Book |
| Academic Session: | 2025-26 |
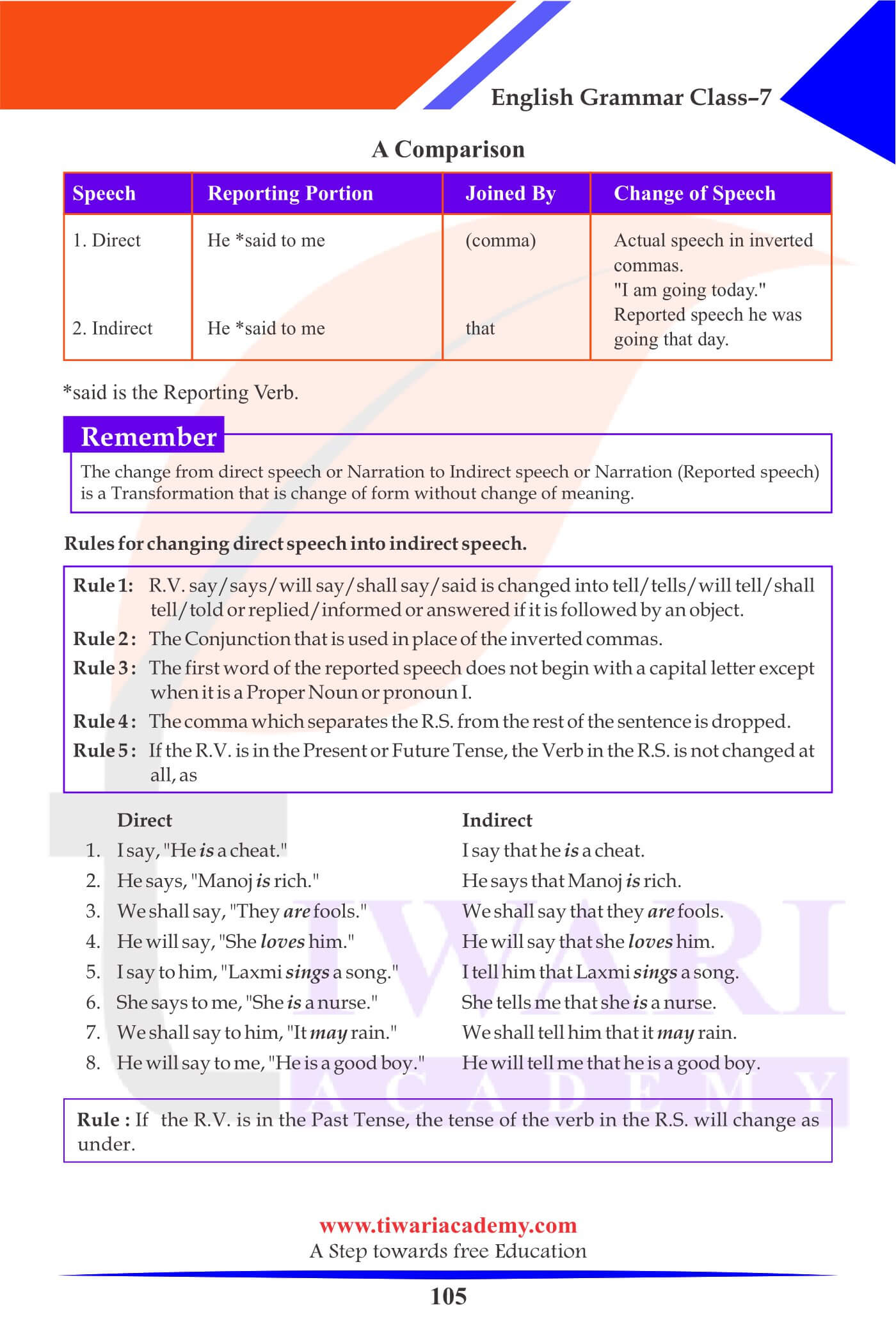
Direct Speech
- The exact words of the speaker are put within inverted commas. (” “).
- The first word of the R.S. begins with a capital letter.
- A comma is placed after the Reporting Verb to separate it from the second part of the sentence.
On the other hand, Indirect Speech offers a subtle shift, focusing on the essence rather than the exact phrasing of the speaker’s words. Instead of quoting Ram directly, we might say, “Ram mentioned that Amit was a poor boy.” This approach, while retaining the core message, omits the direct quotation. By distinguishing between these two styles, students can enhance their linguistic skills, ensuring effective and accurate communication in various contexts.
Indirect Speech
- The reported words are not placed within inverted commas.
- No comma is placed after “said”.
- The reported speech is introduced by the conjunction that/if/to/what/when, etc.
- The tense of the verb in the R.S. is changed from the Present to the Past.
Rules for changing direct speech into indirect speech
- R.V. say/says/will say/shall say/said is changed into tell/tells/will tell/shall tell/told or replied/informed or answered if it is followed by an object.
- The Conjunction that is used in place of the inverted commas.
- The first word of the reported speech does not begin with a capital letter except when it is a Proper Noun or pronoun I.
- The comma which separates the R.S. from the rest of the sentence is dropped.
- If the R.V. is in the Present or Future Tense, the Verb in the R.S. is not changed at all.
| Direct | Indirect |
|---|---|
| He will say, “She loves him.” | He will say that she loves him. |
| I say, “He is a cheat.” | I say that he is a cheat. |
| I say to him, “Laxmi sings a song.” | I tell him that Laxmi sings a song. |
| She says to me, “She is a nurse.” | She tells me that she is a nurs. |
| We shall say, “They are fools.” | We shall say that they are fools. |
| He says, “Manoj is rich.” | He says that Manoj is rich. |
Exception to Rule
If the Reported Speech expresses some universal truth, factual truth, habitual fact, natural fact, historical fact, scientific fact, the tense of the verb in R.S. is not changed into the Past.
| Direct | Indirect |
|---|---|
| Naresh said, “Two and two make four.” | Naresh said that two and two make four. |
| Father said to me, “The air has weight.” | Father told me that the air has weight. |
| Mother said to me, “Union is strength.” | Mother told me that union is strength. |
| He said, “Sea water testes saltish.” | He said that sea water tastes saltish. |
| Neeraj said, “God loves all things below.” | Neeraj said that God loves all things below. |
| The teacher said, “The earth is round.” | The teacher said that the earth is round. |
More to Know
- The Reporting Verb said or told are changed into asked/inquired/demanded etc.
- If the sentence begins with the helping verb or Modal Auxiliary then “if” or “whether” is used as conjunction.
- If a Positive Question in the R.S. has the helping verb do/does,do or does is dropped.
- The interrogative form changes into the Assertive form.
- The same word is used to introduce the R.S. if the Question begins with an Interrogative Pronoun or Adverb, such as what, which, whom and when, where, how and why etc.