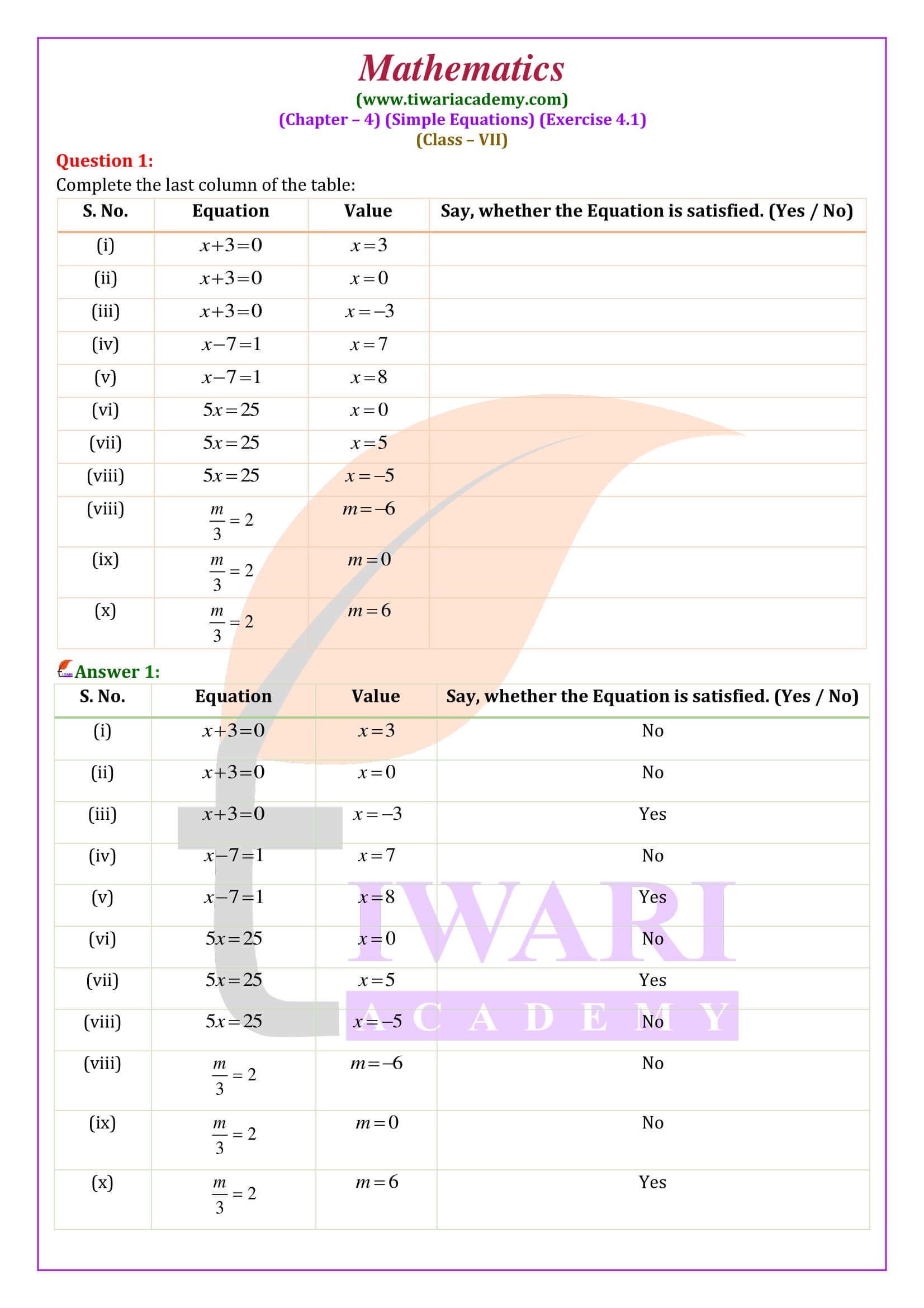
NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.1 Simple Equations Hindi and English Medium updated for academic session 2024-25. The solutions of ex. 4.1 class VII mathematics are revised according to new syllabus and current textbooks issued for CBSE 2024-25 examination.
NCERT Class 7 Maths Exercise 4.1 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 4 | Exercise: 4.1 |
| Topic Name: | Simple Equations |
| Content: | Text, Images and Videos |
| Session: | CBSE 2024-25 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 4 Exercise 4.1 Solution
All the solutions are question answers are based on latest NCERT Books issued for 2024-25. In class 7 math exercise 4.1 we will learn to format simple linear equations in one variable. Exercise 4.1 also provides the way to solve the simple linear equations in one variable.
Class 7 Maths Chapter 4 Exercise 4.1 Solution in Videos
Linear Equation
Linear equations are those equations that are of the first order. These equations are defined for lines in the coordinate system.
For example:
(i) 5 less than twice a number x can be written as 2x – 5.
(ii) One sixth of a number x can be written as.
(iii) Three times of the sum of x and 7 can be written as 3 x (x + 7).
Class 7 Maths Exercise 4.1 Important Questions
How does linear equations relate to real life?
Almost any situation where there is an unknown quantity can be represented by a linear equation, like figuring out income over time, calculating mileage rates, or predicting profit. Many people use linear equations every day, even if they do the calculations in their head without drawing a line graph.
What are the three methods used to solve linear equations?
There are three ways to solve systems of linear equations: substitution, elimination, and graphing. Let’s review the steps for each method.
What are the applications of linear equations?
Applications of Linear Equations:
Solve word problems involving relationships between numbers. Solve geometry problems involving perimeter. Solve percent and money problems including simple interest. Set up and solve uniform motion problems.
Solve: 5x – 6 = 4x – 2.
We have:
5x – 6 = 4x – 2
Or, 5x – 4x = – 2 + 6 [transposing 4x to LHS and -6 to RHS]
Or, x = 4.
Thus, x = 4 is a solution of the given equation.
Now consider the following statements
(i) 6 more than a number x is 13 can be written as x + 6 = 13.
(ii) times a number n is 15 can be written as = 15.
(iii) A number y divided by 7 gives 5 can be written as = 5.
In each of the above statements the symbol ‘=’ (is equal to) appears. A statement involving symbol ‘=’ is called a statement of equality.
Equation
A statement of equality which involves one or more variables is called an equation. The expression to the left side of the equality sign (=) is called the left hand side (L.H.S.) and that of right side to the equality sign is called right hand side (R.H.S.) of the equation.
Linear Equation
An equation in which the highest power of the variables is one, is called a linear equation.
Example: Equations 2x + 4 = 6, (y/3) + 1 = 2 and 2z + 5/2 = 37/2 are linear equations.
Solution of an Equation
The value of unknown variable which statistics equality of both sides of the equation is known as the solution or root of the equation.
Let us verify that x = 3 is the solution (root) of the equation 4x + 6 = 18.
L.H.S. = 4x + 6 For x = 3 L.H.S. = 4 x 3 + 6 = 12 + 6 = 18 = R.H.S.
Hence, x = 3 is the solution of the equation 4x + 6 = 18.
Rules of solving an equation
(i) The same quantity can be added to both sides of an equation without changing the equality.
(ii) The same quantity can be subtracted from both sides of an equation without changing the equality. (iii) Both sides of an equation may be multiplied by the same nonzero number without changing the equality.
(iv) Both sides of an equation may be divided by the same nonzero number without changing the equality.
Are there any examples in exercise 4.1 of class 7th Maths? Give an overview.
Yes, there are four examples (examples 1, 2, 3, 4) in exercise 4.1 of class 7th Maths. All the examples of this exercise are nice. In example 1, students have to write the given statements in the form of equations, in example 2, students have to convert the given equations in the statement form. Example 3 and example 4 are the word problems.
Which questions of exercise 4.1 of class 7th Maths can students expect in the unit tests?
Exercise 4.1 of class 7th Maths has 6 questions and 4 examples (Examples 1, 2, 3, 4). All questions and examples of exercise 4.1 of 7th standard Maths are important at their places. But, the most important questions and examples of this exercise that students can expect in the unit tests are questions 2, 4 (i), 5 (i), 6 (i), and examples 2, 3, 4.
Is exercise 4.1 of grade 7th Maths complicated to solve and understand?
Exercise 4.1 of grade 7th Maths is not very simple and not very complicated. It lies in between simple and complicated. Students find some questions and illustrations of this exercise hard and some questions and illustrations easy. Sometimes most students face problems in understanding the language of questions. However, the difficulty level of any exercise depends on students also. According to some students exercise 4.1 is easy, some students find exercise 4.1 in between easy and hard, and some find it complicated.
Is exercise 4.1 of class 7th Maths lengthy?
Exercise 4.1 of class 7th Maths is not very lengthy. This exercise has 6 questions and four examples (examples 1, 2, 3, 4). Students need a maximum of 3-4 days to complete exercise 4.1 of class 7th Maths if they honestly and seriously give 1-2 hours per day to this exercise. This time may increase or decrease because this time depends on student’s working speed, ability, efficiency, and many other factors.