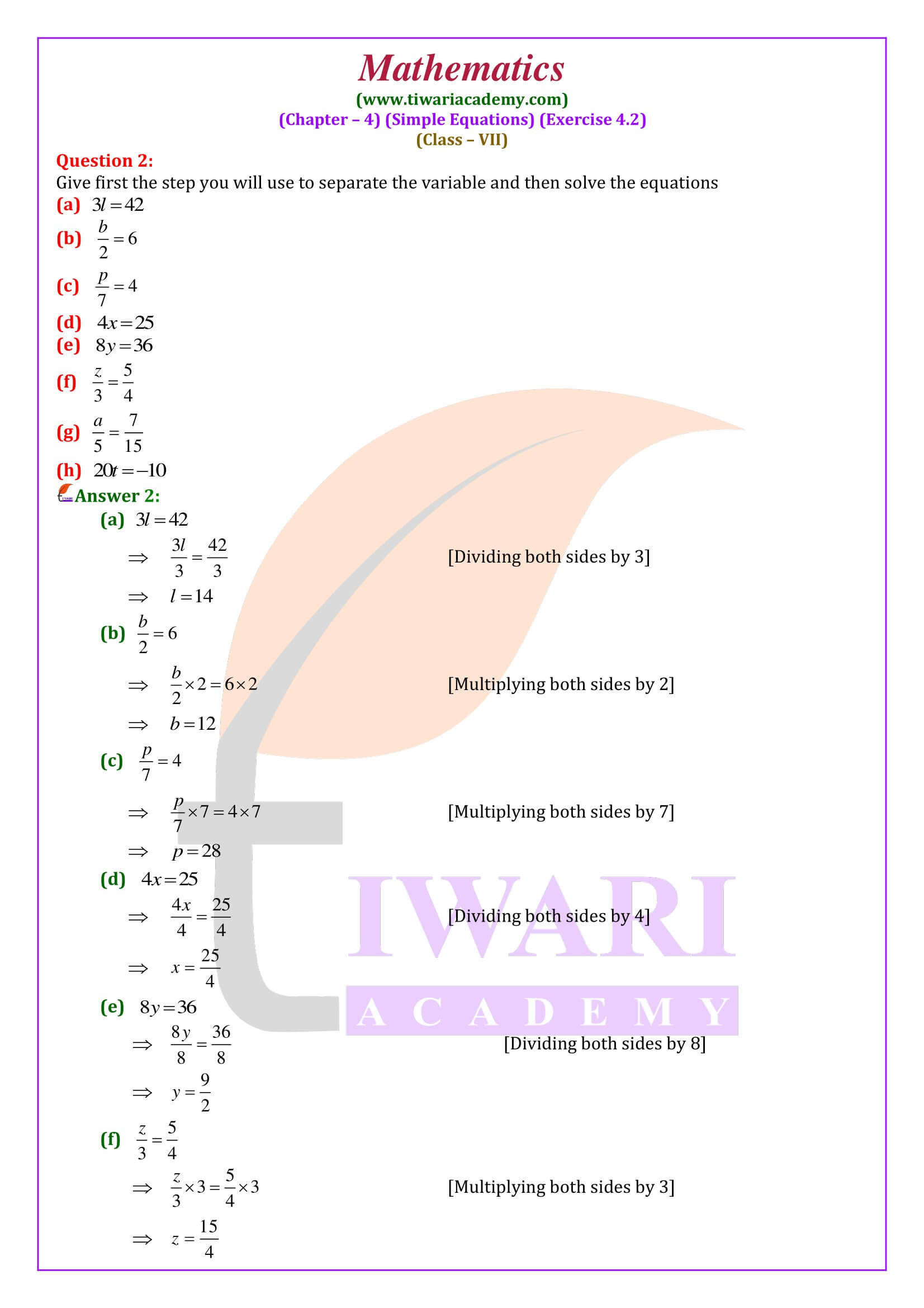
NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.2 Simple Equations in Hindi and English Medium prepared for new CBSE session. Students of class 7 can take the benefits of revised solutions of questions given in ex. 4.2 mathematics based on new textbooks for academic year 2024-25.
NCERT Class 7 Maths Exercise 4.2 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 4 | Exercise: 4.2 |
| Chapter Name: | Simple Equations |
| Content Type: | PDF, Images and Videos |
| Session: | Academic Year 2024-25 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 4 Exercise 4.2 Solution
Solution are based on latest CBSE books for class 7 issued for session 2024-25. Step by step solutions of exercise 4.2 of class 7 are given here in simplified format, so that student can understand easily. Videos Solution are also given with the PDF solution.
Class 7 Maths Chapter 4 Exercise 4.2 Solution in Videos
Class 7 Maths Exercise 4.2 Extra Questions
Solve: 2y + 11/4 = (1/3) y + 2
We have:
2y + 11/4 = (1/3) y + 2
Or, 2y – (1/3) y = 2 – 11/4
Or, (6y – y)/3 = (8 – 11)/4
Or, 5y/3 = -3/4
Or, y = – 9/20
Thus, y = – 9/20 is a solution of the given equation.
Substituting y = -9/20 in the given equation. we get,
LHS = 2 x (-9/20) + 11/4 = -9/10 + 11/4 = (-18 + 55)/20 = 37/20
RHS = 1/3 x (-9/20) + 2 = -3/20 + 2/1 = (-3 + 40)/20 = 37/20
So, LHS = RHS
Hence, y = -9/20 is a solution of the given equation.
Solve: (5x – 4)/8 – (x – 3)/ 5 = (x + 6)/4.
We have:
(5x – 4)/8 – (x – 3)/ 5 = (x + 6)/4
Multiplying both sides by 40, the LCM of 8, 5 and 4, we get
5 (5x – 4) – 8 (x – 3) = 10(x + 6)
Or, 25x – 20 – 8x + 24 = 10x + 60
Or, 17x + 4 = 10x + 60 [transposing 10x to LHS and 4 to RHS]
Or, 17x – 10x = 60 – 4
Or, 7x = 56
Or, x = 56/7 = 8
Thus, x = 8 is a solution of the given equation.
Check: Substituting x = 8 in the given equation, we get,
LHS = (5 x 8 – 4)/8 – (8 – 3)/ 5 = 36/8 – 1 = 28/8 = 7/2
RHS = (8 + 6)/4 = 14/4 = 7/2
So, LHS = RHS
Hence, x = 8 is a solution of the given equation.
Linear Equation in One Variable
The linear equations in one variable is an equation which is expressed in the form of ax + b = 0, where a and b are two integers, and x is a variable and has only one solution.
For example, 2x + 3 = 8 is a linear equation having a single variable in it.
Class 7 Maths Exercise 4.2 Important Questions
Why do we use linear equations?
Linear equations are an important tool in science and many everyday applications. They allow scientist to describe relationships between two variables in the physical world, make predictions, calculate rates, and make conversions, among other things. Graphing linear equations helps make trends visible.
How do you know if a system is linear?
If the relationship between y and x is linear (straight line) and crossing through origin then the system is linear. If you find any time t at which the system is not linear then the system is non-linear.
Solve: 0.3x + 0.4 = 0.28x + 1.16
We have:
0.3 x + 0.4 = 0.28x + 1.16
Or, 0.3 x – 0.28x = 1.16 – 0.4 [by transposition]
Or, 0.02x = 0.76
x = 0.72/0.02 = 72/2 = 38.
So, x = 38 is a solution of the given equation.
Simple Equations
As we have seen, while solving equations one commonly used operation is adding or
subtracting the same number on both sides of the equation.
Transposition
Any term of an equation may be taken from one side to the other with a change in its sign. This does not affect the equality of the statement. This process is called transposition.
Transposing a number (i.e., changing the side of the number) is the same as adding or subtracting the number from both sides. In doing so, the sign of the number has to be changed.
Which questions of exercise 4.2 of class 7th Maths are compulsory to do?
Exercise 4.2 of 7th standard Maths has 4 questions and one example (example 5). All problems of this exercise are significant. All problems of exercise 4.2 are compulsory to do. Students can’t skip any problem of exercise 4.2 for the exams.
Is exercise 4.2 of 7th standard Maths lengthy or short?
Exercise 4.2 of 7th Standard Maths is not lengthy. It has 4 questions and one example (example 5). Children require at most 2 days to complete exercise 4.2 of 7th Standard Maths if they give 1-2 hours per day to this exercise. This time also depends on children’s ability, efficiency, working speed, and many other factors.
Is Exercise 4.2 of 7th Standard Maths easy to solve and understand?
Exercise 4.2 of class 7th Maths is not easy and not tough to solve and understand. It lies in the mid of simple and hard because some problems of this exercise are simple, and some are complicated. However, the difficulty level of any exercise varies from student to student. So, exercise 4.2 of class 7th Maths is easy or hard depends on the students also. Some students find it hard, some find it simple, and some find it in the middle of simple and difficult.
Which sums of exercise 4.2 of grade 7th Maths are of the same type?
Exercise 4.2 of grade 7th Maths has 4 questions and one example (example 5). Questions 1, 2, 3 are of the same kind. Example 5 and question 4 are of the same type.