NCERT Solutions for Class 8 Maths Chapter 13 Exercise 13.2
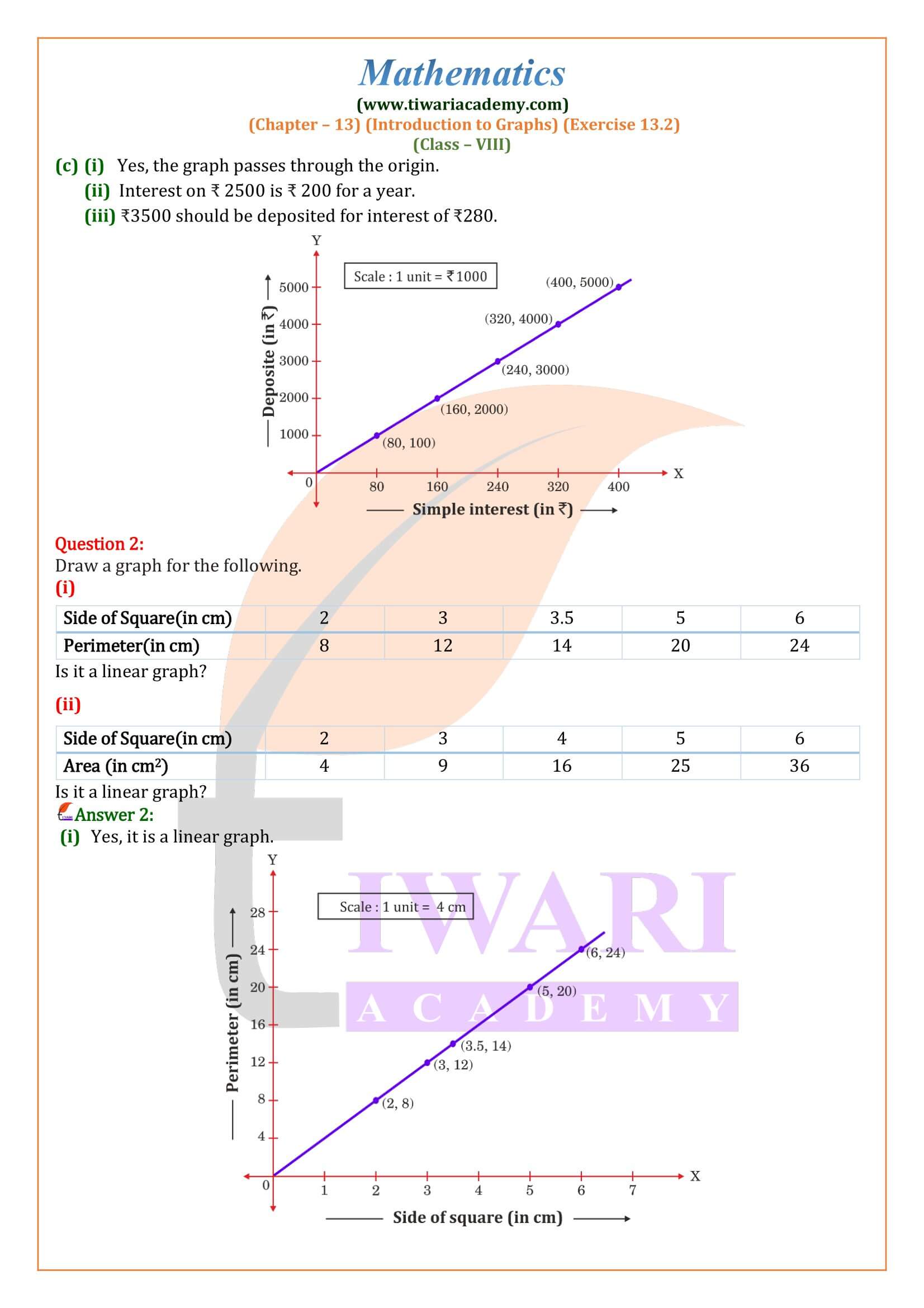
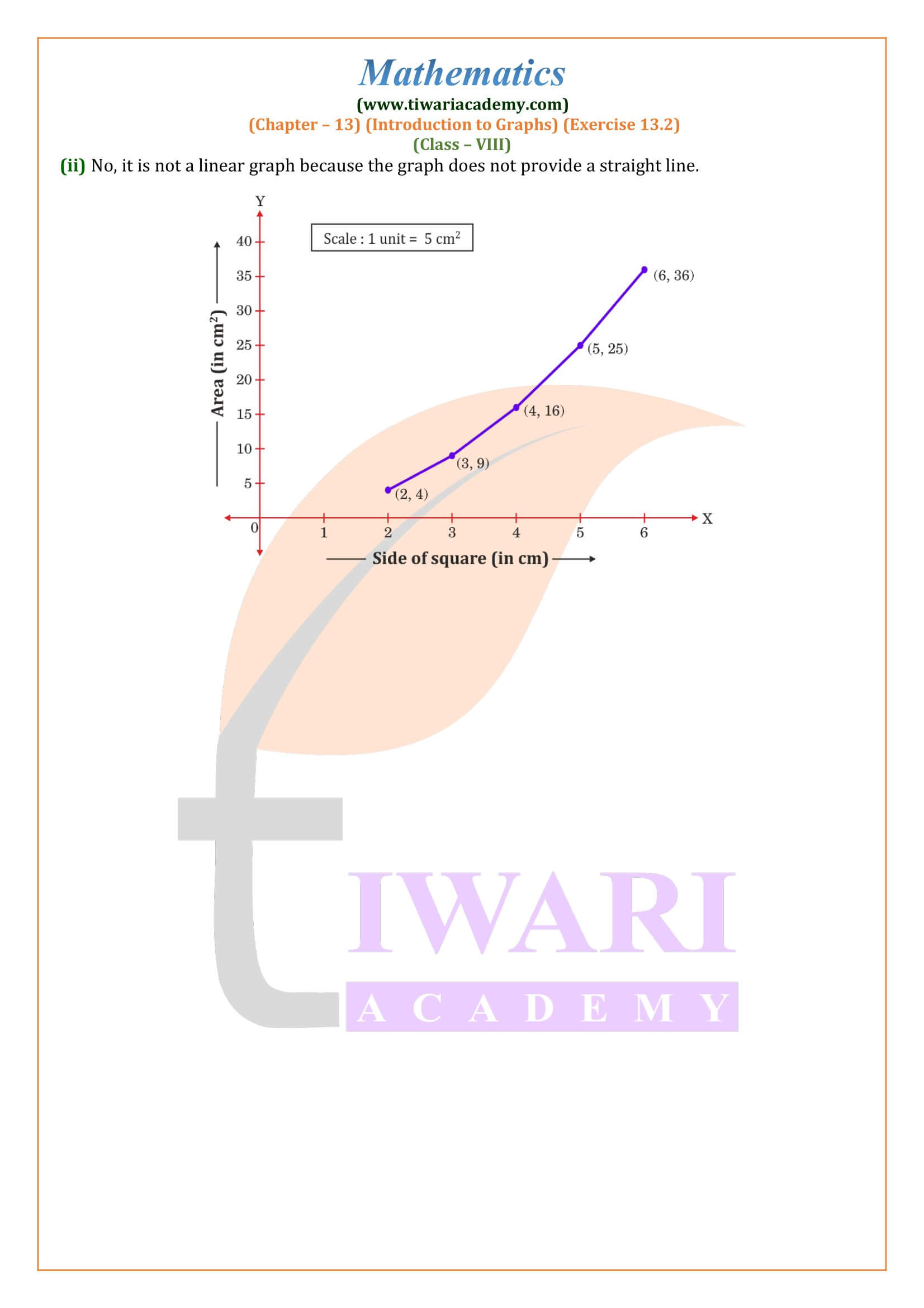
NCERT Solutions for Class 8 Maths Chapter 13 Exercise 13.2 (Ex. 13.2) Direct and Inverse Proportions in PDF file format free to download without any login or registration. All the contents are updated for session 2021-22 for CBSE and state board students.
In class 8 mathematics exercise 13.2 questions are based on inverse proportion and its application in daily life. All the questions are solved with easy method so that students can understand easily.
Class 8 Maths Chapter 13 Exercise 13.2 Solution
| Class: 8 | Mathematics |
| Chapter: 13 | Direct and Inverse Proportions |
| Exercise: 13.2 | Hindi and English Medium Solutions |
CBSE NCERT Class 8 Maths Chapter 13 Exercise 13.2 Solution in Hindi and English Medium
Free App for Class 8 Solutions
Class 8 Maths Chapter 13 Exercise 13.2 Solution in Videos
Inverse Proportion (Inverse Variation)
We know that with more speed, a car will take less time to cover a fixed distance. Similarly, more workers will finish a work in less time.
Thus, there are cases wherein two variables are related to each other in such a way that on increasing the one, the other decreases proportionally and vice versa.
Inverse proportion
Two quantities x and y are said to be in inverse proportion if xy = k, where k is a constant.
Thus, x1 y1 = x2 y2 = x3 y3 = ……….. = k.
If 45 men can do a piece of work in 49 days. In how many days’ will 35 men do it?
Let the required number of days be x. Then, we have:
Clearly, less men will take more days to finish the work.
So, it is a case of inverse proportion.
So, 45 x 49 = 35 X x
Or, x = (45 x 49)/35 = 63
Hence, required number of days = 63
A can do a piece of work in 30 days while B can do the same work in 24 days. In how many days can they complete it, if they work together.
A’s 1 day’s work = 1/30
B’s 1 day’s work = 1/24
(A + B)’s 1 day’s work = 1/30 + 1/24 = 3/40
3/40 work A and B can do in 1 day
A and B can do the work in 40/3 days = 13(1/3) days
Hence, A and B together can do work in 13(1/3) days.
What is a real life example of inverse variation?
(i) For example, when you travel to a particular location, as your speed increases, the time it takes to arrive at that location decreases. When you decrease your speed, the time it takes to arrive at that location increases. So, the quantities are inversely proportional.
(ii) If family has less members, more saving (provided that the family has the same amount of income). More members, less saving (income is still the same). It is an inverse variation. More members is in joint variation to earning and saving.
How do you solve inverse variation problems?
(i) Identify the input, x, and the output, y.
(ii) Determine the constant of variation. …
(iii) Use the constant of variation to write an equation for the relationship.
(iv) Substitute known values into the equation to find the unknown.
What have you learned about inverse variation?
The main idea in inverse variation is that as one variable increases the other variable decreases. That means that if x is increasing y is decreasing, and if x is decreasing y is increasing. The number k is a constant so it’s always the same number throughout the inverse variation problem.
