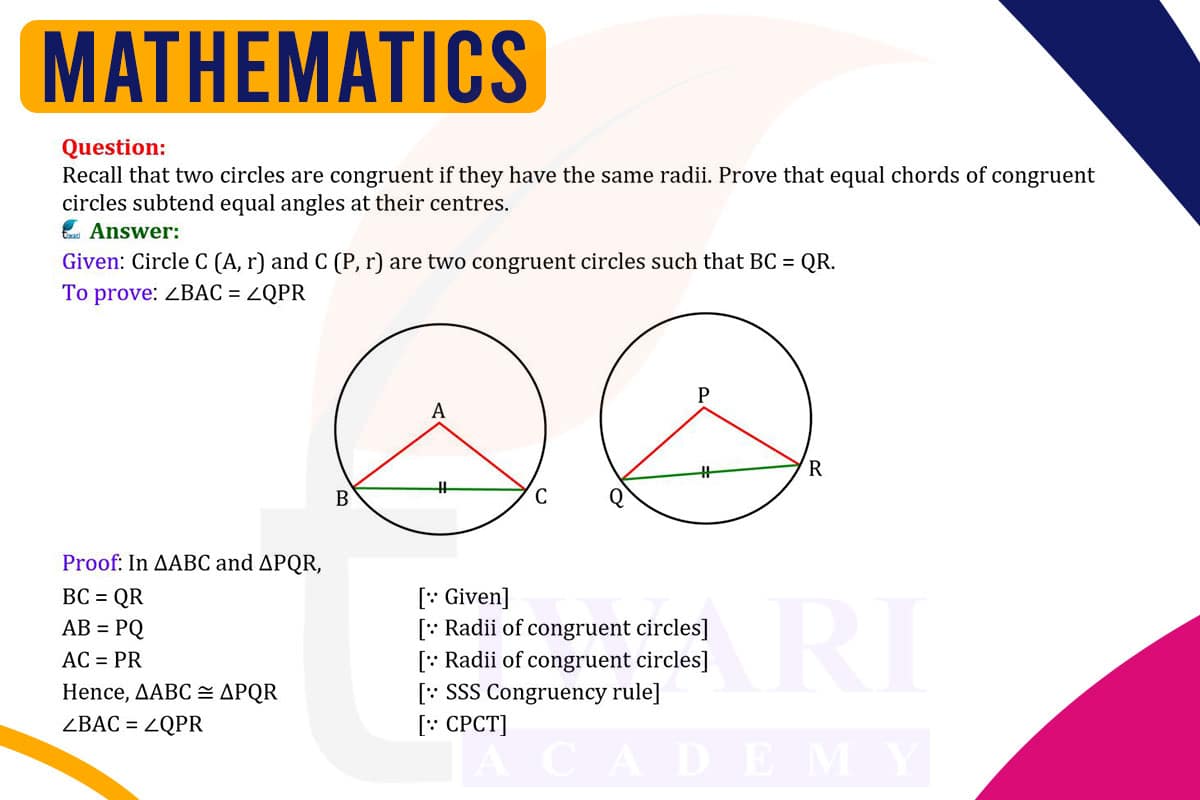
To prove that equal chords of congruent circles subtend equal angles at their centres, consider two congruent circles with equal chords. Since the circles are congruent, they have the same radius. For each circle, draw the radius to the endpoints of the chord. This forms two isosceles triangles in each circle. Since the chords are equal and the radii of the circles are equal (being congruent circles), the isosceles triangles are congruent by the Side-Side-Side (SSS) postulate. Therefore, the angles subtended by the equal chords at the centres of the congruent circles are equal, as they correspond to angles in congruent triangles.
Let’s discuss in detail
Congruent Circles and Chords
Congruent circles are circles of the same radius, and they play a crucial role in understanding geometric relationships. When we discuss chords within these circles, a chord is a straight line segment whose endpoints lie on the circle. A fundamental property of interest is the relationship between chords and the angles they subtend at the center of their respective circles. This relationship becomes particularly intriguing when we consider equal chords in congruent circles, leading to insightful conclusions about the angles these chords subtend.
Understanding Equal Chords
Equal chords are chords of the same length. In the context of congruent circles, these chords maintain their equality across both circles. The significance of equal chords lies in their geometric properties, especially how they relate to the angles they subtend at the center of a circle. The length of a chord in a circle is directly related to the size of the angle it subtends at the center. This relationship forms the basis of our exploration into proving that equal chords of congruent circles subtend equal angles at their centers.
The Role of Isosceles Triangles
In each congruent circle, drawing radii to the endpoints of an equal chord forms an isosceles triangle. This is because the two radii are equal in length, and the chord acts as the base. The properties of isosceles triangles are essential here: not only do they have two equal sides (the radii), but the angles opposite these sides are also equal. These angles are the ones subtended by the chord at the center of the circle.
Congruence of Triangles in Congruent Circles
Since the circles are congruent and the chords are equal, the isosceles triangles formed in each circle are also congruent. This congruence is established by the Side-Side-Side (SSS) postulate, which states that if three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent. The equal sides here are the two radii and the chord. This congruence of triangles is a pivotal step in proving our main proposition.
Equal Angles Subtended by Equal Chords
The congruence of the isosceles triangles leads to the conclusion that the angles subtended by the equal chords at the centers of the congruent circles are equal. This is because congruent triangles have corresponding angles that are equal. Therefore, the angle subtended by one chord in its circle is equal to the angle subtended by the congruent chord in the other circle. This equality of angles is a direct result of the congruence of the isosceles triangles formed by the chords and the radii.
Geometric Harmony in Congruent Circles
In conclusion, the geometric harmony of congruent circles and equal chords reveals a beautiful symmetry in geometry. The proof that equal chords of congruent circles subtend equal angles at their centers not only demonstrates a fundamental geometric principle but also highlights the elegance and interconnectedness of geometric shapes and their properties. This understanding is crucial in the broader study of geometry and its applications in various fields, from architecture to astronomy.
Discuss this question in detail or visit to Class 9 Maths Chapter 9 for all questions.
Questions of 9th Maths Exercise 9.1 in Detail

