NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.2 of Continuity and Differentiability in Hindi and English Medium updated for new session 2025-26. All the questions of ex. 5.2 of class 12 Maths are updated as per rationalised syllabus for CBSE 2025-26.
12th Maths Exercise 5.2 Solutions in Hindi and English Medium
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.2
Grade XII Mathematics ex. 5.2 solution and all the digital contents with Videos solutions are free to use and download. NCERT Sols for class 12 Maths are updated for academic session 2025-26. UP Board and MP Board students also using the same NCERT Books as the CBSE Students, these NCERT Solutions are also useful for UP Board and MP Board students. Download UP Board Solutions and MP Board Solutions for Class 12 Maths in Hindi Medium free of cost. Video solutions in Hindi and English Medium are also available along with PDF solutions. We have updated all the NCERT textbook Solutions on the basis of the requirements and suggestions received by the students and parents. All the contents on Tiwari Academy is free to use. If someone is facing problem to access the content, please contact us for help. We will help you as soon as possible.
| Class: 12 | Mathematics |
| Chapter 5: | Exercise 5.2 |
| Topic Name: | Continuity and Differentiability |
| Content: | NCERT Exercise Solutions |
| Session: | CBSE 2025-26 |
| Medium: | English and Hindi Medium |
12th Maths Exercise 5.2 Solutions
NCERT CBSE Solutions for Class 12 Maths Chapter 5 Exercise 5.2 Continuity and Differentiability English as well as Hindi Medium online free to use as well as download for new academic session 2025-26. In this exercise, you will learn more about the uses of PRODUCT RULE, QUOTIENT RULE and CHAIN RULE in derivatives. It is just the continuation of Class 11th Limits and Derivatives. Give your view related to questions asked by users for NIOS or CBSE board.
About Continuity and Differentiability Exercise 5.2
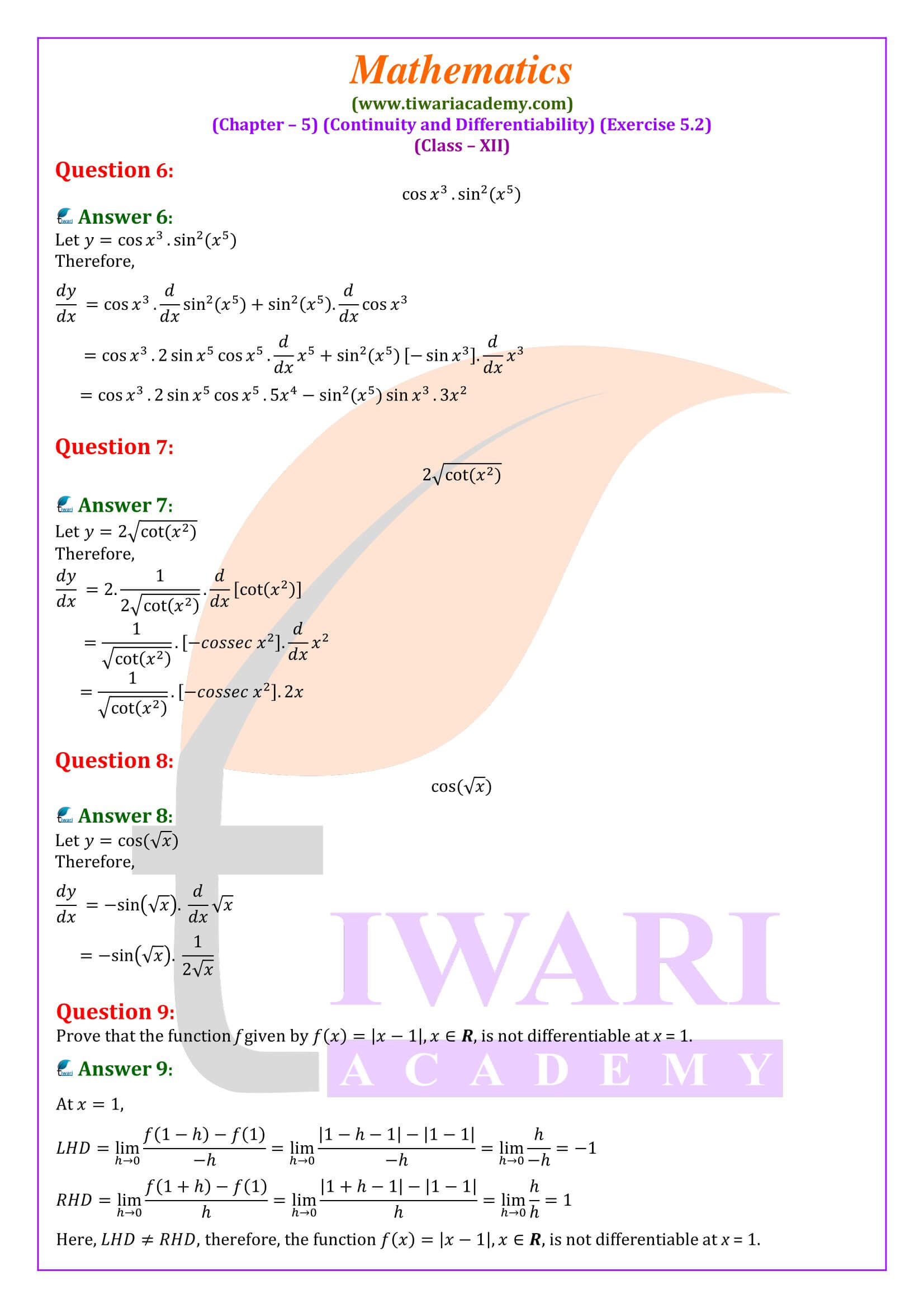
In Exercise 5.2 Questions 1 to 8 are based on differentiation by Product Rule, Quotient Rule and Chain Rule. Few of them are tricky but most of them are easy. Only question number 6 is little bit difficult in solving. During the solutions of this question, please keep in mind that sin²x and (sin x)² are the same functions. Question number 9 and 10 are based on differentiability, in which we have to find Left Hand Derivative LHD and Right Hand Derivatives RHD to verify whether the function is differentiable on a real point or not. The method of solving a modulus function may differ by teacher to teacher. Finally this exercise provides a good practice to revise derivatives of functions.
Feedback and Suggestions
NCERT Solutions are updated according to latest NCERT Books 2025-26 following the new CBSE Syllabus for new session. If you are facing any difficulty, please notify us through discussion forum, so that we can rectify. You can ask your doubts regarding to NIOS board also.
What is the core motive of exercise 5.2 of 12th standard Maths?
The core motive of exercise 5.2 of 12th standard Maths is to teach the following things to the students:
- Differentiability
a. If a function f is differentiable at a point c, then it is also continuous at that point.
b. Every differentiable function is continuous. - Derivatives of composite functions.
a. Chain rule.
Is exercise 5.2 of grade 12th Maths important from the first term exam point of view?
Yes, from the exam point of view, exercise 5.2 of grade 12th math is important. Questions can come from this exercise in the board exams. All questions and examples of this exercise are important. But the most important examples and questions of this exercise are examples 21, 22, 23, and questions 4, 5, 6, 7, 8, 9, 10.
What are the easiest questions of exercise 5.2 of grade 12th Maths Book?
Questions 1, 2, 3 and examples 21, 22 are the easiest questions of exercise 5.2 (class 12 Maths) compared to other questions of this exercise. Also, these questions are the favourite questions of students because these questions are straightforward, and students do these questions without facing any challenge.
How much time do students need to complete exercise 5.2 class 12th mathematics?
Students need a maximum of 2 days to complete exercise 5.2 (chapter 5) of class 12th mathematics if they give 1 hour per day to this exercise. This time also depends on student’s speed, efficiency and capability.
Which problems of exercise 5.2 of class 12th Maths are complex?
Example 23 and questions 4, 5, 6, 7, 8, 9, 10 are complex problems of exercise 5.2 of class 12th Maths. These problems are complicated because most of the students face difficulty while solving these problems. Students should solve these questions with full concentration.