NCERT Solutions for Class 5 Maths Mela Chapter 7 Shapes and Patterns

Page 93

Let Us Try

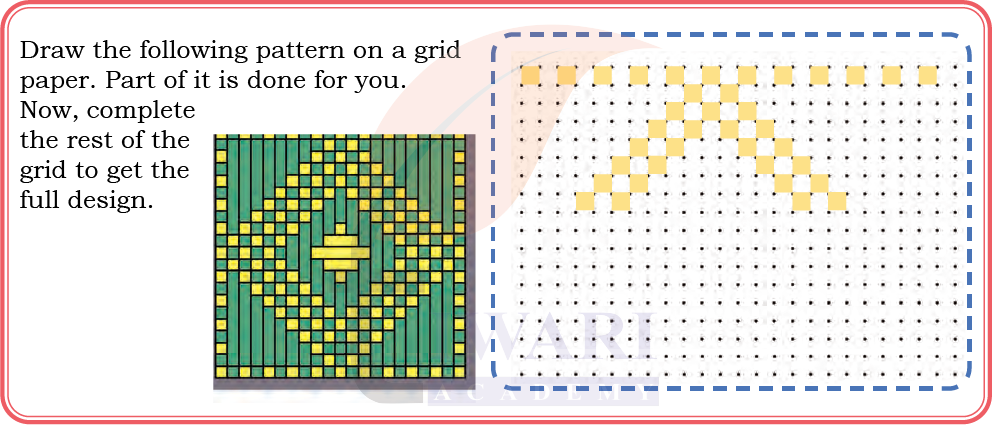
Answer:

Page 94

Find Out

Can regular triangles fit together at a point without any gap? How many of them fit together? (A sample triangle is given at the end of the book). Do you see that regular triangles fit around a point as shown here?

Answer:
Yes, regular triangles can fit together. 6 triangles can fit around a single point. The corners of all 6 triangles will meet perfectly without any gaps.

Can squares (a regular 4-sided shape) fit together around a point without any gap or overlap? Try it out using cutouts of squares (a sample square is given at the end of the book). How many squares did you need?
See AnswerYes, squares can fit around a point without leaving any gap or overlap.
The total angle around a point is 360° and the corner angle of a square is 90°.
360° ÷ 90° = 4.
So, exactly four squares fit around a point.

Can five squares fit together around a point without any gaps or overlaps? Why or why not?
See AnswerNo, five squares cannot fit together . If you try to fit 5 squares around a point, they will either overlap or leave a gap. The corners of a square are 90 degrees. 5 squares would need 5 x 90 = 450 degrees of space, but a full circle is only 360 degrees.

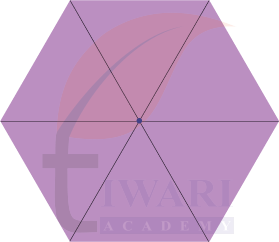
Can regular hexagons (6-sided shapes with equal sides) fit together around a point without any gaps or overlaps? Try and see (a sample hexagon is given at the end of the book). How many fit together at a point?
See AnswerYes, regular hexagons can fit together around a point without any gaps or overlaps.
The angle at each corner of a regular hexagon is 120° and the total angle around a point is 360°.
360° ÷ 120° = 3.
So, 3 hexagons fit together perfectly around a point.

Page 95

Here is a tessellating pattern with more than one shape.
What shapes have been used in this pattern?

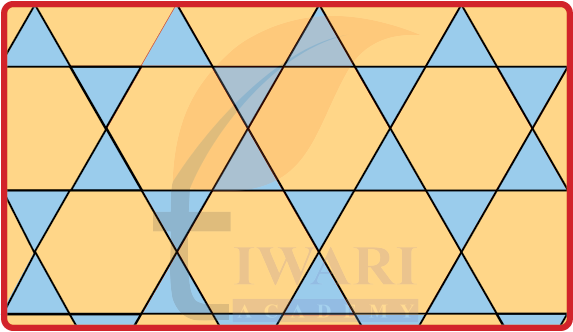
See AnswerEquilateral triangles and regular hexagons.

Continue the pattern given below and colour it appropriately.

Answer:

Do regular octagons fit together without any gaps or overlaps? Try drawing the same and check.

See AnswerNo regular octagons do not fit together without any gaps. If we try to put octagons together, we will see gaps between them or overlaps.

Page 96

Look at the pattern given below. What shapes are coming together at the marked points? Are the same set of shapes coming together at these points?
Continue the pattern and colour it appropriately.

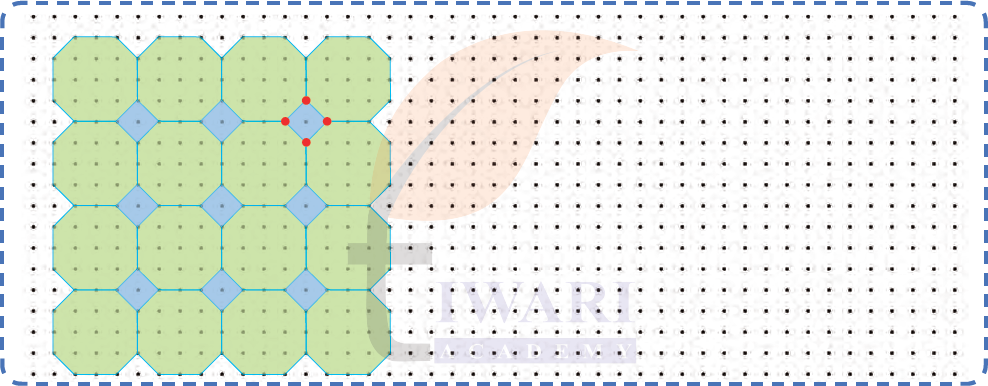
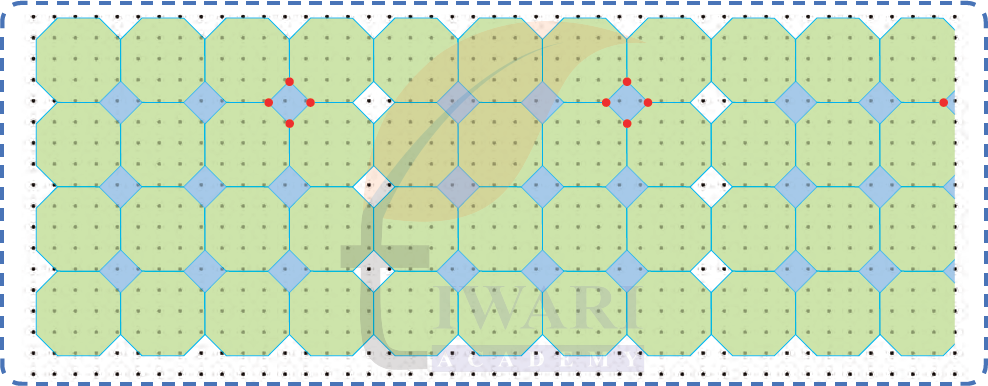
See AnswerAt each marked point, two octagons and one square come together.
Yes, the same set of shapes (two octagons and one square) meet at all the red-marked points.

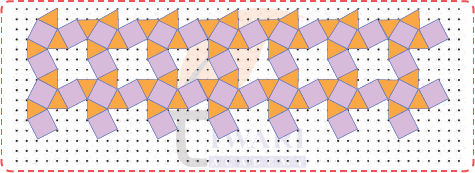
Here is a tiling pattern made using two different shapes — squares and triangles. Are the triangles equilateral? Why or why not?

See AnswerAn equilateral triangle means all three sides are equal and all angles are 60°. In the tiling pattern, the triangles placed with the squares do not look equilateral, because their sides are not all equal. Two of it’s sides are equal to side of square but the third side is smaller.

What shapes are coming together at the marked points?
See AnswerAt the marked points, we can see a square and two triangles touching each other. So, three shapes meet:
• 1 square
• 2 triangles

Are the same set of shapes coming together at these points?
Continue the pattern and colour it appropriately.
See AnswerYes. At each marked point in the pattern, the same set of shapes (1 square + 2 triangles) meet. This shows the pattern is regular and repeating, which is important in tessellation.

Create similar patterns using other cutouts of shapes.
Answer:

Page 97

What geometrical shapes can you make by fitting 2 of these triangles together? Trace the shapes you created.

Answer:
The most common shapes we can create: Parallelogram, Triangle, Rectangle and Kite.

1. How many different types of triangles can you make?
Now, observe and measure the sides of these triangles. What do you notice?
See AnswerWe can make 2 different triangles.
After measuring the sides, we find that these are isosceles triangles.

Trace the isosceles triangles on a paper and cut them out. Fold them in half. What do you notice about their angles?
2. Is it possible to make a triangle where all three sides are equal (equilateral triangle)?
See AnswerNo, it is not possible to make an equilateral triangle with these two parts.

3. Is it possible to make a triangle where all three sides are unequal?
See AnswerA single part is in the form of a scalene triangle but joining two parts not forming a triangle whose all sides are unequal.

Page 97

Try This

Cut the equilateral triangle provided at the end of the book. Check if all the angles of an equilateral triangle are equal—just like you did with the isosceles triangle.
Equilateral triangles have equal angles.
Now, cut the equilateral triangle in half. How many sides of each new triangle are equal?
See AnswerYes, all the angles of an equilateral triangle are equal.
When we cut the equilateral triangle in half, we will see that all the sides are unequal.

Triangles that have no equal sides are called scalene triangles.
Check in scalene triangles whether any two or more angles are equal?
See AnswerAll the angles are different in scalene tringle we obtain by cutting equilateral triangle in half.

4. How many different 4-sided shapes (quadrilaterals) can you make?
See AnswerWe can make three different quadrilaterals.

5. Measure the sides of each of these two quadrilaterals A and B. What do you notice?
Are there any pairs of sides that are equal? Which pairs are equal— adjacent or opposite?
See AnswerIn both shapes A and B, the opposite sides are equal (the top and bottom are equal, the left and right are equal).
In the first figure, kite, adjacent sides are equal.

6. In the grid given below, draw two different kites and parallelograms each.

Answer:

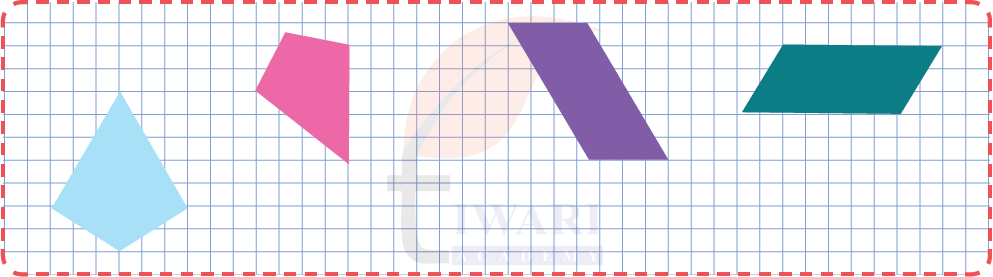
7. Now, use 3 triangles from the rhombus to form shapes. How many sides do each one of them have?
Answer:

8. Which of these shapes can be made with all 4 pieces? Try and find out.
(a) Square
(b) Rectangle
(c) Triangle
(d) Pentagon (5-sided)
(e) Hexagon (6-sided)
(f) Octagon (8-sided)
See Answer(a) Square
If you divide a rhombus into four triangles using its diagonals, you get four identical right triangles. With these four pieces:
(a) Square: Not possible (unless the rhombus was already a square).
(b) Rectangle: Possible. Two triangles can form a rectangle, and combining two rectangles gives a larger rectangle.
(c) Triangle: Not possible—four pieces cannot be arranged into a perfect triangle.
(d) Pentagon (5-sided): Cannot be formed.
(e) Hexagon (6-sided): Possible, by arranging the four triangles with their hypotenuses facing outward.
(f) Octagon (8-sided): Not possible with just four pieces.

Page 99

Tangram

Look at the tangram set given at the end of your textbook. Cut out all the shapes. Name them.

(a) How are they same or different from each other?
See AnswerShape 1, 2, 3, 5 and 6 are triangles. Out of these shapes 2 and 3 are equal and shapes 1 and 5 are equal. Shape 4 is a square and shape 7 is a parallelogram.

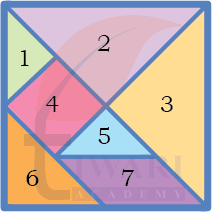
(b) What do you notice about the angles of each of the shapes?
See AnswerIn shape 2, 3 and 6 only two angles are equal where as in shape 1, 5 and 4 all angles are equal. In shape 7 opposite angles are equal.

(c) What do you notice about the sides of each of the shapes?
See AnswerIn shape 2, 3 and 6 only two sides are equal where as in shape 1, 5 and 4 all sides are equal. In shape 7 opposite sides are equal.

Page 100

Which Shape Am I?

Match the statements with appropriate shapes. Do some of them describe
more than one shape?

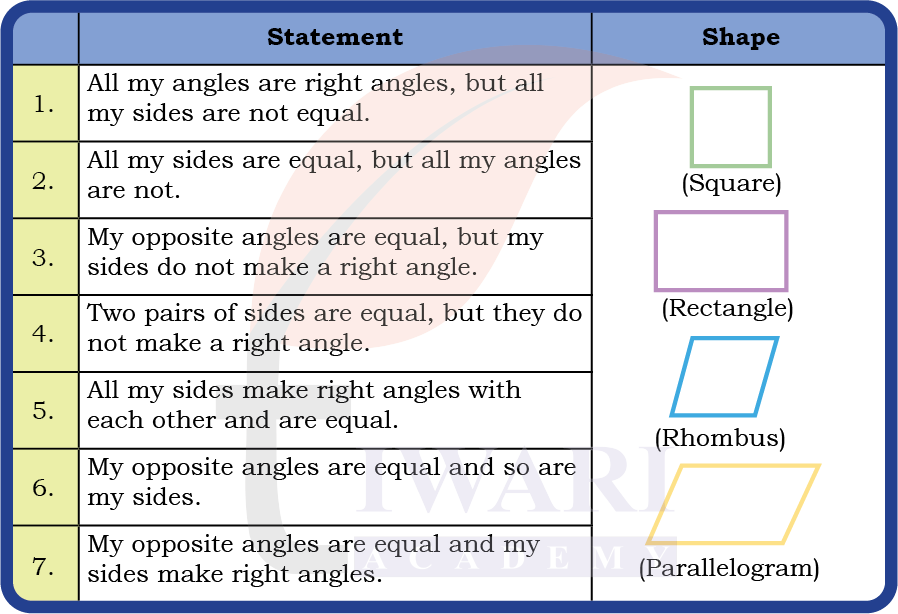
Answer:

Page 101

Play with Circles

Do you remember a circle?
(a) Draw a circle with a compass and mark its centre.
(b) Draw its diameter. Mark the endpoints of the diameter.
(c) Draw another diameter of the circle and mark the endpoints.
(d) Now join the four points.

What shape is formed? Check the sides of the quadrilateral and the angles obtained.
See AnswerThe opposite sides and angles are equal. All angles are right angles.

Try with a different pair of diameters.
What do you notice about the shape that is formed?
See AnswerEvery time we get a rectangle.

Is it possible to create a 4-sided shape other than a rectangle through this process?
See AnswerWe can create a rectangle only with this process.

Page 102

Cube Connections

1. Here are three views of a cube. Can you draw them on the net in the
correct order?

Answer:

2. Here are some big solid cube frames. How many small cubes have been removed from each cube?

See AnswerCount the number of empty spaces in each frame cube.
(a) 7 cubes are removed.
(b) 32 cubes are removed.
(c) 81 cubes are removed.

3. Nisha has glued 27 small cubes together to make a large solid cube. She paints the large cube red. How many of the original small cubes have—
(a) three faces painted red? ______ (b) two faces painted red? ______
(c) one face painted red? ______ (d) no faces painted red? ______
See Answer(a) Three faces painted: These are the corner cubes. There are 8 corners.
(b) Two faces painted: These are the edge cubes, but not the corners. There are 12 edges, each with 1 cube in the middle. 12 x 1 = 12.
(c) One face painted: These are the center of each face. There are 6 faces, each with 1 center cube. 6 x 1 = 6.
(d) No faces painted: This is the single cube hidden right in the very center of the big cube. There is only 1.

Puzzle

Tanu arranged 7 shapes in a line. She used 2 squares, 2 triangles, 1 circle, 1 hexagon and 1 rectangle.
Find her arrangement using the following clues:
(a) The square is between the circle and the rectangle.
(b) The rectangle is between the square and the triangle.
(c) The two triangles are next to the square.
(d) The hexagon is to the right of the triangle.
(e) The circle is to the left of the square.
See Answer(a) The square is between the circle and the rectangle: So it must be Circle, Square, Rectangle or Rectangle, Square, Circle.
(b) The rectangle is between the square and the triangle: So now it’s Circle, Square, Rectangle, Triangle or Triangle, Rectangle, Square, Circle.
(c) The two triangles are next to the square: We already have one triangle after the rectangle. The other triangle must be on the other side of the square. So it becomes Triangle, Circle, Square, Rectangle, Triangle. But, the circle is to the left of the square (from clue e), so it must be: Triangle, Circle, Square, Rectangle, Triangle
(d) The hexagon is to the right of the triangle: Our last shape is a triangle, so put the hexagon after it. We also have one rectangle and one hexagon left to place. Our sequence now is: Triangle, Circle, Square, Rectangle, Triangle, Hexagon.
(e) The circle is to the left of the square: … Circle, Square …
We have used all shapes: 2 squares (we used 1), 2 triangles (used both), 1 circle (used), 1 hexagon (used), 1 rectangle (used). We are missing one square! We must have two squares. The only place it can fit is at the very end.
Final Arrangement (from left to right):
Triangle, Circle, Square, Rectangle, Triangle, Hexagon, Square.

Page 103

Icosahedron and Dodecahedron

What do these names mean? Once you count their faces, you will know.
See AnswerIcosahedron: It is a geometric solid with 20 faces, typically shaped as equilateral triangles in the case of a regular icosahedron.
Dodecahedron: It is a three-dimensional shape having twelve plane faces, in particular a regular solid figure with twelve equal pentagonal faces.

What shapes do you see in an icosahedron and a dodecahedron?
Icosahedron: …….. Dodecahedron: ……..
See AnswerIcosahedron: All the faces are triangles. It looks like it’s made of lots of little pyramids.
Dodecahedron: All the faces are pentagons (5-sided shapes, like the black parts on a soccer ball.

Do all the faces look the same?
Icosahedron: …….. Dodecahedron: ……..
See AnswerIcosahedron: Yes, Every single face is an identical triangle.
Dodecahedron: Yes, Every single face is an identical pentagon.

How many faces meet at a vertex (point)?
Icosahedron: …….. Dodecahedron: ……..
See AnswerIcosahedron: 5 triangles meet at each vertex.
Dodecahedron: 3 pentagons meet at each vertex.

Do the same number of faces meet at each vertex?
Icosahedron: …….. Dodecahedron: ……..
See AnswerIcosahedron: Yes, At every single corner, exactly 5 triangles meet.
Dodecahedron: Yes, At every single corner, exactly 3 pentagons meet.

How many edges do you see?
Icosahedron: …….. Dodecahedron: ……..
See AnswerThe edge is the line where two faces meet.
Icosahedron: It has 30 edges.
Dodecahedron: It has 30 edges.

How did you count them such that you do not miss out any edge or count
an edge twice?
See AnswerFor the Icosahedron: We can see that each of the 20 triangles has 3 sides,
so 20 x 3 = 60.
But each edge is shared by 2 triangles. So, we counted every edge twice. The real number is 60 ÷ 2 = 30 edges.
For the Dodecahedron: Each of the 12 pentagons has 5 sides,
so 12 x 5 = 60.
Again, each edge is shared by 2 pentagons.
So, 60 ÷ 2 = 30 edges.

Can you think of any other solid shapes that have faces that look the same?
See AnswerYes we can think of other solid shapes that have faces that look the same are mentioned below:
Cube (or Hexahedron): All faces are identical squares.
Tetrahedron: A pyramid with 4 identical triangular faces.
Octahedron: Looks like two pyramids stuck together. It has 8 identical triangular faces.
These shapes, along with the Icosahedron and Dodecahedron, are called the Platonic Solids.

Do the same number of faces meet at each common vertex? ………..
See AnswerYes, same number of identical faces meet at every single vertex.

You can also build some 3-D shapes using straws or ice-cream sticks and
clay or play dough.
Which shapes did you make?

See AnswerWith straws and clay, we can make:
Cubes and cuboids (like a box).
Pyramids with a square base (square pyramid) or a triangular base (tetrahedron).
Triangular prisms (like a tent shape).