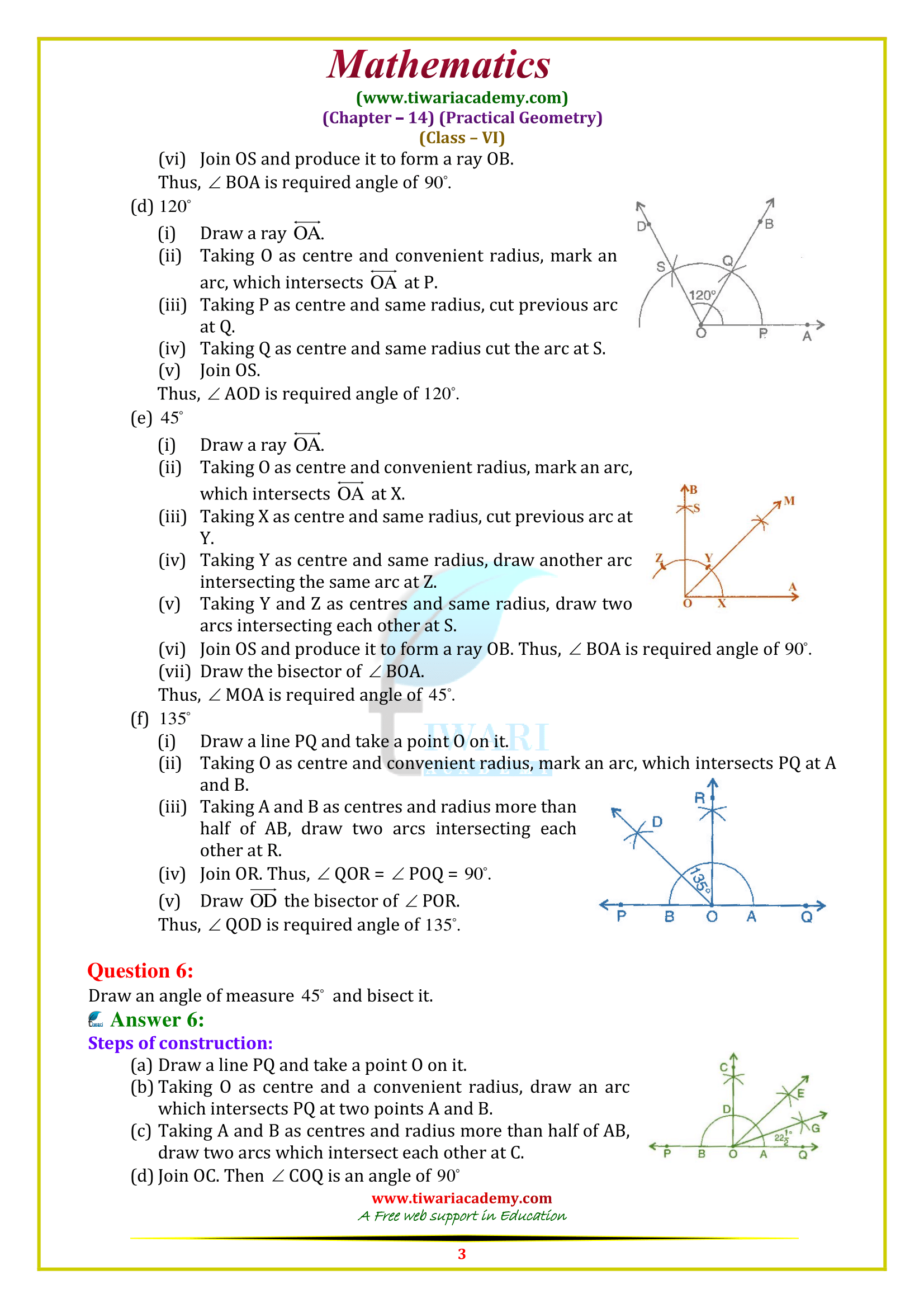
NCERT Solutions for Class 6 Maths Chapter 14 Exercise 14.6 in Hindi and English Medium updated for CBSE and State Board. Browse the latest Class 6 Maths NCERT Solutions for Ch 14 Ex 14.6 on Practical Geometry, available at Tiwari Academy in Hindi & English, optimized for CBSE and state board sessions.
6th Maths Exercise 14.6 Solutions in Hindi and English Medium
Class 6 Maths Chapter 14 Exercise 14.6 Solution
Class VI Mathematics NCERT (https://ncert.nic.in/) Textbook Ex. 14.6 Practical Geometry solution in English Medium and Hindi Medium updated for CBSE and state board students. All the contents are designed and prepared as per the latest CBSE Syllabus 2025-26. In Class 6 math exercise 14.6 deals with the questions related to angle formation and their bisectors. Step by step solutions are given in PDF and videos solutions with complete explanation.
| Class: 6 | Mathematics |
| Chapter: 14 | Exercise: 14.6 |
| Topic: | Practical Geometry |
| Medium: | Hindi and English Medium |
Class 6 Maths Chapter 14 Exercise 14.6 Solution in Videos
Construction of Angles of Special Measures
There are some elegant and accurate methods to construct some angles of special sizes without the use
I. To Construct an Angle of 60°
We take the following steps for this construction:
- Draw a ray BC.
- With B as centre and any suitable radius draw an arc above BC cutting BC at R.
- With R as centre and same radius cut the arc at S.
- Join BS and produce it to A.
- Then angle ABC is the required angle of 60°.
II. To construct an Angle of 30°
Observe that 30° = ½ × 60°.
We therefore, follow the procedure of bisecting a given angle learnt in previous section to get the required angle. Thus, to construct an angle of 30°, we proceed as follows:
Step-1: Draw an angle ABC = 60° as done above.
Step-2: Bisect angle ABC.
Step-3: Then angle RBC = 30° and also angle ABR = 30°.
III. To Construct an Angle of 90°
We take the following steps for this construction:
- Draw a ray BC.
- With B as centre and any suitable radius draw an arc cutting BC at D.
- With D as centre and same radius cut the arc at E and then with E as centre and the same radius cut the arc again at F.
- With E and F as centres and any suitable radius draw arcs cutting each other at P.
- Join BP and produce to A. Then angle ABC is the required angle, i.e., 90°.
IV. To Construct an Angle of 45°
We take the following steps for this construction:
(i) Draw an angle ABC = 90°.
(ii) With D as centre and radius more than half of DE draw an arc.
(iii) With G as centre and same radius as above, draw another arc cutting the first arc at H.
(iv) Join BH and produce to M.
Then angle CBM is the required angle of 45° and also angle MBA is 45°.
Class 6 Maths Exercise 14.6 Important Questions
What are the types of angles?
Different Types of Angles:
(i) Zero Angles.
(ii)Acute Angles.
(iii)Right Angles.
(iv)Obtuse Angles.
(v)Straight Angles.
(vi)Reflex Angles.
(vii)Complete Angle.
What are standard angles?
Trigonometric ratios are Sine, Cosine, Tangent, Cotangent, Secant and Cosecant. The standard angles for these trigonometric ratios are 0°, 30°, 45°, 60° and 90°. These angles are most commonly and frequently used in trigonometry.
How do you construct a 120 angle?
Constructing a 120° Angle: 120° angle can be constructed using the logic that 60° + 120° = 180°. Thus, we can understand that in order to construct 120° we can construct 60° angle and then further extend one of its arms.
V. To Construct an Angle of 120°
We take the following steps for this construction:
Step-1: Draw a ray BC.
Step-2: With B as centre and any suitable radius draw an arc cutting BC at D.
Step-3: With D as centre and same radius cut off the arc first at E and then with E as centre cut off the arc at another point F.
Step-4: Join BF and produce it to A. then angle ABC is the required angle of 120°.
What are the main points that students study in exercise 14.6 of 6th standard Maths?
The main points that students study in exercise 14.6 of 6th standard Maths are:
1. Angles
2. Constructing an angle of a given measure
3. Constructing a copy of an angle of unknown measure
4. Bisector of an angle
5. Angles of special measures
Which questions of exercise 14.6 of 6th standard Maths are more important?
Exercise 14.6 of grade 6th Maths has nine questions. Questions 4, 5, 8, and 9 of exercise 14.6 are the best questions. These questions are important also and have a chance to come in the school exams.
Is exercise 14.6 of class 6th Maths easy to understand and solve?
Exercise 14.6 of class 6th Maths is quite easy to understand and solve. This exercise is enjoyable and logical. Once students understand how to construct angles, then they rapidly solve this exercise.
Can students complete exercise 14.6 of class 6th Maths in 1 day?
No, students can’t complete exercise 14.6 of class 6th Maths in 1 day. Students require at least 3 days to finish exercise 14.6 of class 6th Maths if they give at least 1-2 hours per day to this exercise because exercise 14.6 of class 6th Maths has 9 questions and no example. This time also depends on the student’s working speed, efficiency, ability, etc.