NCERT Solutions for Class 6 Maths Chapter 3 Exercise 3.3 in Hindi and English Medium updated and modified for session 2024-25. Get here the modified format of question answers and solutions of ex. 3.3 class 6th Maths as per given in latest NCERT book for academic year 2024-25.
6th Maths Exercise 3.3 Solution in English and Hindi Medium
Class 6 Maths Chapter 3 Exercise 3.3 Solution
Class VI Mathematics textbook Ex. 3.3 of chapter 3 Playing with Numbers in Hindi Medium and English Medium updated for new CBSE Session 2024-25. Videos solution of all the questions of 6th Maths NCERT exercise 3.3 is also given question by question. PDF solutions and NCERT Books for 6th standard are also available in Hindi and English Medium.
| Class: 6 | Mathematics |
| Chapter: 3 | Exercise: 3.3 |
| Chapter Name: | Playing with Numbers |
| Medium: | Hindi and English Medium |
| Content Mode: | Text and Videos Format |
| Academic Session: | 2024-25 |
Prime Factorization
When we express a number as a product of its factors, we say that we have the number. For example, the number 24 can be factorized as:
- (i) 24 = 2 × 12
- (ii) 24 = 3 × 8
- (iii) 24 = 4 × 6
- (iv) 24 = 2 × 2 × 2 × 3
These factorizations are of different types. In the first and second factorizations, one factor is prime and the another factor is a composite number. In third factorization, both the factors are composite numbers. However, in fourth factorization, all the factors are prime numbers.
The process of expressing a given number as a product of prime factors is called prime factorization of the given number.
From the utility point of view, it is the prime factorization which is important than any other factorization. A number may not have a factorization with one or more composite factors, but it always has a prime factorization. Numbers 19 or 35 have no factorization in which a composite factor occurs. But they do have a prime factorization.
For example, 19 = 19 × 1 and 35 = 7 × 5.
Factorize 468 into prime factors. We use the division method as shown on the right:
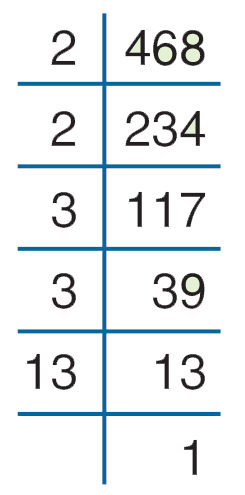
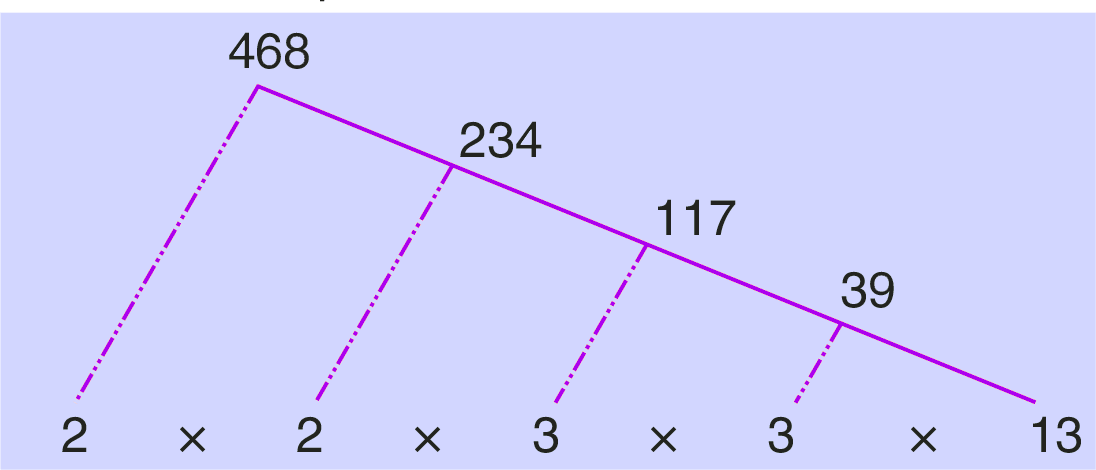
We can write, 468 = 2 × 2 × 3 × 3 × 13. Thus, the prime factorization of 468 is 2 × 2 × 3 × 3 × 13. The process can also be depicted in factor tree as follows: Image
Class 6 Maths Exercise 3.3 Important Extra Questions
what is prime factorization? Explain with the help of example.
Prime Factorization
When we express a number as a product of its factors, we say that we have the number. For example, the number 36 can be factorized as:
36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3
Write the smallest 4-digit number and express it as a product of primes.
The smallest 4-digit number is 1000. The prime factorization of this is
1000 = 2 x 500 = 2 x 2 x 250 = 2 x 2 x 2 x 125 = 2 x 2 x 2 x 5 x 25 = 2 x 2 x 2 x 5 x 5 x 5
Find the smallest number having four different prime factors.
The smallest number having four different prime factor may be 2 x 3 x 5 x 7 = 210
Fundamental Theorem of Prime Factorization
There may be several factors of a number in which one or more factors are composite as we have observed in the case of number 24. However, there is only one factorization which has all factors prime. Here, we do not distinguish between the factorization 3 × 2 × 2 × 2, 2 × 2 × 3 × 2 and 2 × 2 × 2 × 3 as we know that 2 × 3 = 3 × 2. Thus, the order of the factors in which they appear in the factorization is ignored. We thus have a property called prime factorization property or the fundamental theorem of Arithmetic, which states that Every composite number has one and only one prime factorization.
The usual method of finding the prime factors of a number is to perform successive divisions, the first divisor being the least prime number from the factors of that number. Study the following examples.
What will students study in exercise 3.3 of grade 6 Maths?
In exercise 3.3 of grade 6th Maths, students will study the following topics:
Tests for Divisibility of Numbers:
- Divisibility by 10
- Divisibility by 5
- Divisibility by 2
- Divisibility by 3
- Divisibility by 6
- Divisibility by 4
- Divisibility by 8
- Divisibility by 9
- Divisibility by 11
How many problem sums are there in exercise 3.3 of class 6 Maths?
Exercise 3.3 class 6th Maths has 6 questions and no examples. This exercise is not lengthy. This exercise is short. In all problems of exercise 3.3, students use divisibility tests to solve the problems of exercise 3.2.
Can students complete exercise 3.3 of class 6th Maths in 1 day?
No, students can’t complete exercise 3.3 of class 6th Maths in 1 day. Students require at least 2 days to finish exercise 3.3 of class 6th Maths if they give at least 1 hour per day to this exercise because exercise 3.3 class 6th Maths has 6 questions and no example. This time also depends on the student’s working speed, efficiency, capability, etc.
How many questions of exercise 3.3 of 6th Maths are considered significant for exams?
Exercise 3.3 class 6th Maths has 6 questions and no examples. All questions of this exercise are logical and important but, some questions of this exercise are most important which teacher can give in the exams. These questions are questions 5 and 6.