NCERT Solutions for Class 6 Maths Chapter 3 Exercise 3.4 in Hindi and English Medium modified and updated for academic year 2025-26 Exams. The solutions of ex. 3.4 of class 6 Mathematics are revised according to new syllabus and latest NCERT textbook issued for session 2025-26.
6th Maths Exercise 3.4 Solution in Hindi and English Medium
Class 6 Maths Chapter 3 Exercise 3.4 Solution
Class VI Maths NCERT Book Ex. 3.4 of ch 3 Playing with Numbers updated for 2025-26 CBSE Board and State board exams free to download in PDF. All the NCERT Textbook of 6th standard questions are solved in Hindi and English Medium explaining properly all the formulae. Language of solution is kept too easy to understand.
| Class: 6 | Mathematics |
| Chapter: 3 | Exercise: 3.4 |
| Chapter Name: | Playing with Numbers |
| Medium: | Hindi and English Medium |
| Content: | NCERT Exercise Solutions |
| Content Type: | Text and Videos Online |
Highest Common Factor
The Highest Common Factor of two or more given numbers is the greatest out of all their common factors. It is written as HCF. Highest common factor is also known as greatest common divisor (GCD).
For example, let us find the HCF of 28 and 32.
All the factors of 28 are 1, 2, 4, 7, 14, 28. All the factors of 32 are 1, 2, 4, 8, 16, 32.
Common factors of 28 and 32 are 1, 2, 4. Out of these, 4 is the greatest.
Thus, the HCF of 28 and 32 is 4.
We can find HCF without listing the factors, by the following methods:
- (i) Prime Factorization Method
- (ii) Continued Division Method
Class 6 Maths Exercise 3.4 Important Questions
Find the HCF of 144 and 180 by prime factorization method.
Resolving each of the given numbers into prime factors, we get:
144 = 2 × 2 × 2 × 2 × 3 × 3 and 180 = 2 × 2 × 3 × 3 × 5.
Common factors are 2 and 3. The smallest power of 2 is 2 and that of 3 is also 2. 2 2
HCF of 144 and 180 is 2 × 3 = 4× 9 = 36.
Find the HCF of 60, 72 and 102 by prime factorization method.
Resolving each of the given numbers into prime factors, we get:
60 = 2 × 2 × 3 × 5; 72 = 2 × 2 × 2 × 3 × 3; 102 = 2 × 3 × 17
Common factors are 2 and 3. The smallest power of 2 is 1 and that of 3 is also 1.
HCF of 60, 72 and 102 is 2 × 3 = 6.
Find the HCF of 84 and 126 by continued division method.
We have:
Hence, the HCF of 84 and 126 is 42.
HCF of More Than Two Numbers
Rule: If more than two numbers are given, choose any two of them and find their HCF. The HCF of this HCF and the third number gives the HCF of those three numbers. The HCF of this HCF and the fourth number gives the HCF of four numbers and so on.
Find the HCF of 221, 247 and 832.
First we find the HCF of any two numbers.
Let us take 221 and 247.
The HCF of 221 and 247 is 13.
Now, we find the HCF of 13 and 832.
The HCF of 221, 247 and 832 is 13.
Prime Factorization Method
To find the HCF of two or more numbers by prime factorization method, we take the following steps:
Step-1: Write prime factorization of each of the given numbers.
Step-2: Find the prime factors which are common to all numbers.
Step-3: Find the product of all common factors, using each common prime factor the least number of times it appears in the prime factorization of any of the given numbers. The product so obtained is the required HCF.
An Important Note
The drawback of this method is that we should know the prime factorization of the numbers involved. When the numbers are small, we can find the factorization rather easily. However, if any of the numbers is large and has large prime factors, the method is not useful.
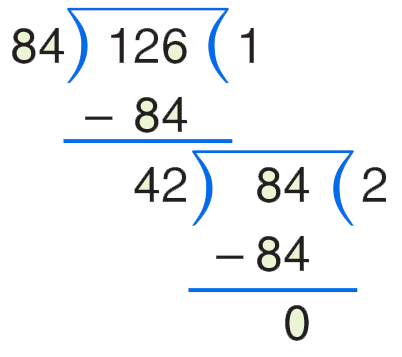
Class 6 Maths Exercise 3.4 Extra Questions with Answre
Find the greatest number which divides 532 and 1444 leaving remainders 12 and 14 respectively.
Since on dividing 532 by the required number, we get 12 as the remainder, 532 – 12 = 520 should be divisible by that number.
Similarly, 1444 – 14 = 1430 should be divisible by that number.
So, we need to find the greatest number that exactly divides 520 and 1430.
Clearly, the greatest number is the HCF of 520 and 1430.
Let us find the HCF of 520 and 1430.
The HCF of 520 and 1430 is 130.
Hence, the required number is 130.
Two tankers contain 1045 litres and 1520 litres of diesel respectively. Find the maximum capacity of a container which can measure the diesel of either tanker inexact number of times.
A container can measure 1045 litres of diesel an exact number of times if its capacity in litres is a divisor of 1045. Also, to measure 1520 litres of diesel the capacity in litres must also be divisor of 1520. Therefore, the maximum capacity of the container is the HCF of 1045 and 1520 in litres. So, first we find the HCF of 1045 and 1520.
Clearly, HCF of 1045 and 1520 is 95.
Hence, capacity of the container = 95 litres.
what do you mean by HCF?
The Highest Common Factor of two or more given numbers is the greatest out of all their common factors. It is written as HCF. Highest common factor is also known as greatest common divisor (GCD).
For example, let us find the HCF of 28 and 32.
All the factors of 28 are 1, 2, 4, 7, 14, 28. All the factors of 32 are 1, 2, 4, 8, 16, 32.
Common factors of 28 and 32 are 1, 2, 4. Out of these, 4 is the greatest.
Thus, the HCF of 28 and 32 is 4.
Find the largest number which divides 244 and 1028 leaving remainder 4 in each case.
The two numbers are 244 and 1028. You want the largest number that divides the two numbers leaving a remainder of 4 in each case.
First subtract 4 from 244 and 1028 to get
244 – 4 = 240.
1028 – 4 = 1024,
Next find the HCF of 240 and 1024. To do that find the prime factors of the two numbers:
240 = 2 x 2 x 2 x 2 x 3 x 5
1024 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Thus the HCF = 2 x 2 x 2 x 2 = 16. So the answer is 16.
Find the largest size of a square tile that can be used for paving a rectangular plot 84 m by 162 m. Also, find the number of tiles that will be needed.
Area of plot = 84 x 162 = 13608 sq. m
Now the side of one square tile is the HCF of 84 and 162.
84 = 2 x 2 x 3 x 7
162 = 2 x 3 x 3 x 3 x 3
Now HCF = 2 x 3 = 6
Now area of square tile = 6 x 6 =36 sq. m
No. of tiles = plot area / area of one tile
= 13608 /36 = 378
Continued Division Method
There is another method for finding HCF of given numbers called Continued Division Method. To find the HCF of two numbers by this method, we take the following steps:
Step- 1: Divide the larger number by the smaller number and obtain the remainder.
Step- 2: If the remainder is 0, the smaller number is the HCF. If the remainder is non-zero, divide the divisor by the remainder.
Step- 3: Repeat the process of dividing the preceding divisor by the remainder last obtained till 0 (zero) is obtained as remainder. Then the last divisor is the required HCF.
Are there any examples in exercise 3.4 of class 6 Maths?
Yes, there are two examples (examples 5, 6) in exercise 3.4 of class 6th Maths. In example 5, students have to find the common factors of given numbers. In example 6, students have to find the common multiples of the given numbers.
How many days are needed to complete exercise 3.4 of class 6 Maths?
Students need at most 2-3 days to complete exercise 3.4 of class 6th Maths if they give 1 hour per day to this exercise. This time is an approximate time and can vary.
Which questions of exercise 3.4 of class 6th Maths can students expect for exams?
In exercise 3.4 of class 6th Maths, students find out the common multiples and common factors of the given numbers. This exercise has 2 examples and 7 questions. The most important questions and examples of this exercise are questions 5, 6, 7, and example 6.
Is exercise 3.4 of 6th Maths simple to solve?
Exercise 3.4 of grade 6th Maths is not at all challenging. This exercise is overall a simple exercise. However, the difficulty level of any exercise depends on students also. Some students find exercise 3.4 easy, and some students find exercise 3.4 difficult.





