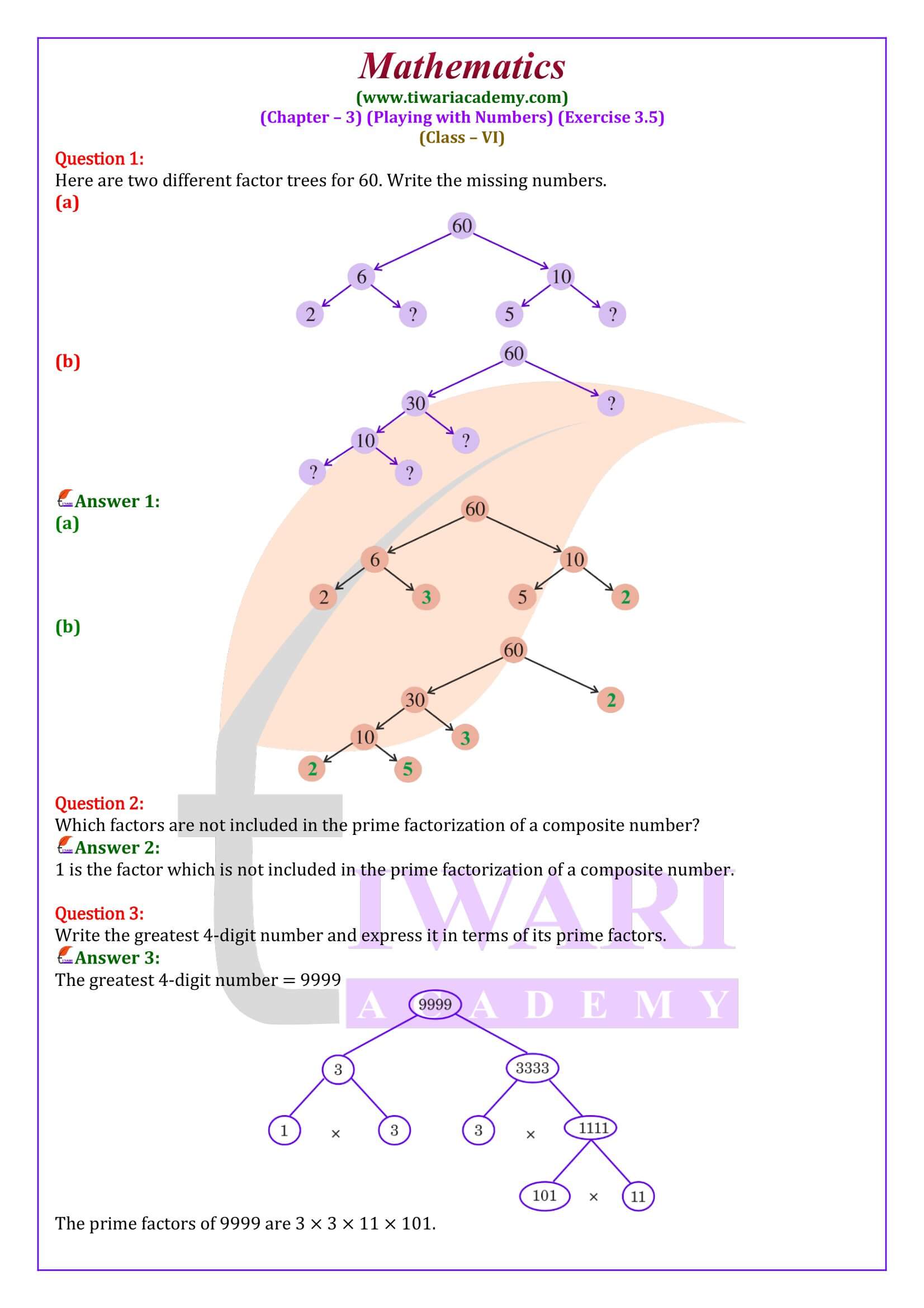
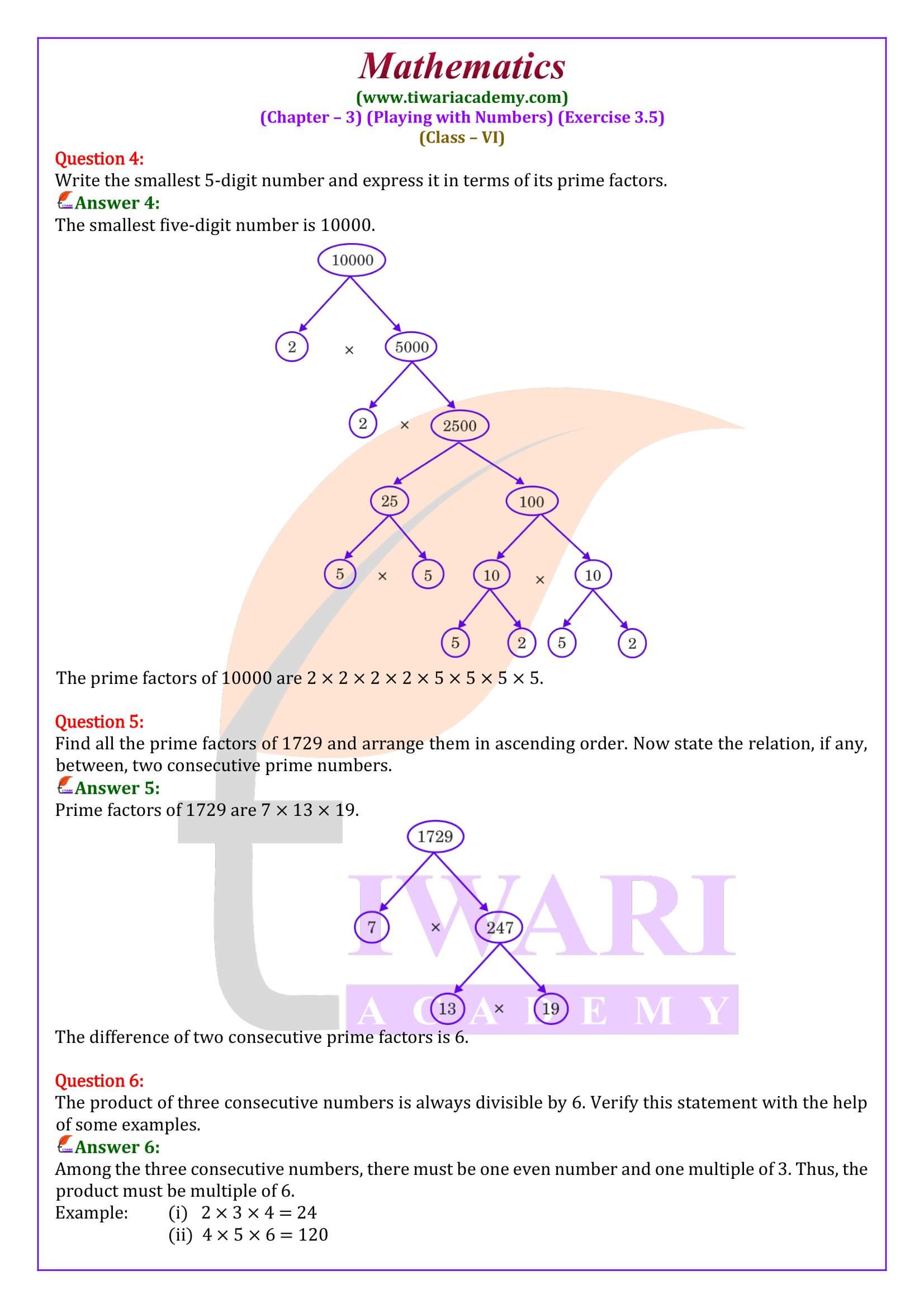
NCERT Solutions for Class 6 Maths Chapter 3 Exercise 3.5 in Hindi and English Medium updated for session 2025-26. All the questions of ex. 3.5 of 6th Maths are updated according to revised syllabus and latest NCERT books for academic year 2025-26 exams.
6th Maths Exercise 3.5 Solutions in Hindi and English Medium
Class 6 Maths Chapter 3 Exercise 3.5 Solution
Class VI NCERT Mathematics Ex. 3.5 of Playing with Numbers in PDF format Hindi and English Medium updated for CBSE session 2025-26. All the contents are free to use online without any login or password. If you feel any difficulty to access the contents, please contact us for help. We will help you as soon as possible.
| Class: 6 | Mathematics |
| Chapter: 3 | Exercise: 3.5 |
| Chapter Name: | Playing with Numbers |
| Medium: | Hindi and English Medium |
| Content: | NCERT Exercise Solutions |
| Content Type: | Online Videos and Text Foramt |
Lowest Common Multiple
The Lowest Common Multiple of two or more numbers is the smallest out of all their common multiples. In other words, the lowest common multiple of two or more numbers is the smallest number which is divisible by all the given numbers. This means that there cannot be a number divisible by the given numbers and smaller than the lowest common multiple.
We can find LCM without listing the multiples, by the following two methods:
- (i) Prime factorization method
- (ii) Common division method
Class 6 Maths Exercise 3.5 Important Questions
Find LCM of 10, 20 and 30.
Consider the numbers 10, 20 and 30.
Multiples of 10 are 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, …
Multiples of 20 are 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, …
Multiples of 30 are 30, 60, 90, 120, 150, 180, 210, …
Common multiples of 10, 20 and 30 are 60, 120, 180, ….
Hence, lowest common multiple of 10, 20 and 30 is 60.
Find the LCM of 15, 20 and 30 by division method.
We have,
| 2 | 15, 20, 30 |
| 3 | 15, 10, 15 |
| 5 | 5, 10, 5 |
| 1, 2, 1 |
LCM of given numbers = 2 × 3 × 5 × 2 = 60.
Find the least number which is divisible by 16, 24, 30 and 54.
The required number will be the LCM of the given numbers. We find the LCM of 16, 24, 30 and 54 as under
| 2 | 16, 24, 30, 54 |
| 2 | 8, 12, 15, 27 |
| 2 | 4, 6, 15, 27 |
| 3 | 2, 3, 15, 27 |
| 2, 1, 5, 9 |
Therefore, LCM of 16, 24, 30 and 54 = 2 × 2 × 2 × 3 × 2 × 5 × 9 = 2160.
Hence, the least number which is divisible by 16, 24, 30 and 54 is 2160.
Find the least number which when divided by 22, 54, 108 and 198 leaves a remainder 5 in each case.
We know that the lowest number divisible by 22, 54, 108 and 198 is their LCM.
Therefore, the required number must be 5 more than their LCM. We find the LCM of the given number as under:
| 2 | 22, 54, 108, 198 |
| 3 | 11, 27, 54, 99 |
| 3 | 11, 9, 18, 33 |
| 3 | 11, 3, 6, 11 |
| 11 | 11, 1, 2, 11 |
| 1, 1, 2, 1 |
LCM = 2 × 3 × 3 × 3 × 11 × 2 = 1188. Hence, the required number is 1188 + 5 = 1193.
LCM by Prime Factorization Method
In order to find the LCM of two or more numbers by prime factorization method, we follow these steps:
Step- 1: Write the prime factorization of each of the given numbers.
Step- 2: Find the product of all the different prime factors of the number using each common prime factor, the greatest number of times it appears in the prime factorization of any number.
The product so obtained is the required LCM of the given numbers.
Class 6 Maths Exercise 3.5 Extra Questions with Answr
what do you mean by LCM? Give one example.
The smallest positive number that is a multiple of two or more numbers.
Ex.:
LCM of 5, 10, 15
Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, etc.
Multiples of 10 are 10, 20, 30, 40, etc.
Multiples of 15 are 15, 30, 45, 60, etc.
We observe all and find least common multiple of all three is 30
Hence LCM of 5, 10 and 15 is 30.
The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 9 a.m., at what time will they change simultaneously again?
First of all, we find LCM of 48, 72 and 108
Applying division method
| 2 | 48, 72, 108 |
| 2 | 24, 36, 54 |
| 2 | 12, 18, 27 |
| 3 | 6, 9, 27 |
| 3 | 2, 3, 9 |
| 2, 1, 3 |
LCM = 2 x 2 x 2 x3 x 3 x 2 x 3 = 432
The time at which they will change simultaneously will be after 432 second means 7 minutes 12 seconds from 9 a. m.
Find the LCM of the following numbers by division method: 75, 225, 250, 525
Applying division method
| 5 | 75, 225, 250, 525 |
| 5 | 15, 45, 50, 105 |
| 2 | 3, 9, 10, 21 |
| 3 | 3, 9, 5, 21 |
| 1, 3, 5, 7 |
LCM of 75, 225, 250, 525 = 5 x 5 x 5 x 2 x 3 x 3 x 7
= 15750
LCM by Division Method
We follow steps given below to find the LCM of given numbers by division method.
- Write all the numbers in a row.
- Choose a number which divides at least two of the given numbers.
- Divide the numbers which are divisible by the number chosen in step 2 and write the quotients
- Just below them. Carry forward the numbers which are not divisible.
- Repeat step 2 and step 3 till no two of the given numbers are divisible by the same number.
- Find the product of the divisors and the undivided numbers to get the required LCM of given numbers.
How many questions and examples are there in exercise 3.5 of class 6th Maths?
In exercise 3.5 of class 6th Maths, there are 12 questions and one example (example 7). Questions of this exercise are based on the prime factorization and divisibility rules concept. Fill in the blanks, true or false (yes or no), one-word answer, MCQ, missing numbers type questions can also come from this exercise. One mark and two marks questions can be asked from this exercise.
Can students complete exercise 3.5 of class 6th Maths in 3-4 days?
Students can complete exercise 3.5 of class 6th Maths in 3-4 days or not depends on student’s working speed, efficiency, capability, and many other factors. But if they try hard to complete exercise 3.5 of class 6th Maths in 3-4 days, they can easily do that.
How difficult the exercise 3.5 of Class 6 Maths is?
Exercise 3.5 of class 6th Maths is not a very tough exercise. Some questions of this exercise are easy, and students solve them very quickly. But, in some questions students face a little problem and need the teacher’s help or parent’s help.
Which questions are the important questions of exercise 3.5 of class 6th Maths?
There are 12 questions and one example (examples 7) in exercise 3.5 of class 6th Maths. All questions of this exercise are significant for the exams. But the most important questions of this exercise are questions 1, 3, 6, 9, 10. These questions have a chance to come in the exams also.