by Shikhar Tiwari
NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.2 Exponents and Powers in Hindi and English Medium for CBSE Session 2024-25. The solutions of ex. 11.2 class VII mathematics are revised according to new syllabus and latest textbooks issued for academic year 2024-25.
Class 7 Maths Exercise 11.2 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 11 | Exercise: 11.2 |
| Topic Name: | Exponents and Powers |
| Content: | Exercise and Extra Questions |
| Academic Year: | CBSE 2024-25 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 11 Exercise 11.2 Solution
All the solutions and study material is updated according to latest NCERT Textbooks. If student feel any difficulty in PDF solutions, they may refer to video solution to understand properly. Videos related to each exercises are given separately on website as well as in app.
Class 7 Offline Maths App
Class 7 Maths Chapter 11 Exercise 11.2 Solution in Videos
Class 7 Maths App in Hindi Medium
Class 7 Maths Exercise 11.2 Important Questions
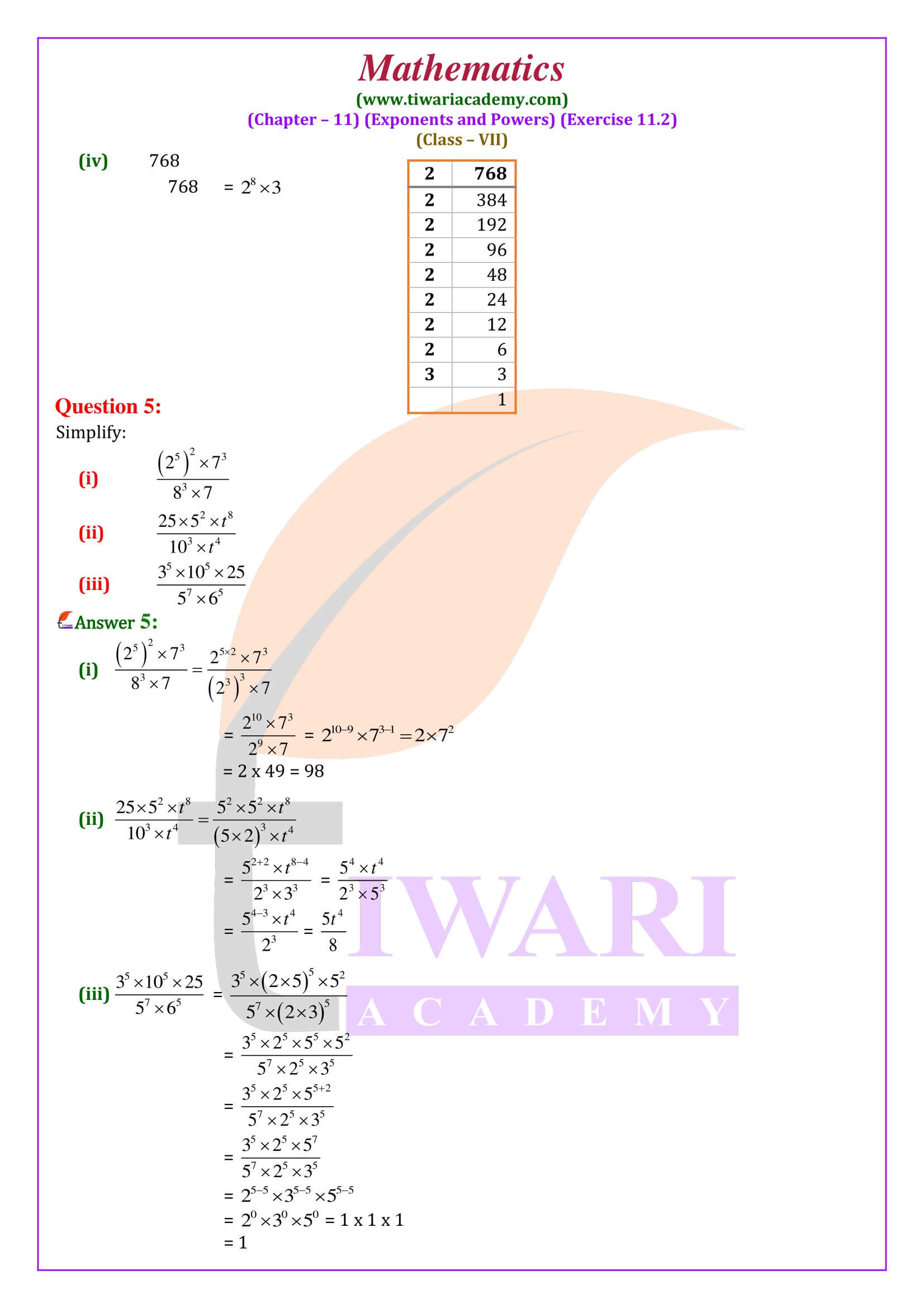
Simplify and write the answer in exponential form: (i) (62)4 (ii) (22)100 (iii) (750)2 (iv) (53)7
We have:
(i) (62)4 = 62 x 62 x 62 x 62 = 62+2+2+2 = 62×4 = 68
(ii) (22)100 = 22×100 = 2200
(iii) (750)2 = 750×2 = 7100
(iv) (53)7 = 53×7 = 521
Express the following terms in the exponential form: (i) (2 × 3)⁵ (ii) (2a)⁴ (iii) (– 4m)³
We have:
(i) (2 × 3)⁵ = (2 × 3) × (2 × 3) × (2 × 3) × (2 × 3) × (2 × 3)
= (2 × 2 × 2 × 2 × 2) × (3 × 3× 3 × 3 × 3)
= 2⁵ × 3⁵
(ii) (2a)⁴ = 2a × 2a × 2a × 2a = (2 × 2 × 2 × 2) × (a × a × a × a) = 2⁴ × a⁴
(iii) (– 4m)³ = (– 4 × m)³ = (– 4 × m) × (– 4 × m) × (– 4 × m) = (– 4) × (– 4) × (– 4) × (m × m × m)
= (– 4)³ × (m)³
Power of a Power
Consider the following
Simplify {(2)³}² = (2)³ x (2)³
Or, (2)³⁺³ = (2)⁶
Class 7 Maths Exercise 11.2 Important Questions
Simplify: (6⁻¹ – 8⁻¹)⁻¹ + (2⁻¹ – 3⁻¹)⁻¹
We have:
(6⁻¹ – 8⁻¹)⁻¹ + (2⁻¹ – 3⁻¹)⁻¹
= (1/6 – 1/8)⁻¹ + (1/2 – 1/3)⁻¹
= {(4 – 3)/24}-¹ + {(3 – 2)/6}-¹
= (1/24)⁻¹ + (1/6)⁻¹
= (24/1) + (6/1)
= 24 + 6 = 30
By what number should we multiply 3⁻⁹ so that the product is equal to 3?
Let the required number be x.
Then, 3⁻⁹ X x = 3
Or, x = 3/3⁻⁹
Or, x = 3 X 3⁹
X = 3¹⁺⁹ = 3¹⁰
Hence, the required number is 3¹⁰
By what number should we multiply (-8)⁻¹ to obtain a product equal to 10⁻¹?
Let the required number be x. Then,
Then, (-8)⁻¹ X x = 10⁻¹
Or, x = 10⁻¹/(-8)⁻¹
Or, x = -8 / 10
X = -4/5
Multiplying Powers with the Same Exponents
simplify 2³ × 3³? Notice that here the two terms 2³ and 3³ have different bases, but the same exponents.
Now, 2³ × 3³ = (2 x 2 x 2) x (3 x 3 x 3)
Or, (2 x 3) x (2 x 3) x (2 x 3)
= 6 x 6 x 6 = 6³ (Observe 6 is the product of bases 2 and 3)
In general, for any non-zero integer a
Aᵐ × bᵐ = (ab)ᵐ (where m is any whole number)
