by Tiwari Academy
NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.1 Visualising Solid Shapes in Hindi and English Medium updated for session 2024-25. The question answers and solution are revised as per the new syllabus and latest NCERT textbook published for the academic year 2024-25.
Class 7 Maths Exercise 13.1 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 13 | Exercise: 13.1 |
| Topic Name: | Visualising Solid Shapes |
| Content: | Textbook and Practice Questions |
| Academic Year: | CBSE 2024-25 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 13 Exercise 13.1 Solution
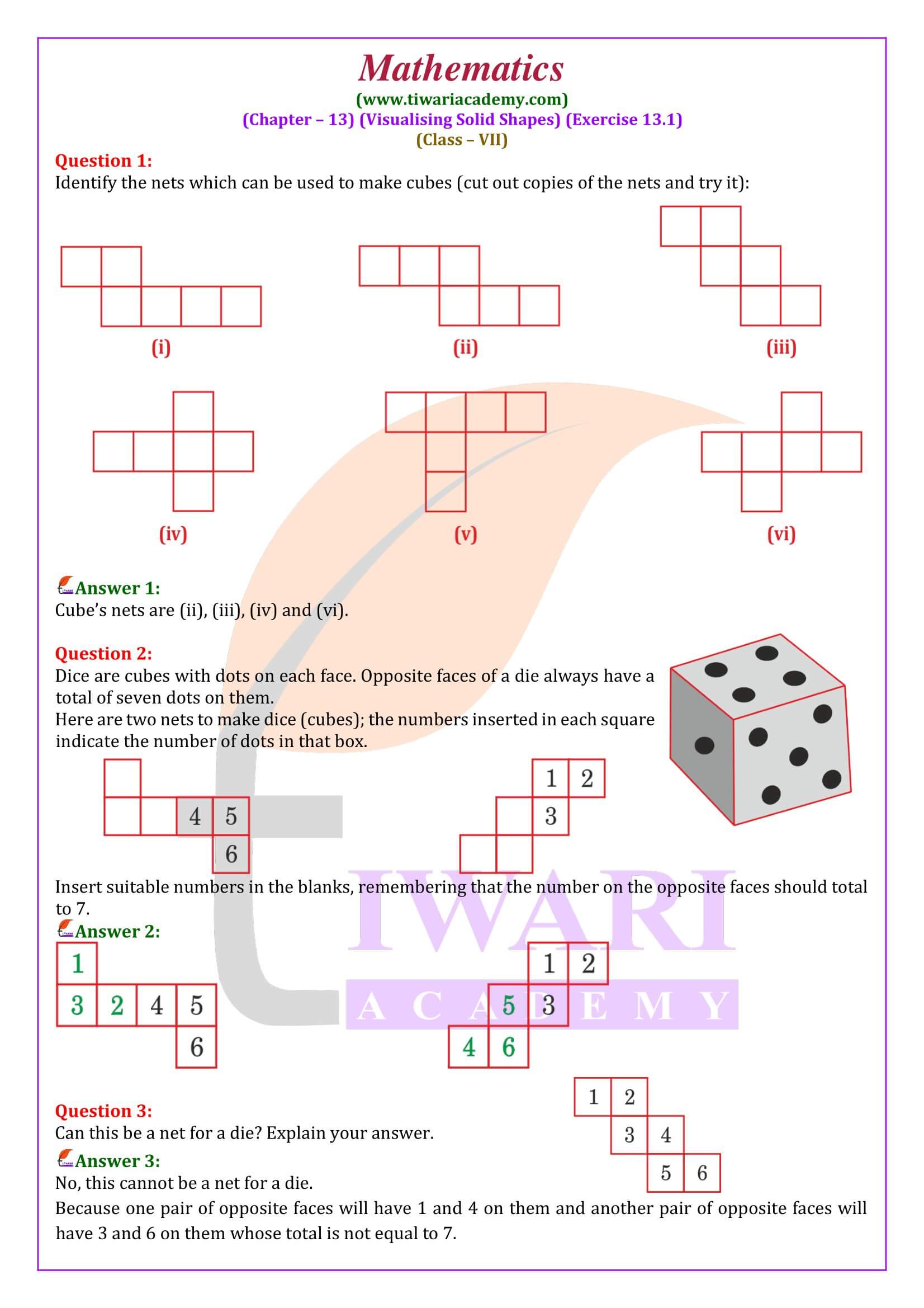
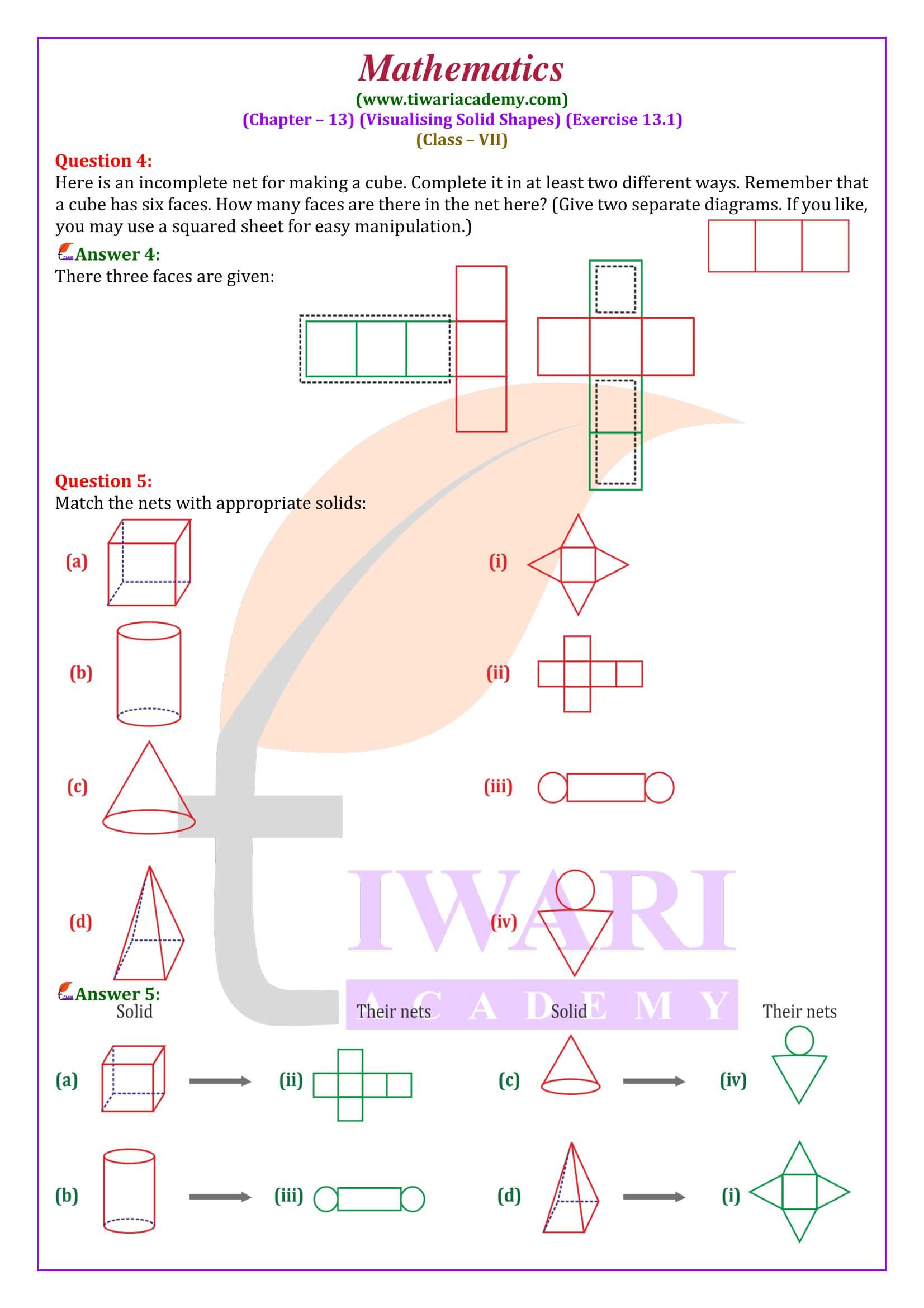
Practice all questions with the help of PDF, if still any doubt, please visit to videos. In class 7 math NCERT exercise 13.1, we will learn to observe the net of different solids. We will also try to identify the solid using their nets. Questions given in this exercise is mostly based on observation.
Free App for Grade 7 Mathematics
Class 7 Maths Chapter 13 Exercise 13.1 Solution in Videos
Class 7 Maths App in Hindi Medium
Three Dimensional Shapes
three-dimensional shapes (3D shapes) are also called the solids, which have three-dimensions namely length, width and height. 3D shapes can include both polyhedrons and curved solids.
Examples:
Cuboid, Cube, Cylinder, Cone, Sphere and Pyramid etc.
One Dimensional Figures: A line segment is one-dimensional, since it has only length.
The figures which have only length and breadth are called two dimensional (2-D) figures. A 2-D figure does not possess height.
Examples: Square, rectangle, triangle etc.
Class 7 Maths Exercise 13.1 Important Questions
What 3D shape has 1 face?
A face is a flat or curved surface on a 3D shape. For examples a cube has six faces, a cylinder has three and a sphere has just one.
How are 3D shapes used in everyday life?
We live in a three-dimensional world. Every one of us has height, width, and length. Shapes exist in our 3D world, too: game dice, cuboids, donuts, pyramids, beach balls, traffic cones. All of those are 3D shapes.
Does a cone have 1 or 2 faces?
A Face or Surface of a solid figure, can be plane or curved. So, A Cone has TWO faces, one plane face (or surface). And the other one is curved face (or surface) … (1) Plane face is circular in shape.
What is the most basic shape?
The square, circle, and triangle are the most basic shapes on Earth, supporting structures both synthetic and natural.
Solids
The objects having definite shape and size are called solids. A solid occupies a fixed amount of space.
Solids occur in various shapes, such as a cuboid, a cube, a cylinder, a cone, a sphere, etc. All solid figures have three elements faces, edges and vertices.
Cuboid
A solid bounded by six rectangular faces is called a cuboid. A cuboid has three dimensions, namely length, breadth and height. A matchbox, a chalk box, a brick, a tile, a book, an almirah, etc., are all examples of a cuboid.
Properties of Cuboid
(i) A cuboid has 6 rectangular faces. The opposite faces of a cuboid are identical.
(ii) Two adjacent faces of a cuboid meet in a line segment called an edge of the cuboid. A cuboid has 12 edges.
(iii) Three edges of a cuboid meet at a point called a vertex. A cuboid has 8 vertices.
