by Tiwari Academy
NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.2 Visualising Solid Shapes in Hindi and English Medium for CBSE Session 2024-25. The students of class 7 can get the revised solutions of ex. 13.2 mathematics here, which is based on new NCERT textbooks issued for academic year 2024-25.
Class 7 Maths Exercise 13.2 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 13 | Exercise: 13.2 |
| Chapter Name: | Visualising Solid Shapes |
| Content Mode: | Text, Images and Videos |
| Academic Year: | CBSE 2024-25 |
| Medium: | English and Hindi Medium |
Class 7 Maths Chapter 13 Exercise 13.2 Solution
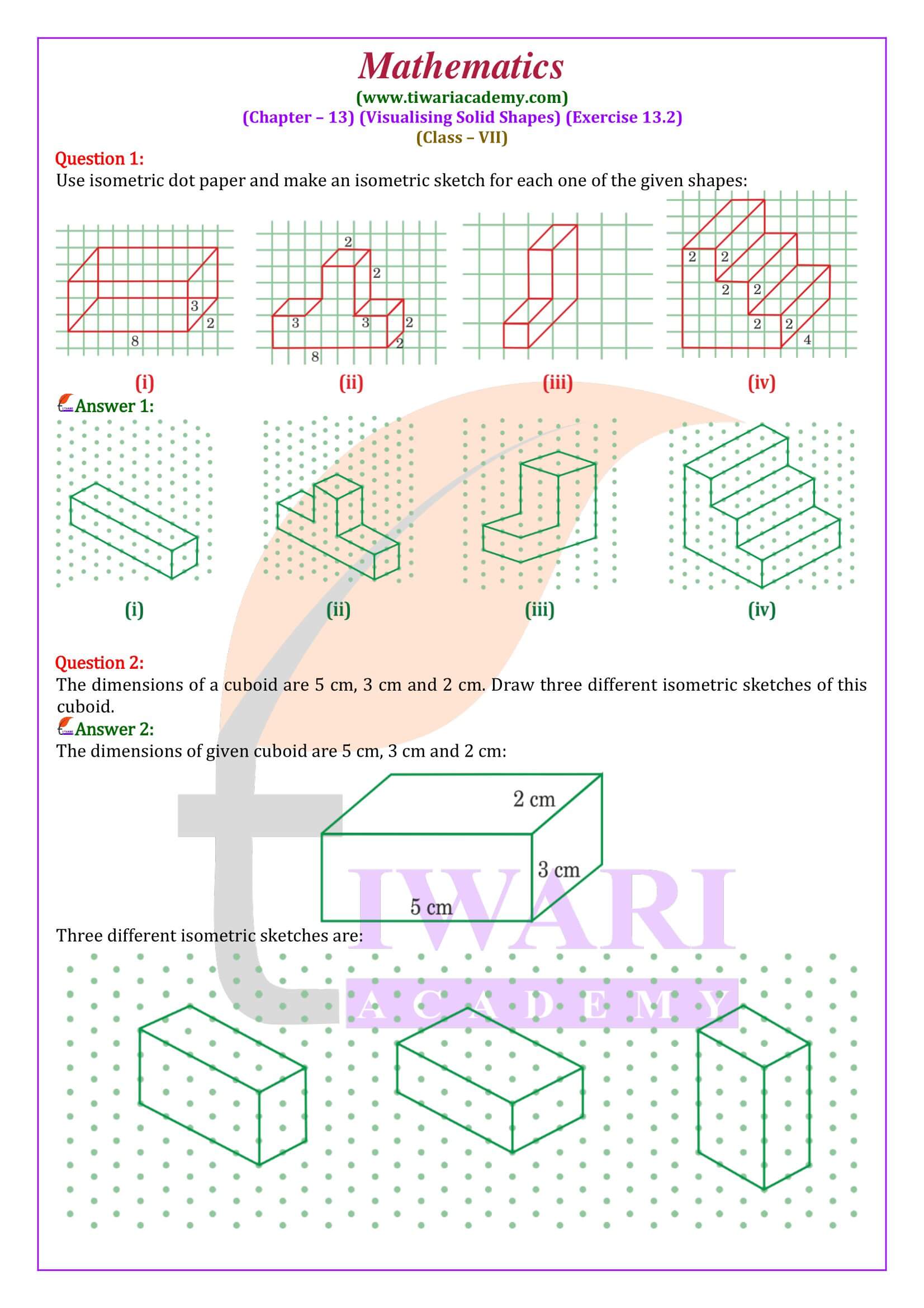
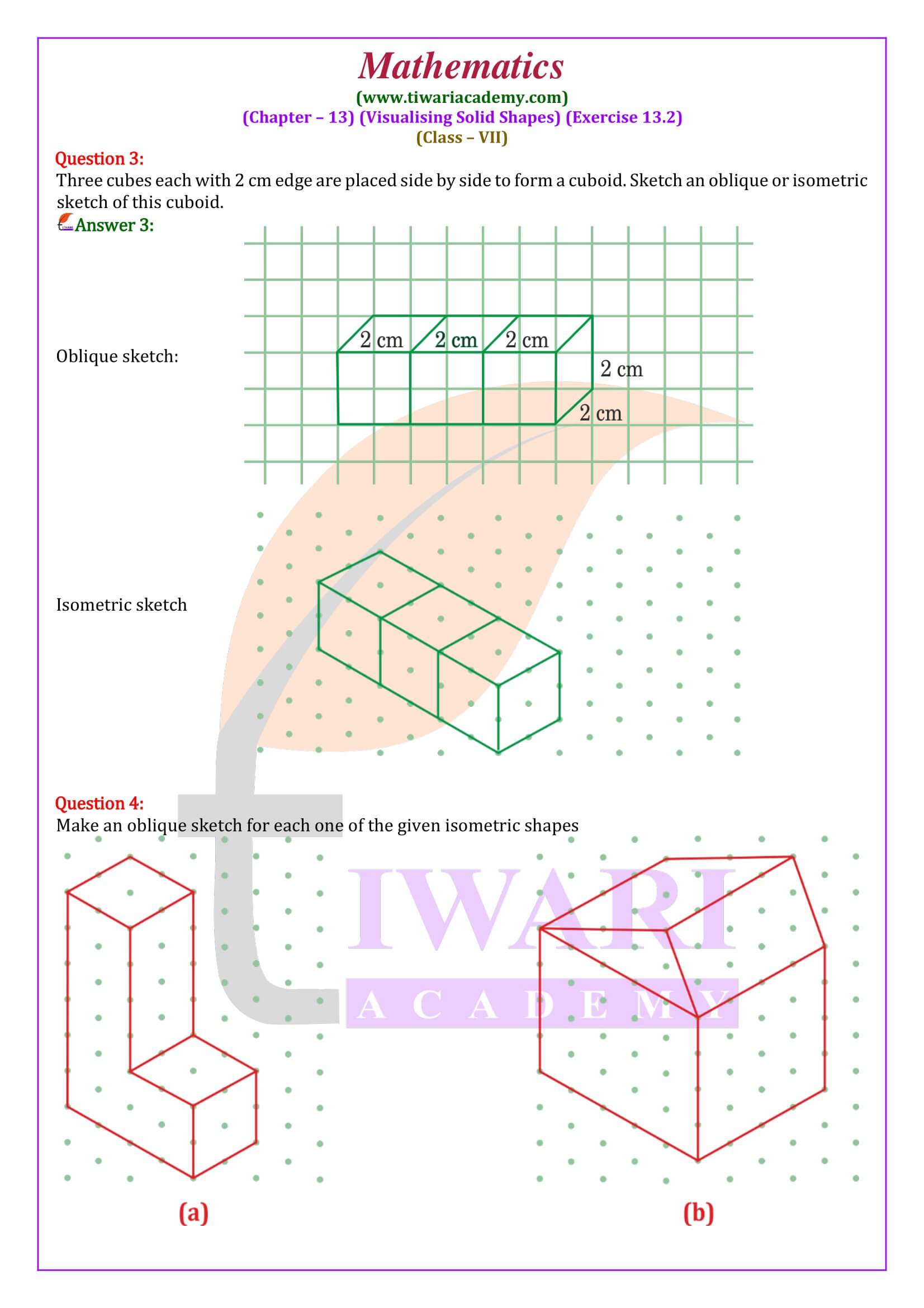
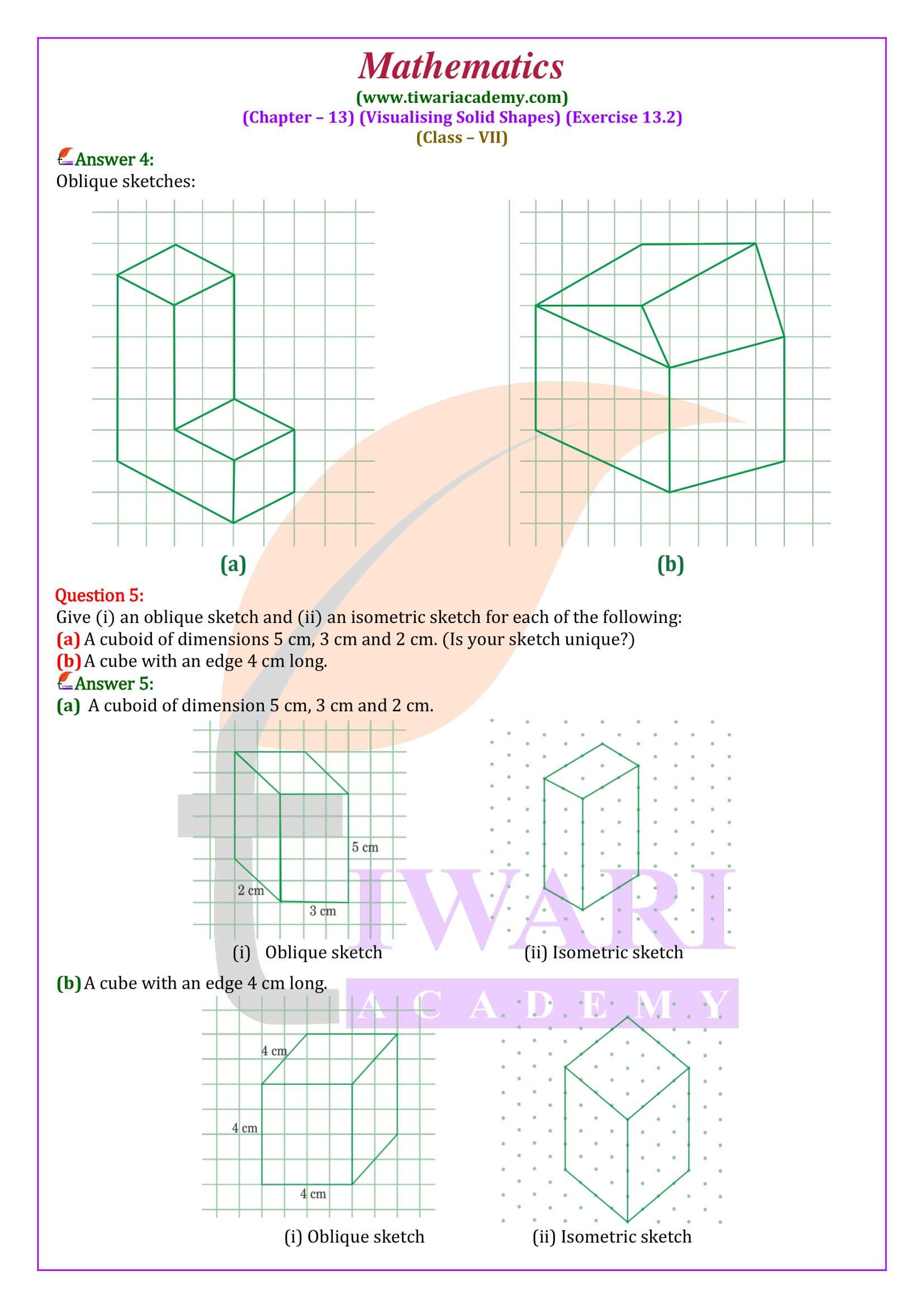
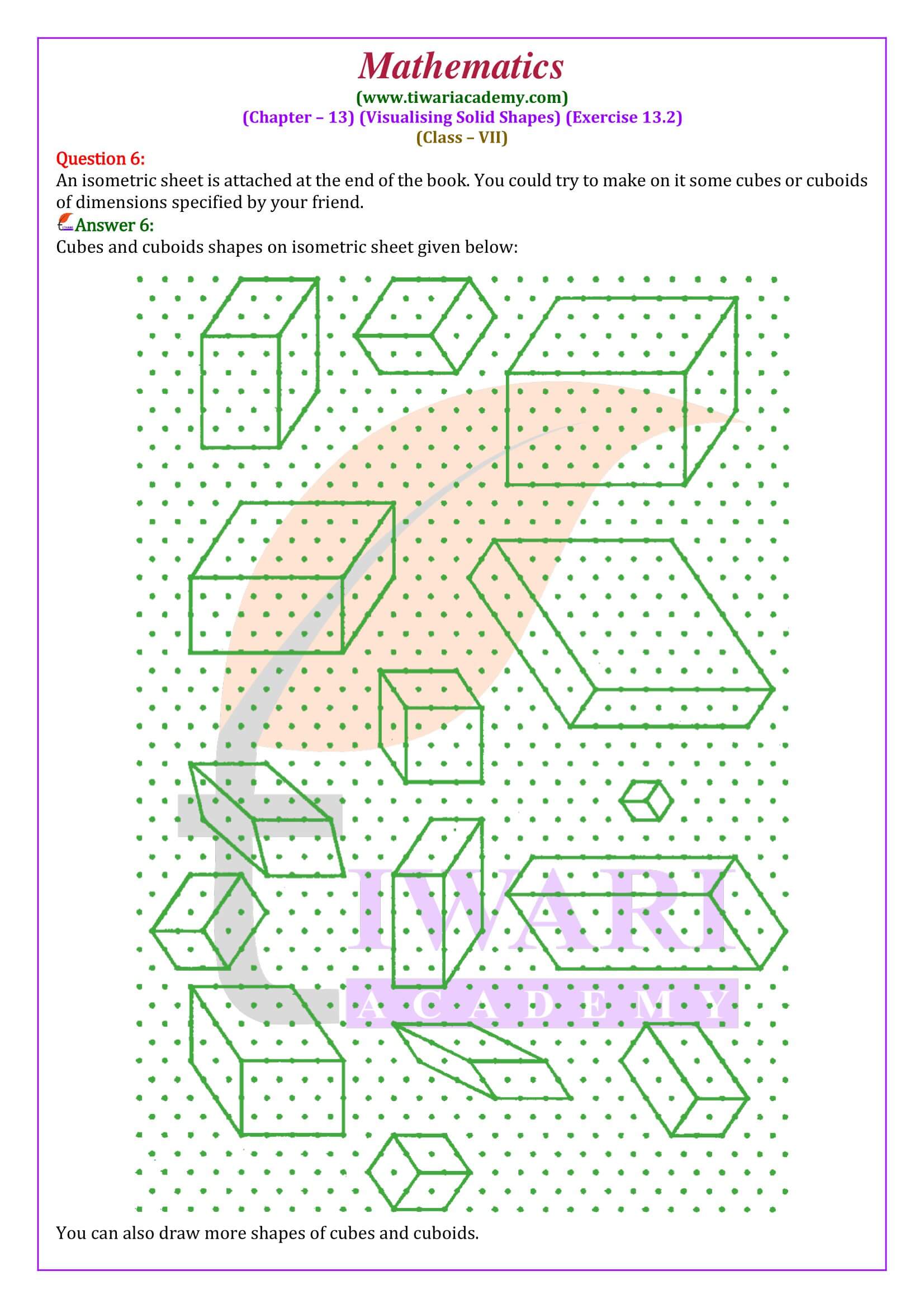
All the questions are solved properly using step by step method and explaining each terms. In class 7 mathematics NCERT exercise 13.2, we will learn to draw isometric sketch using isometric dot paper. Here, we also learn to draw several isometric sketch of the same solid object.
Offline App for Class 7 Maths
Class 7 Maths Chapter 13 Exercise 13.2 Solution in Videos
Hindi Medium app Class 7 Maths
Class 7 Maths Exercise 13.2 Extra Questions
How do you solve cube and dice problems?
Most dice are cube shaped, with the numbers 1 to 6 on the different faces.
1. Two opposite faces of the dice cannot be adjacent to each other.
2. If two dice are shown as below, and one of the two common faces (Face number 4) is in the same position, then the remaining faces will be opposite to each other.
Why does a cylinder have 2 faces?
All of these figures are curved in some way, so they have no edges or vertices. What about their faces? A sphere has no faces, a cone has one circular face, and a cylinder has two circular faces. Therefore, the number of faces increases by one from one figure to the next.
Cube
A cuboid whose length, breadth and height are all equal is called a cube. Dice, ice cubes and sugar cubes, etc., are all examples of a cube. Like cuboid, a cube has 6 faces, 12 edges and 8 vertices.
Let ABCDEFGH is a cube
(i) 6 faces of the cube are: ABCD, EFGH, ADHE, BCGF, ABFE, DCGH. Lateral faces are: ABFE, DCGH, BCGF, ADHE.
(ii) 12 edges of the cube are: AB, BC, CD, DA, EF, GH, FG, EH, CG, BF, AE, DH etc.
(iii) 8 vertices of the cube are A, B, C, D, E, F, G, H. Length, breadth and height of a cube are equal.
Cylinders
Solids like circular pillars, circular pipes, circular pencils, measuring jars, road rollers and gas cylinders, etc., are said to be in cylindrical shapes.
Class 7 Maths Exercise 13.2 Important Questions
How are cones different from cylinders?
A cone is a 3-dimensional solid object that has a circular base and a single vertex.
Cylinder: A cylinder is a 3-dimensional solid object that has two parallel circular base connected by a curved surface.
How many cones does a cylinder have?
The reason the volume of a cone involves using the fraction 1/3, is because it takes three cones to fill up a cylinder.
Can a cone and cylinder have the same volume?
In a similar way, the volumes of a cone and a cylinder that have identical bases and heights are proportional. If a cone and a cylinder have bases (shown in color) with equal areas, and both have identical heights, then the volume of the cone is one-third the volume of the cylinder.
Parts of a Cylinder
(i) A cylinder has no vertex.
(ii) A cylinder has two curved edges (C1 and C2).
(iii) A cylinder has one curved face and two flat faces (F1 and F2).
Cone
Objects such as ice-cream cone, a conical tent, a conical vessel, a clown’s cap, etc., are in the shape of a cone.
Parts of a Cone
(i) A cone has one vertex.
(ii) A cone has one curved edge.
(iii) A cone has one curved face and one flat face.
