by Tiwari Academy
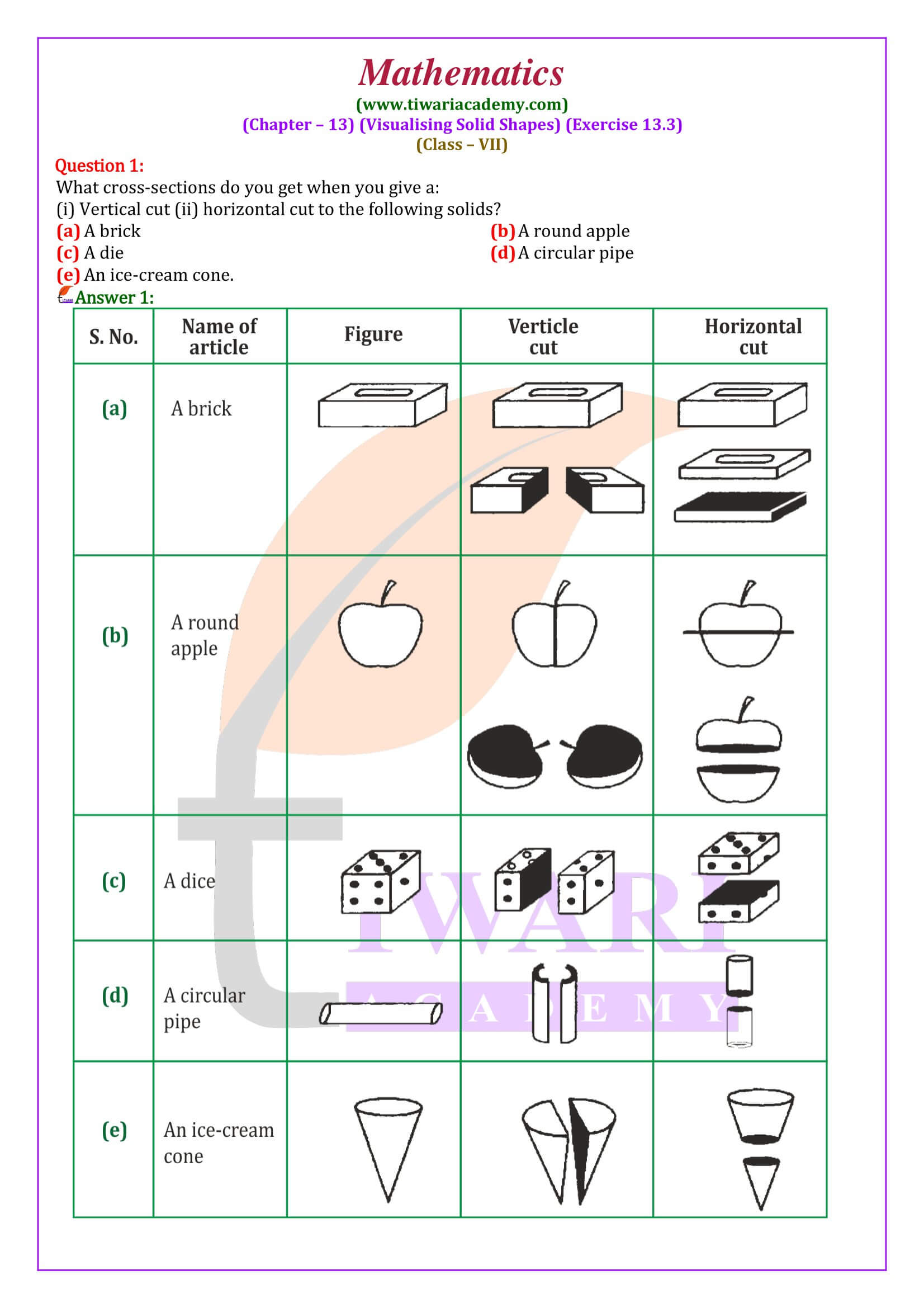
NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.3 Visualising Solid Shapes in Hindi and English Medium updated for 2024-25 exams. The solutions of ex. 13.3 class VII mathematics are revised according to rationalised syllabus and latest NCERT textbooks issued for academic session 2024-25.
Class 7 Maths Exercise 13.3 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 13 | Exercise: 13.3 |
| Topic: | Visualising Solid Shapes |
| Content Type: | PDF and Videos Solution |
| Academic Year: | CBSE 2024-25 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 13 Exercise 13.3 Solution
All the contents are based on latest NCERT Books issued for academic session 2024-25. Class 7 math exercise 13.3 is based on vertical and horizontal cross section of solid objects. In exercise 13.3, there is only one question is given, which quite easy to understand by observing only.
Class 7 Maths App in English
Class 7 Maths Chapter 13 Exercise 13.3 Solution in Videos
Class 7 Maths Hindi Medium App
Class 7 Maths Exercise 13.3 Extra Questions
What is special about a sphere?
Important Facts: A sphere is a symmetrical object. All the surface points of sphere are at equidistant from center. A sphere has only curved surface, no flat surface, no edges and no vertices.
Why is a sphere the most efficient shape?
A sphere has the lowest possible surface area required to bound any given volume. Therefore, it is the most energy-efficient configuration.
How many faces edges and vertices has a triangular pyramid?
Properties of Triangular Pyramid
It has 4 faces. The 3 side faces are triangles. The base is also a triangle. It has 4 vertices (corner points).
Sphere
An object which is in the shape of a ball is said to have the shape of a sphere.
Parts of a Sphere
(i) A sphere has no vertex.
(ii) A sphere has no edge.
(iii) A sphere has a curved surface.
Class 7 Maths Exercise 13.3 Important Questions
What do you call a pyramid with a triangle base?
A triangular pyramid is a pyramid having a triangular base. The tetrahedron is a triangular pyramid having congruent equilateral triangles for each of its faces. The regular tetrahedron is a special case of the triangular pyramid.
How many triangles are in a triangular pyramid?
A lower symmetry case of the triangular pyramid is C3v, which has an equilateral triangle base, and 3 identical isosceles triangle sides.
Why is a pyramid a triangle?
A triangle is formed by each pyramid’s side (every base edge and the apex). There are four triangular sides of a triangle-based pyramid. This means the pyramid’s three sides are the same size as each other, and if you rotate it, the pyramid looks the same.
Triangular Pyramid
A triangular pyramid is a pyramid having a triangular base. The tetrahedron is a triangular pyramid having congruent equilateral triangles for each of its faces.
Properties of Triangular Pyramid
A triangular pyramid has:
(i) A triangular pyramid has 4 vertices.
(ii) A triangular pyramid has 4 edge.
(iii) A triangular pyramid has 6 surface.
