NCERT Solutions for Class 7 Maths Chapter 5 Exercise 5.1 Lines and Angles in Hindi and English Medium for new academic year 2025-26. Get here the modified solutions of ex. 5.1 class 7th mathematics following the latest textbooks released for CBSE 2025-26 examinations.
NCERT Class 7 Maths Exercise 5.1 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 5 | Exercise: 5.1 |
| Topic: | Lines and Angles |
| Content Type: | Text, Images and Videos |
| Academic Year: | CBSE 2025-26 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 5 Exercise 5.1 Solution
All the solution are in PDF file format as well as videos format to learn in better way. Class 7 math NCERT exercise 5.1 contains questions based on complementary angles, supplementary angles, linear pair, opposite angles and similar other concepts of lines and angles.
Class 7 Maths Chapter 5 Exercise 5.1 Solution in Videos
Pairs of Angles
In geometry, we often come across pairs of angles. They have been given specific names.
Adjacent Angles: If two angles have:
(i) a common arm,
(ii) a common vertex and
(iii) their other arms lie on the opposite sides of the common arm, then the angles are called adjacent angles.
Class 7 Maths Exercise 5.1 Extra Questions
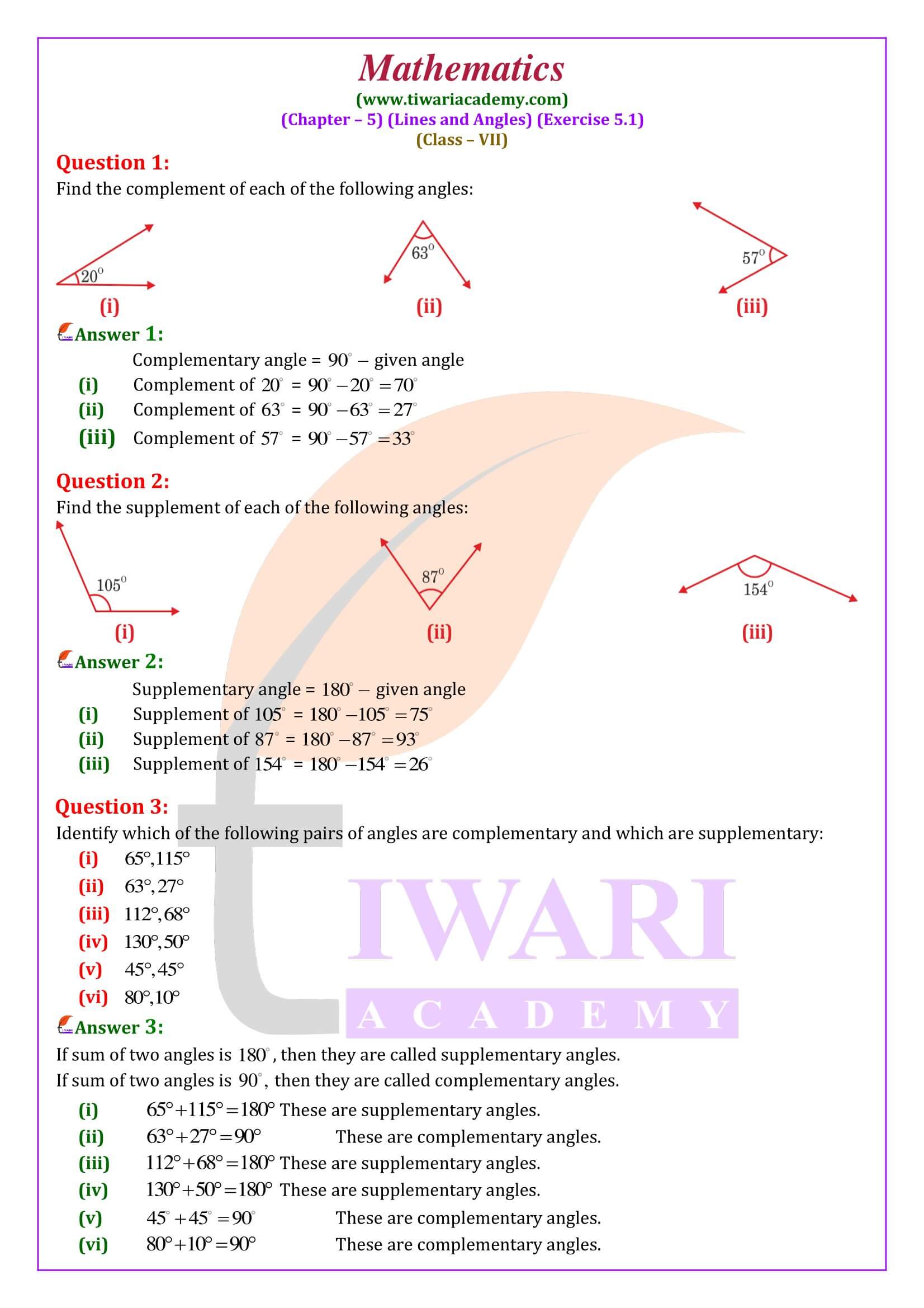
Find the complement of each of the following angles: (i) 60° (ii) 25°
(i) The given angle is 60°.
Let the measure of its complement be x°.
Then, x + 60 = 90
Or, x = (90 – 60) = 30°.
Hence, the complement of the given angle measures 30°.
(ii) The given angle is 25°.
Let the measure of its complement be x°.
Then, x + 25 = 90
Or, x = (90 – 25) = 65°.
Hence, the complement of given angle measures 65°.
Find the angles which is its own complement.
Let the measure of the required angle be x°.
Then, x + x = 90
Or, 2x = 90 Þ x = 45.
Hence, the required angle measures 45°.
Linear Pair of Angles
A linear pair is a pair of adjacent angles formed when two lines intersect. If a ray stands on a line, then the two adjacent angles formed these are called linear pair of angles.
Class 7 Maths Exercise 5.1 Important Questions
How many pairs of angles are there?
Two interesting varieties of angle pairs sum to 180°. These are linear pairs and supplementary angles. Linear pairs get their name because the sides not common to the two angles form a straight line. Linear pairs always share a common vertex and one common ray, line segment, or line.
Can two angles be supplementary if both of them are acute or obtuse?
Thus, the two acute angles cannot be supplementary angles. Thus, the two obtuses angles cannot be supplementary angles. Thus, two right angles are supplementary angles.
What is a requirement of complementary angles?
The measures of complementary angles must add up to 90°. The measures of complementary angles must add up to 180°.
Supplementary Angles
Two angles are said to be supplementary if the sum of their measures is 180°.
Thus, angle A and angle B are supplementary if angle A + angle B = 180°.
Example:
If angle A = 75° and angle B = 105° then angle A and angle B are supplementary, since angle A + angle B = 180°.
Complementary Angles
Two angles are said to be complementary if the sum of their measures is 90°.
Thus, angle A and angle B are complementary if angle A + angle B = 90°.
Example:
If angle A = 36° and angle B = 54° then angle A and angle B are complementary angles, since angle A + angle B = 90°.
Vertically Opposite Angles
Two angles are called a pair of vertically opposite angles if their arms form two pairs of opposite rays. Let two lines AB and CD intersect at a point O.
Then, two pairs of vertically opposite angles are formed:
(i) angle AOC and angle BOD
(ii) angle AOD and angle BOC.
Which questions of exercise 5.1 of 7th class Maths have the opportunity to come in the unit test?
Exercise 5.1 of 7th class Maths has 14 questions and one example (example 1). All sums of this exercise are good and logical. Students must solve all sums of this exercise. Questions 4, 6, 8, 9, 12 (ii), 13 (i), 14 of exercise 5.1 have more chances to come in the unit test compared to other questions of this exercise.
How many days are required to complete exercise 5.1 of class 7th Maths?
A maximum of 3-4 days (at least 1 hour per day) are required to complete exercise 5.1 of class 7th Maths because this exercise has 15 problems (14 questions and 1 example). This is not a fixed time. This time can vary also because no students can have the same speed, efficiency, etc.
What are the core motives of exercise 5.1 of grade 7th Maths?
The core motives of exercise 5.1 of grade 7th Maths are to teach students the following things:
1. Line
2. Line Segment
3. Point
4. Angle
5. Complementary Angles (When the sum of the measures of two angles is 90°, the angles are called complementary angles).
6. Supplementary Angles (When the sum of the measures of two angles is 180°, the angles are called supplementary angles).
7. Adjacent Angles
8. Linear Pair (A linear pair is a pair of adjacent angles whose non-common sides are opposite rays).
9. Vertically Opposite Angles
Is exercise 5.1 of 7th standard Maths simple?
Yes, exercise 5.1 of 7th standard Maths is very simple. Students enjoy doing this exercise. All questions of this exercise are good and logical. This is not a boring exercise. Also, short answer type questions (1 mark questions) can come from this exercise like fill in the blanks, true or false, MCQ, one word answer, etc