by Tiwari Academy
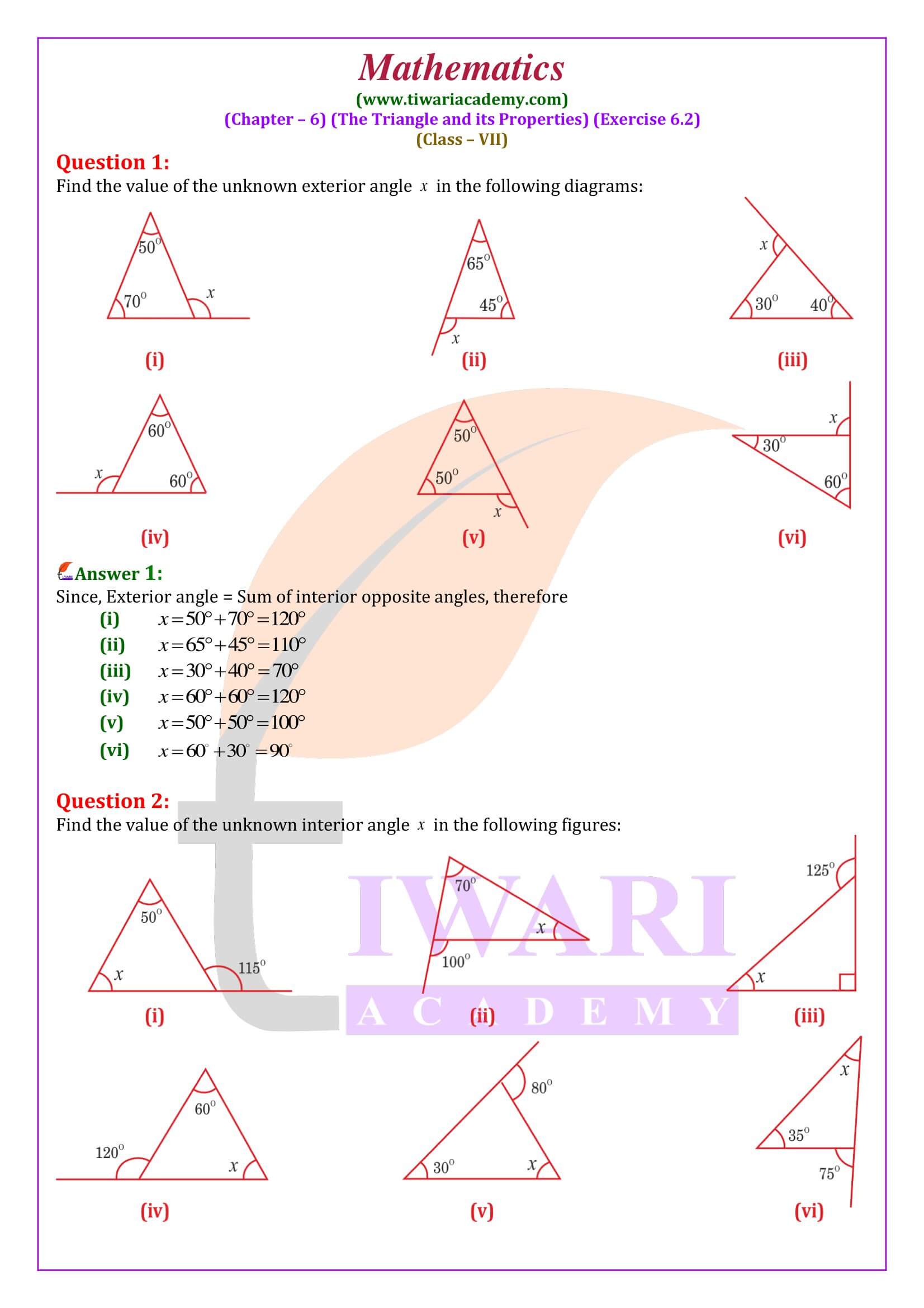
NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.2 Triangles and its Properties in English and Hindi Medium for CBSE 2024-25. Get the revised solutions of ex. 6.2 class 7th mathematics based on latest syllabus and new textbooks issued for academic year 2024-25.
NCERT Class 7 Maths Exercise 6.2 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 6 | Exercise: 6.2 |
| Chapter Name: | Triangles and its Properties |
| Content: | NCERT Book’s Solution |
| Session: | CBSE 2024-25 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 6 Exercise 6.2 Solution
All the contents and solutions are updated according to latest CBSE Syllabus 2024-25. Questions are taken from new NCERT books to make our contents up to date. Videos related to exercise 6.2 is also given, which is equally helpful for the children to understand the concepts.
Class 7 Maths Solution App in Hindi
Class 7 Maths Chapter 6 Exercise 6.2 Solution in Videos
Offline App for Class 7 Maths
Class 7 Maths Exercise 6.2 Extra Questions
In a triangle ABC, ∠A = 35° and ∠B = 65°, find the measure of ∠C.
We know that the sum of the angles of a triangle is 180°.
So, ∠A + ∠B + ∠C = 180°
∠ 35° + 65° + ∠C = 180°
Or, 100° + ∠C = 180°
Or, ∠C = 180° – 100° = 80°.
Hence, the measure of ∠C is 80°.
Two angles of a triangle are equal and the third angle measures 70°. Find the measure of each of the unknown angles.
Let the measure of each unknown angles be x°.
We know that the sum of the angles of a triangle is 180°.
So, x + x + 70 = 180
Or, 2x = (180 – 70)
Or, 2x = 110
Or, x = 55.
Hence, each unknown angles is 55°
Naming Triangles by Considering Their Angles
(i) Acute Triangle: A triangle each of whose angles measures less than 90° is called an acute triangle.
(ii) Right Triangle: A triangle one of whose angles measures 90° is called a right triangle.
(iii) Obtuse Triangle: A triangle one of whose angles measures more than 90° is called an obtuse triangle.
Class 7 Maths Exercise 6.2 Important Questions
The sum of the interior angles of a triangle is always 180 degrees. The exterior angle is the angle between any side of a shape, and a line extended from the next side. The sum of an exterior angle and its adjacent interior angle is also 180 degrees.
How many exterior angles does a triangle have?
Every triangle has 6 exterior angles, two at each vertex. Angles 1 through 6 are exterior angles. Notice that the “outside” angles that are “vertical” to the angles inside the triangle are NOT called exterior angles of a triangle.
Can you have a triangle with two right angles?
No, a triangle can never have 2 right angles. A triangle has exactly 3 sides and the sum of interior angles sum up to 180°. Thus, it is not possible to have a triangle with 2 right angles.
Some Results on Triangles
(i) Each angle of an equilateral triangle is 60°.
(ii) The angles opposite to equal sides of an isosceles triangle are equal.
(iii)A scalene triangle has no two angles equal.
Angle Sum Property of a Triangle
(i) a triangle cannot have more than one right angle
(ii) a triangle cannot have more than one obtuse angle
(iii) in a right triangle, the sum of the two acute angles is 90°.
Exterior and Interior Opposite Angles
Since an exterior angle of a triangle is equal to the sum of the interior opposite angles, it follows that an exterior angle is greater than each one of the interior opposite angles.
