by Tiwari Academy
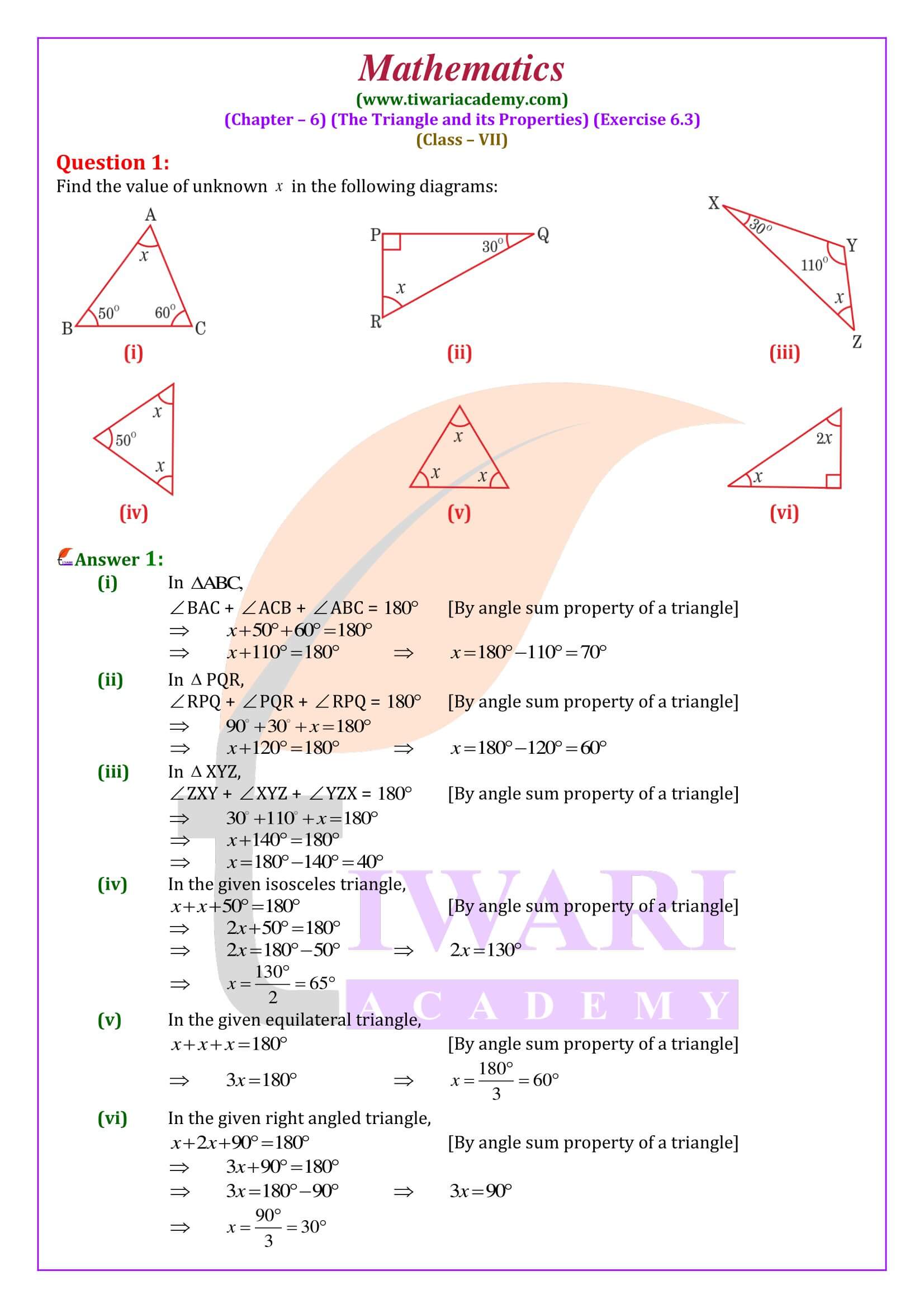
NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.3 Triangles and its Properties in Hindi and English Medium updated for CBSE Session 2024-25. All the questions given in ex. 6.3 of 7th mathematics are revised on the basis of new syllabus and latest textbooks issued for academic year 2024-25.
NCERT Class 7 Maths Exercise 6.3 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 6 | Exercise 6.3 |
| Topic Name: | Triangles and its Properties |
| Content: | NCERT Textbook Solution |
| Academic Year: | CBSE Session 2024-25 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 6 Exercise 6.3 Solution
Take help from videos solution, if someone is facing difficulty in understanding through PDF solution. In class 7 math NCERT exercise 6.3 most of the questions are based on vertically opposite angles, exterior angle, and angle sum properties of triangle. Questions are easy but should be done carefully.
Class 7 Maths Exercise 6.3 Extra Questions
Is it possible to draw a triangle whose sides have lengths 10.3 cm, 5.8 cm and 4.6 cm?
Clearly, we have: (10.3 + 5.8) > 4.6, (5.8 + 4.6) > 10.3, (10.3 + 4.6) > 5.8.
Thus, the sum of any two of these numbers is greater than the third side.
Hence, it is possible to draw a triangle whose sides are 10.3 cm, 5.8 cm and 4.6 cm.
Is it possible to draw a triangle whose sides are 5 cm, 7 cm and 12 cm?
Consider the numbers 5, 7 and 12.
Clearly, 5 + 7 = 12.
Thus, the sum of two of these numbers is not greater than the third number.
Hence, it is not possible to draw a triangle whose sides are 5 cm, 7 cm and 12cm.
Download Class 7 Maths Offline App
Class 7 Maths Chapter 6 Exercise 6.3 Solution in Videos
Class 7 Maths App in Hindi Medium
Triangle Inequality
In a Triangle ABC, let BC = a, CA = b and AB = c. An important property satisfied by all the sides of a triangle is given below, known as triangle inequality.
The sum of any two sides of a triangle is greater than the third side. In order to test the validity of the above statement, we perform the experiment given below.
Class 7 Maths Exercise 6.3 Important Questions
How do you find the inequality of a triangle?
The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side. Note: This rule must be satisfied for all 3 conditions of the sides.
When can we use the triangle inequality theorem?
Any side of a triangle must be shorter than the other two sides added together. If a side is equal to the other two sides it is not a triangle (just a straight line back and forth).
What is the 3-4-5 Triangle rule?
A 3-4-5 right triangle is a triangle whose side lengths are in the ratio of 3:4:5. In other words, a 3-4-5 triangle has the ratio of the sides in whole numbers called Pythagorean Triples.
Observations on sides of a triangle
(i) each value of (a + b – c) is positive;
(ii) each value of (b + c – a) is positive;
(iii)each value of (c + a – b) is positive.
Now, (a + b – c) > 0
Or, (a + b) > c, (b + c – a) > 0
Or, (b + c) > a, (c + a – b) > 0
Or, (c + a) > b.
So, the sum of any two sides of a triangle is greater than the third side.
Suppose three positive numbers are given. Then, a triangle with lengths of its sides given by these numbers is possible only when the sum of every pair of two of these numbers is greater than the third number.
Another Important Result The difference of any two sides of a triangle is less than the third side.
