NCERT Solutions for Class 7 Maths Chapter 8 Exercise 8.1 Rational Numbers in Hindi and English Medium for CBSE exams 2025-26. All the chapter 8 ex. 8.1 of 7th math is revised according to new syllabus and latest textbooks issued for academic session 2025-26.
NCERT Class 7 Maths Exercise 8.1 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 8 | Exercise: 8.1 |
| Topic Name: | Rational Numbers |
| Content: | Exercise and Extra Questions |
| Session: | CBSE 2025-26 |
| Medium: | English and Hindi Medium |
Class 7 Maths Chapter 8 Exercise 8.1 Solution
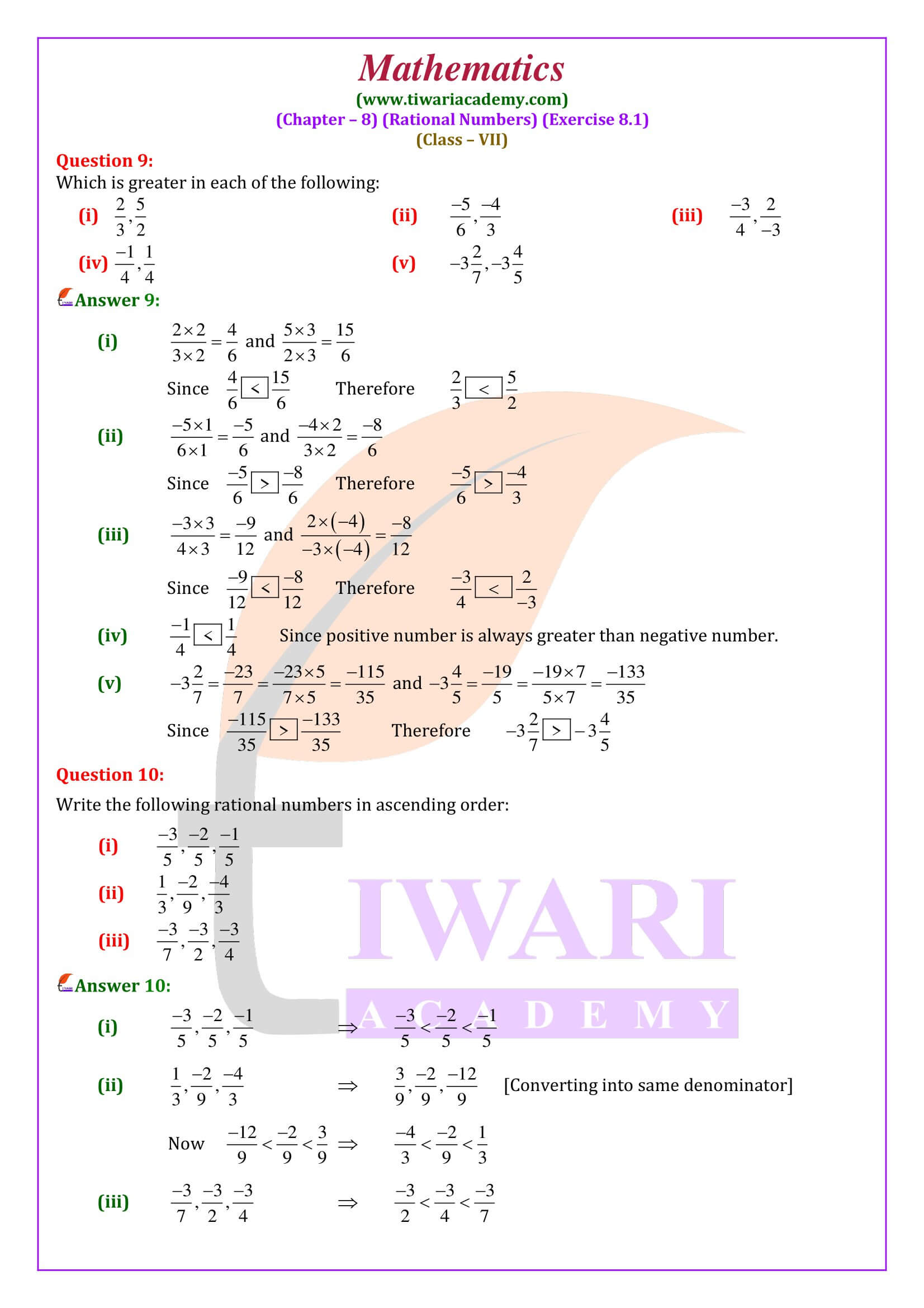
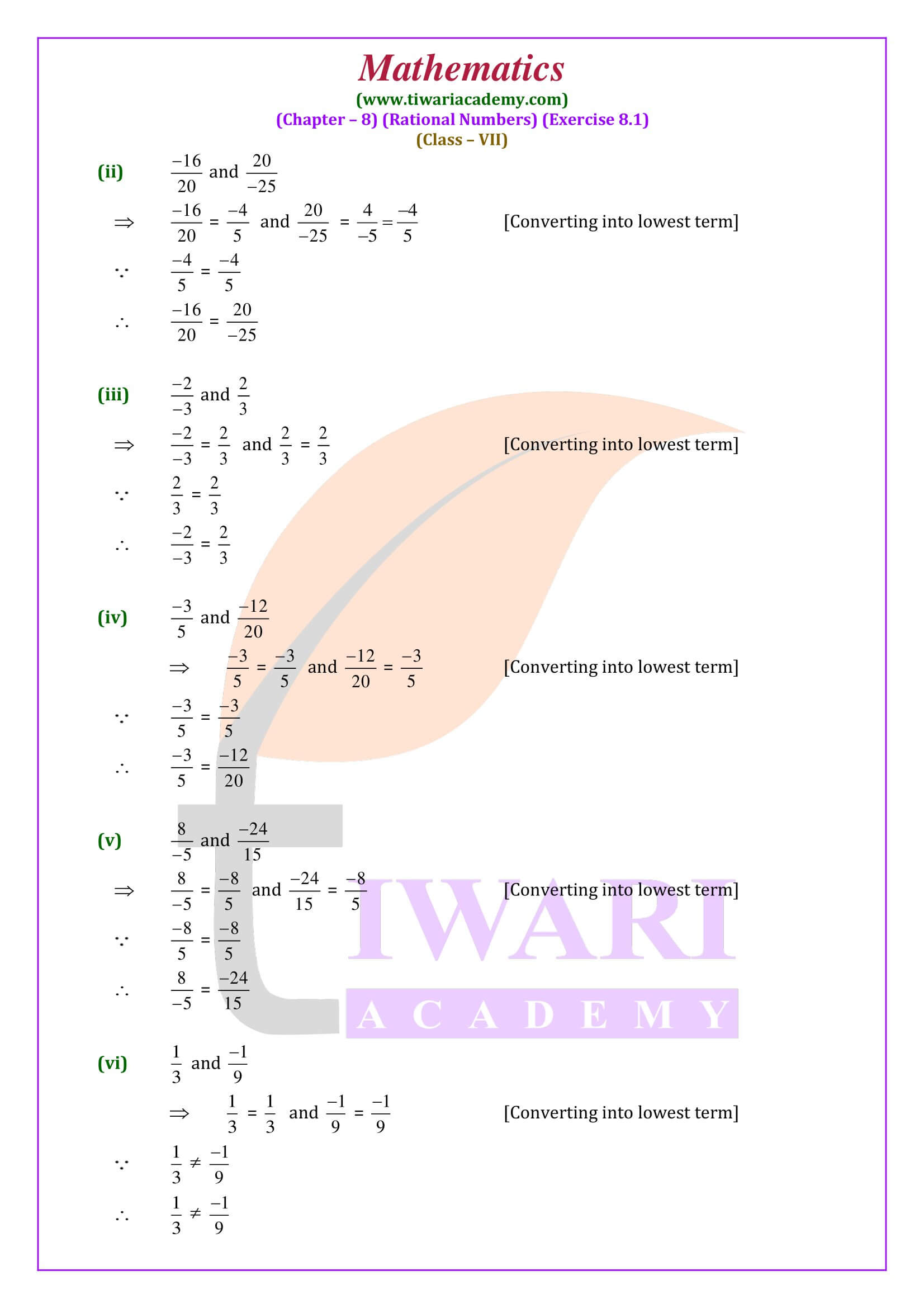
All the solutions and study material are updated according to latest NCERT Books 2025-26. In class 7 math exercise 8.1, we will learn to compare the rational numbers and plotting a rational number on number line. Finding more rational numbers between two given rational number is also important for next classes.
Class 7 Maths Chapter 8 Exercise 8.1 Solution in Videos
Natural Number
The counting number are called natural numbers. Thus, 1, 2, 3, 4, 5, 6, …, etc., are all natural numbers.
Whole Numbers
All natural numbers together with 0 (zero) are called whole numbers. Thus, 0, 1, 2, 3, 4, 5, 6, …., etc., are all whole numbers. Clearly, every natural number is a whole number but 0 is a whole number which is not a natural number.
Integers
All natural numbers, 0 and negatives of counting numbers are called integers.
Thus, …., – 5, – 4, – 3, -2, – 1, 0, 1, 2, 3, 4, 5, …, etc., are all integers.
1, 2, 3, 4, 5, 6, …., etc., are all positive integers.
– 1, – 2, – 3, – 4, – 5, – 6, …, etc., are all negative integers.
Zero is an integer which is neither positive nor negative.
Clearly, a positive integer is the same as a natural number
Fractions
The numbers of the form, where a and b are natural numbers, are called fractions.
Thus 2/3, 5/8, 3/11, 9/23, etc., are all fractions.
Rational Numbers
The numbers of the form p/q, where p and q are integers and q ≠ 0. are called rational numbers.
Examples of rational numbers
1. Each of the number 6/8, 9/12, 6/15, is a rational number.
2. Zero is a rational number, since we can write 0 = 0/1, which is the quotient of two integers with a nonzero denominator.
3. Every natural number is a rational number. We can write.
1 = 1/1, 2 = 2/1, 3 = 3/1, ………
In general, if n is a natural number, then we can write it as, which is a rational number.
4. Every integer is a rational number.
If m is an integer then we can write it as m/1, which is clearly a rational number. Thus, every integer is a rational number.
5. Every integer is a rational number. Let a/b be a fraction. Then, a and b are whole numbers and b ≠ 0. But, every whole number is an integer.
Thus, is the quotient of two integers such that b ≠ 0.
So, a/b is a rational number.
Hence, every fraction is a rational number.
Positive Rational Numbers
A rational number is said to be positive if its numerator and denominator are either both positive or both negative.
Example: Each of the number 5/7, 13/8, 17/9 etc.
Class 7 Maths Exercise 8.1 Important Questions
How are rational numbers used in everyday life?
Share something among friends: For example: if there are four friends and they want to divide a cake equally among themselves, then the quantity of cake that each friend will get will be one-fourth of the cake, that is a rational number 1/4.
Is 0 a rational number?
Yes, 0 is a rational number. Since we know, a rational number can be expressed as p/q, where p and q are integers and q is not equal to zero.
What are not irrational numbers?
A rational number is a number that can be express as the ratio of two integers. A number that cannot be expressed that way is irrational. For example, one third in decimal form is 0.33333333333333 (the threes go on forever).
Express each of the following numbers in standard form: (21/35)
(i) The given numbers is (21/35)
HCF of 21 and 35 is 7
So, we divide its numerator and denominator by 7
So, 21/35 = (21/7)/ (35/7) = 3/5
Negative Rational Numbers
A rational number is said to be negative if its numerator and denominator are such that one of them is a positive integer and the other is a negative integer.
Example: Each of the number -3/5, 5/-7, -9/11, is a negative rational number.
Three Important Properties of Rational Numbers
Theorem-1 of Rational Numbers:
If p/q is a rational number and m is a nonzero integer. Then = (p/q) x (m/m).
Thus, a rational number remains unchanged. if its numerator and denominator are multiplied by the same nonzero integer.
Theorem-2 of Rational Numbers:
If p/q is a rational number and m is a common divisor of p and q, then p/q = (p/m)/ (q/m).
Thus, on dividing the numerator and denominator of a rational number by a common divisor, it remains unchanged.
Equivalent Rational Numbers
On multiplying the numerator and denominator of a given rational number by the same nonzero number, we get a rational number equivalent to the given rational number.
Similarly, on dividing the numerator and denominator of a given rational number by a common divisor, we get a rational number equivalent to the given rational number.
Standard form of a Rational Number
A rational number p/q
METHOD: In order to express a given rational number in standard form, we first convert it into a rational number whose denominator is positive and then we divide its numerator and denominator by their HCF. is said to be in standard form, if q is positive, and p and q have no common divisor other than 1.
For any two rational a/b and c/d numbers and we have (a x d) = (b x c).
Theorem-3 of Rational Numbers
For any two rational numbers a/b and c/d we have (a x d) = (b x c).