by Tiwari Academy
NCERT Solutions for Class 7 Maths Chapter 9 Exercise 9.1 Perimeter and Area in Hindi and English Medium updated for 2024-25. The questions given in the chapter end exercised are revised according to new syllabus and current NCERT textbook published for academic session 2024-25.
NCERT Class 7 Maths Exercise 9.1 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 9 | Exercise: 9.1 |
| Chapter Name: | Perimeter and Area |
| Content Type: | PDF and Video Solutions |
| Academic Session: | CBSE 2024-25 |
| Medium: | English and Hindi Medium |
Class 7 Maths Chapter 9 Exercise 9.1 Solution
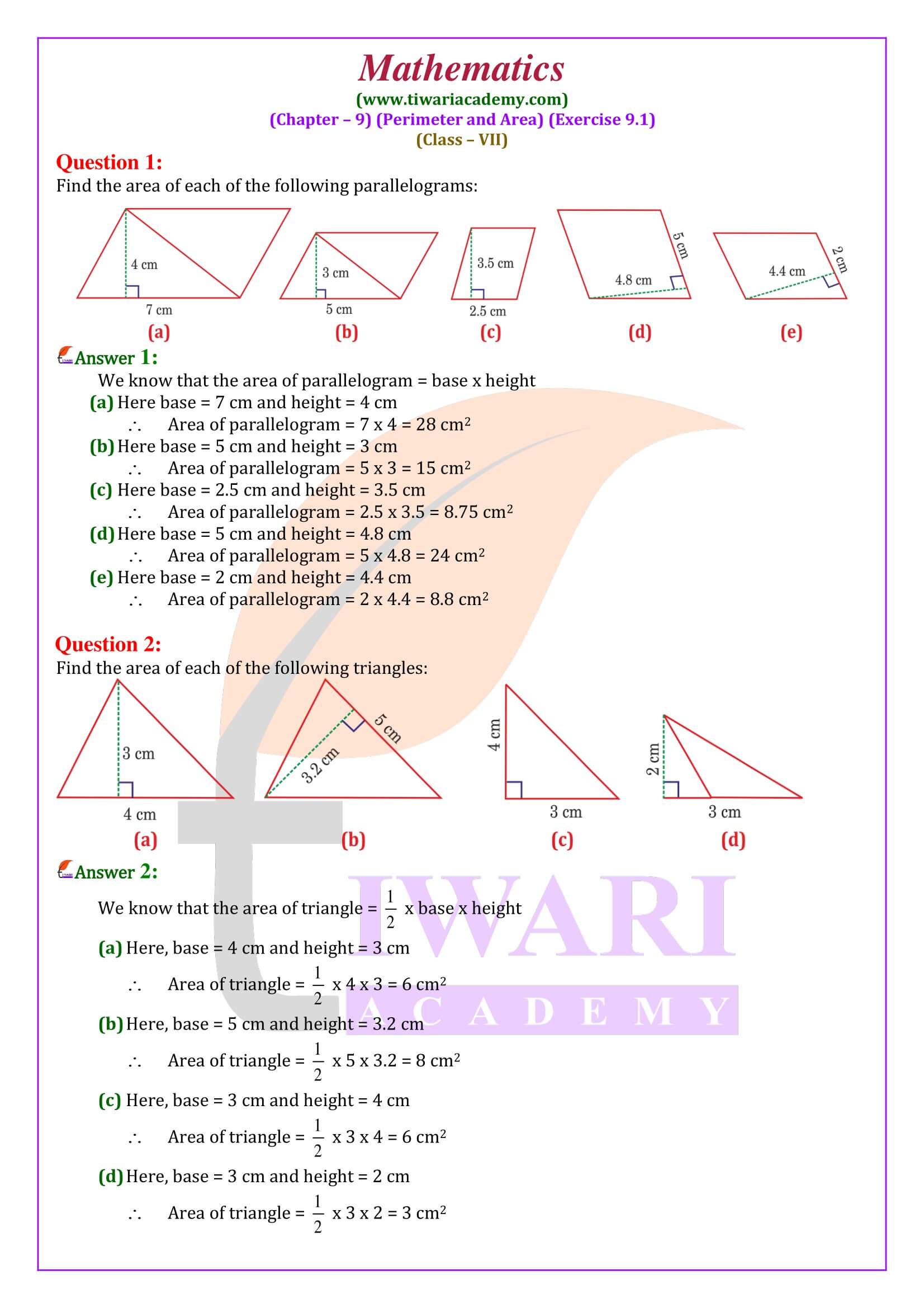
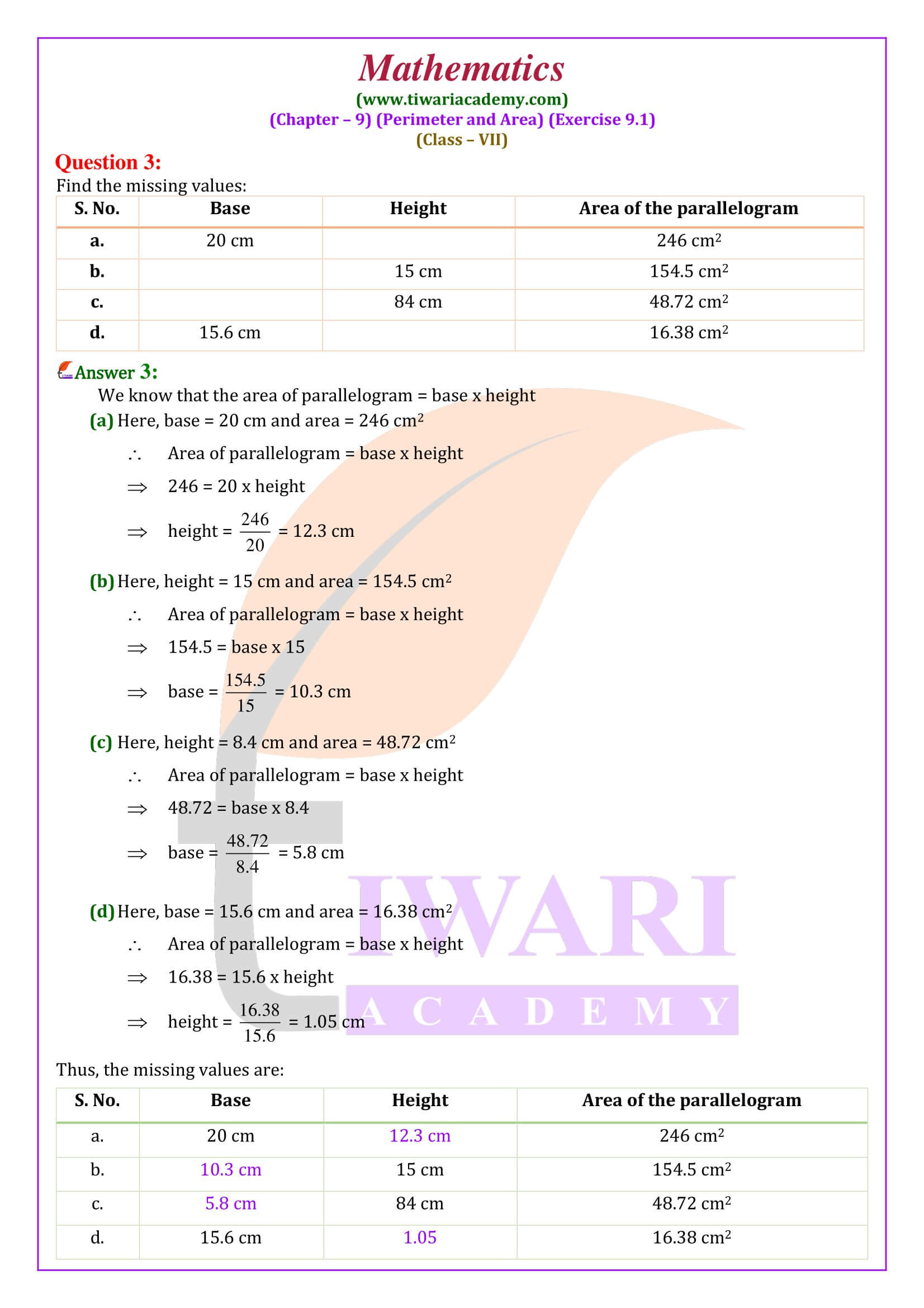
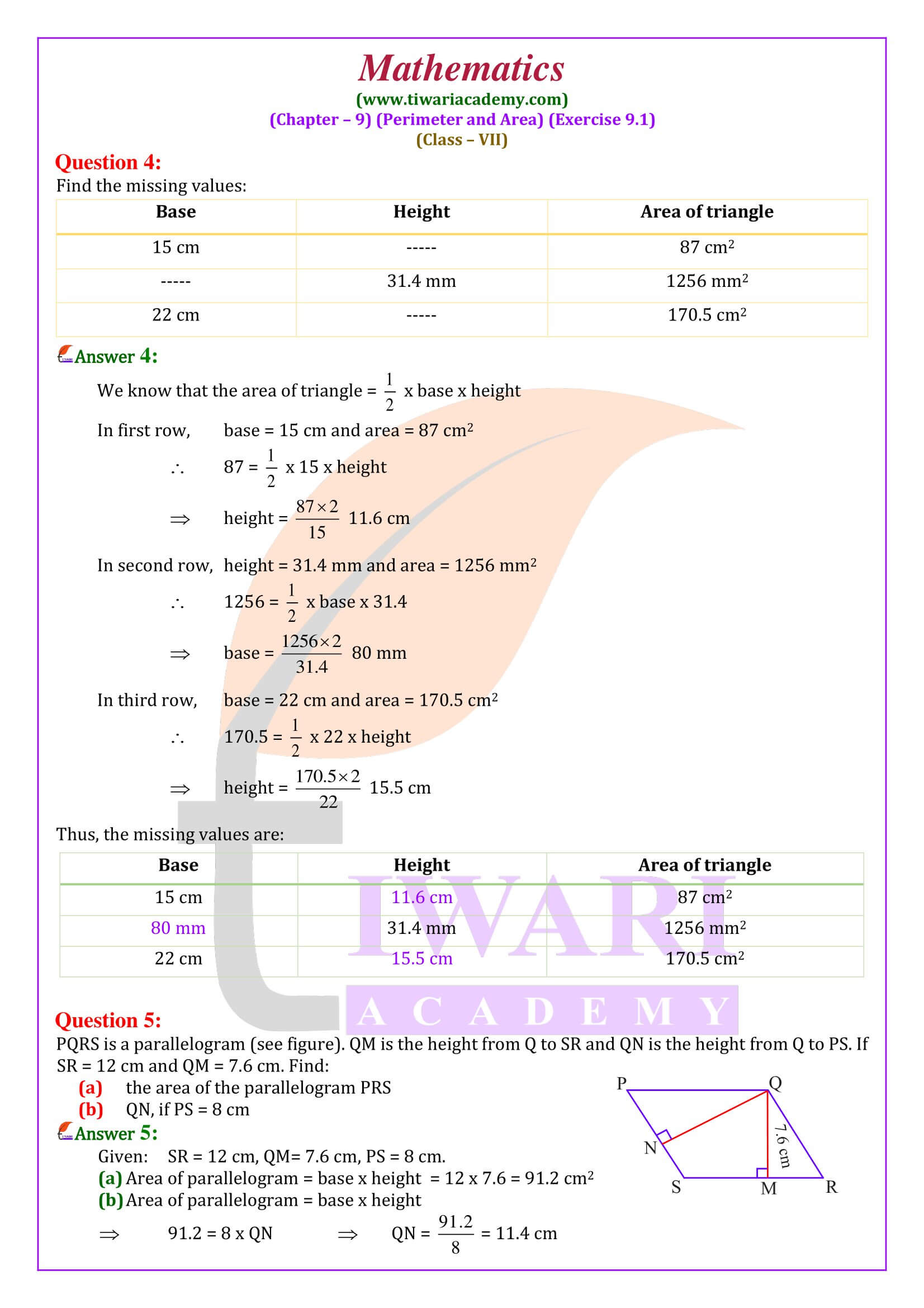
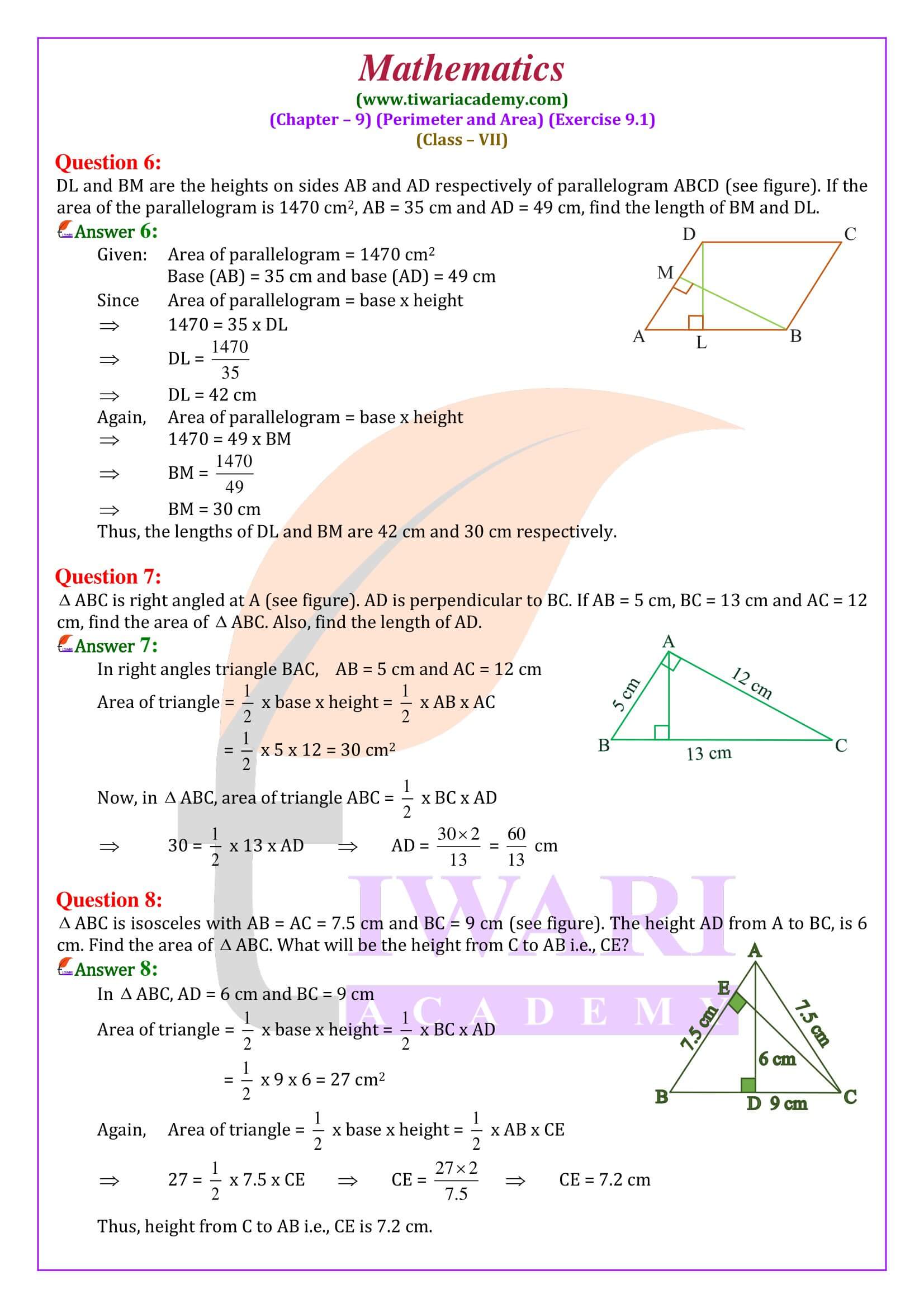
Videos solution and PDF solution both are given in Hindi and English Medium. Practice here the questions based on areas of triangle and parallelograms. There are total 8 questions in NCERT exercise 9.1 of class 7 math, and most of the questions are easy to solve and understand.
Class 7 Maths Exercise 9.1 Extra Questions
A rectangular park is 45 m long and 30 m wide, a path 2.5 m wide is constructed outside the park. Find the area of the path and the cost of constructing it at Rs. 125 per m².
A rectangular park is 45 m long and 30 m wide, a path 2.5 m wide is constructed outside the park. Find the area of the path and the cost of constructing it at Rs. 125 per m².
Let ABCD be the given park surrounded externally by a 2.5 m wide path.
Let EFGH be the external boundary of the path. Length of park = 45 m and breadth of park = 30 m.
Area of the park ABCD = (45 x 30) m2 = 1350 m².
Width of the path = 2.5 m.
External length EF = (45 + 2 x 2.5) m = 50 m.
External breadth FG = (30 + 2 x 2.5) m = 35 m.
Area of rect. EFGH = (50 x 35) m2 = 1750 m².
Area of the path = (area of rect. EFGH) – (area of rect. ABCD) = (1750 – 1350) = 400 m².
So, cost of constructing the path = Rs. (400 x 125) = Rs. 50000.
A rectangular lawn is 60m by 40 m and has two roads, each 5 m wide running in the middle of it, one parallel to its length and the other parallel to the breadth. Find the cost of constructing the roads at Rs. 80 per m².
Let ABCD and EFGH be the two roads.
Area of these two roads = (area ABCD) + (area EFGH) – (area PQRS)
= {(60 x 5) + (40 x 5) – (5 x 5)} m²
= (300 + 200 – 25 m = 475 m².
So, cost of constructing the roads = Rs. (475 x 80) = Rs. 38000.
Class 7 Maths Offline App
Class 7 Maths Exercise 9.1 Important Questions
Can perimeter be greater than area?
That means, any square with a side length less than 4, will have a larger perimeter than area. Technically: no, because area and perimeter are measured with different units, and so they can’t be just compared. Numerically: yes, it just depends on your units.
A square lawn has a 2 m wide path surrounding it. If the area of the path is 136 m², find the area of the lawn.
Let ABCD be the lawn and let EFGH be the outer boundary of the path around the lawn.
Let AB = x metres.
Then, EF = (x + 2 + 2) m = (x + 4) m.
Area of the square ABCD = AB2 = (x²) m².
Area of the square EFGH = EF² = (x + 4)² m².
Area of the path = (area of sq. EFGH) – (area of sq. ABCD)
= {(x + 4)² – x²} m²
= (16 + 8x) m².
16 + 8x = 136 m²
Or, 8x = 120
Or, x = 15 m area of the lawn (15 x 15) m².
So, area of the lawn = 225 m².
Are two squares always similar?
Now, all squares are always similar. Their size may not be equal but their ratios of corresponding parts will always be equal. As, the ratio of their corresponding sides is equal hence, the two squares are similar.
Class 7 Maths Chapter 9 Exercise 9.1 Solution in Videos
Class 7 Maths Offline App in Hindi
Area Between Two Rectangles
In order to find the area between rectangles subtract area of smaller rectangle from the area of larger rectangle.
