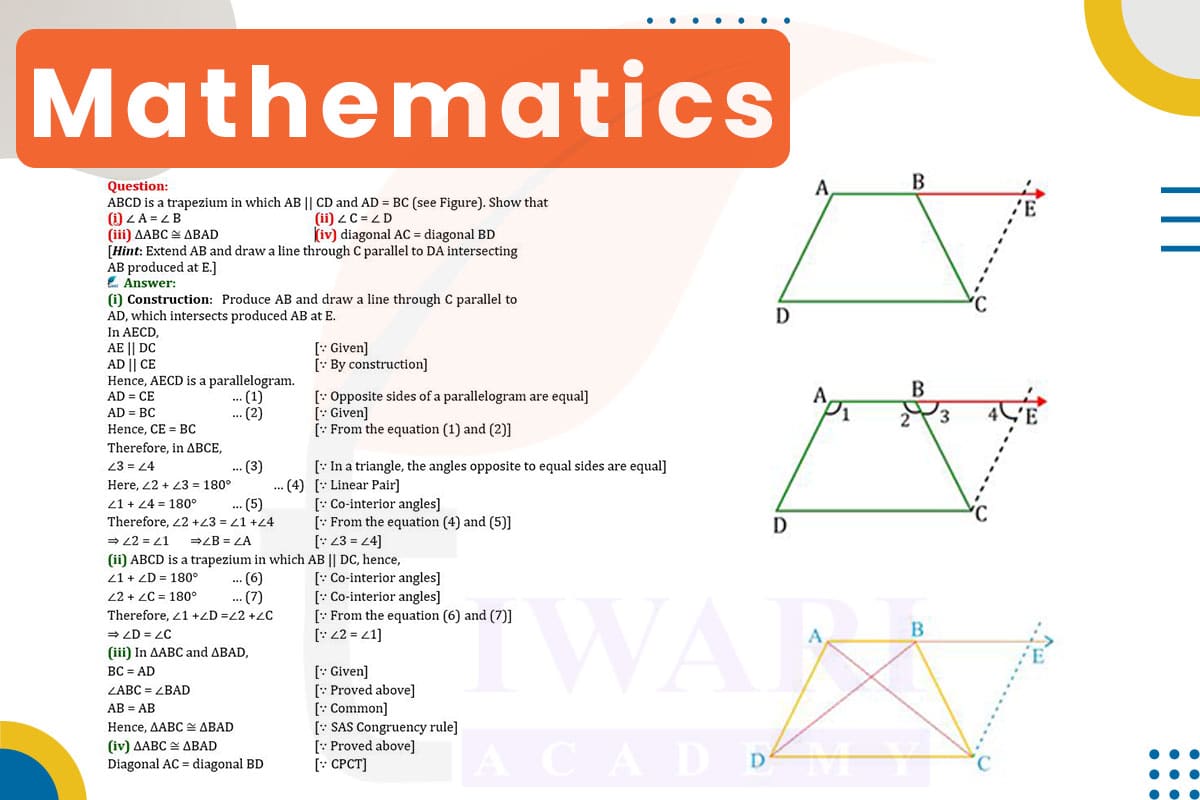
In trapezium ABCD, where AB is parallel to CD and AD equals BC:
(i) ∠A = ∠B: Since AB is parallel to CD, and AD is a transversal, ∠DAB (exterior angle) equals ∠ABC (interior opposite angle) due to alternate interior angles in parallel lines.
(ii) ∠C = ∠D: Similarly, since AB is parallel to CD and BC is a transversal, ∠BCD equals ∠BAD due to alternate interior angles.
(iii) Δ ABC ≅ Δ BAD: Triangles ABC and BAD have AD = BC (given), ∠A = ∠B, and AB common. By SAS (Side-Angle-Side) congruence, Δ ABC ≅ Δ BAD.
(iv) Diagonal AC = Diagonal BD: From the congruence of Δ ABC and Δ BAD, corresponding parts are equal, so diagonal AC equals diagonal BD.
Let’s discuss in detail
Introduction to Trapezium ABCD
In the trapezium ABCD, where AB is parallel to CD and the non-parallel sides AD and BC are equal, a unique geometric scenario is presented. A trapezium, or trapezoid, is a four-sided figure with at least one pair of parallel sides. In this case, the additional condition of two non-parallel sides being equal introduces special properties and relationships between the angles and sides of the trapezium. Understanding these relationships is key to uncovering the congruences and equalities within the trapezium, demonstrating the elegance and interconnectedness of geometric principles.
Angle Relationships in Trapezium ABCD
The first property to note is that ∠A equals ∠B. This equality arises because AB is parallel to CD, making AD a transversal. In such a configuration, alternate interior angles are equal. Therefore, ∠DAB (an exterior angle of ΔBAD) is equal to ∠ABC (an interior opposite angle of ΔABC). This relationship is a direct consequence of the parallelism of AB and CD and is a fundamental aspect of the geometry of parallel lines intersected by a transversal.
Equality of Opposite Angles
Similarly, the equality of ∠C and ∠D can be established using the same principle of parallel lines and a transversal. Since AB is parallel to CD and BC acts as a transversal, the alternate interior angles ∠BCD and ∠BAD are equal. This equality of angles is another critical aspect of the geometry of trapezium ABCD, further indicating a symmetry in the figure that is not immediately apparent but is revealed through the analysis of angles.
Congruence of Triangles ABC and BAD
The congruence of triangles ABC and BAD is established through the Side-Angle-Side (SAS) congruence criterion. We have two pairs of equal sides: AD equals BC (given) and AB is common to both triangles. Additionally, we have established that ∠A equals ∠B. These conditions satisfy the SAS criterion, proving that Δ ABC is congruent to Δ BAD. This congruence is significant as it indicates a high degree of symmetry in trapezium ABCD, despite its non-regular shape.
Equality of Diagonals AC and BD
From the congruence of triangles ABC and BAD, it follows that corresponding parts of congruent triangles are equal. Therefore, the diagonals AC and BD, which are corresponding parts of these triangles, must be equal in length. This equality of diagonals is a remarkable property for a trapezium and is a direct result of the specific conditions in trapezium ABCD – parallel sides AB and CD and equal non-parallel sides AD and BC.
Symmetry in Trapezium ABCD
In conclusion, trapezium ABCD, with its parallel sides AB and CD and equal sides AD and BC, exhibits a surprising level of symmetry and congruence. The equal angles (∠A = ∠B and ∠C = ∠D) and the congruence of triangles ABC and BAD, leading to equal diagonals AC and BD, reveal a harmonious geometric structure. This example illustrates the depth of geometric principles, showing how specific conditions in a seemingly simple shape can lead to unexpected symmetries and congruences, highlighting the beauty and complexity of geometry.
Discuss this question in detail or visit to Class 9 Maths Chapter 8 for all questions.
Questions of 9th Maths Exercise 8.1 in Detail


