In a parallelogram ABCD, E and F are the mid-points of sides AB and CD

Updated on November 25, 2023
by Tiwari Academy

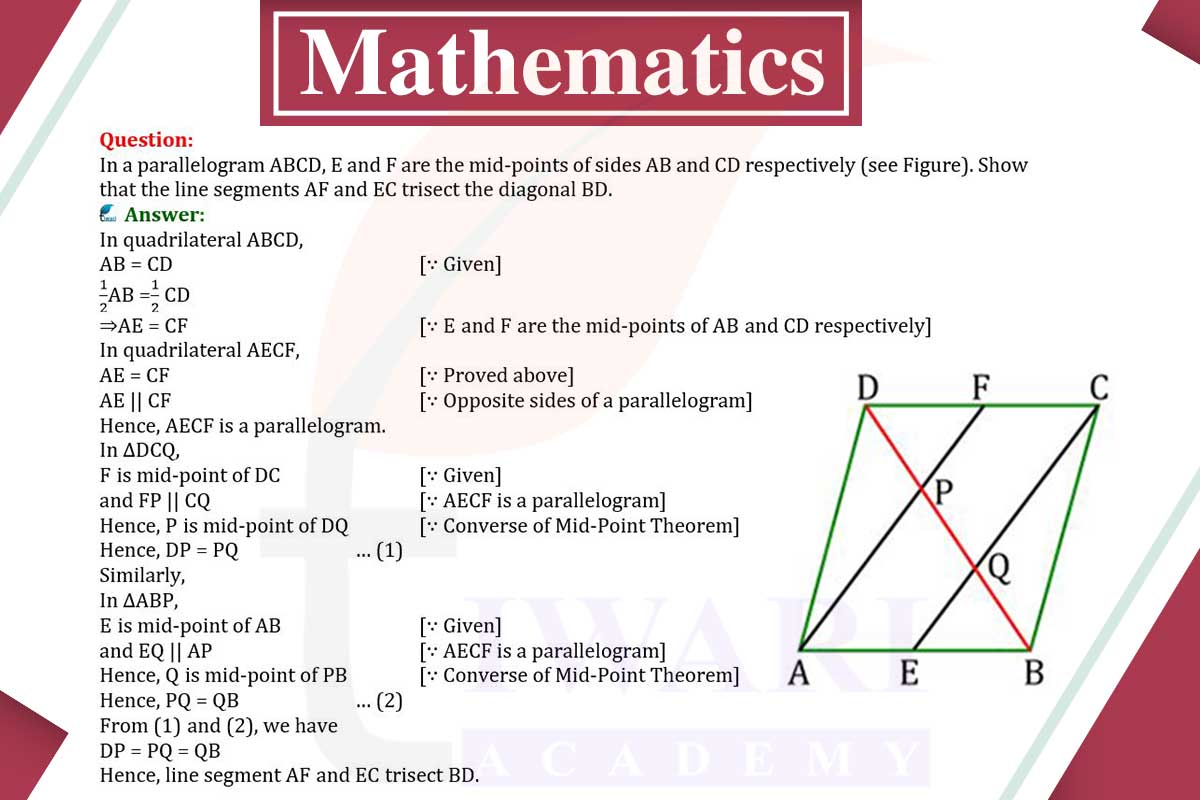
In parallelogram ABCD, with E and F as mid-points of AB and CD respectively:
Triangles AED and BFC are Congruent: In parallelogram ABCD, AB = CD and AD = BC. Since E and F are midpoints, AE = EB and CF = FD. By SAS (Side-Angle-Side) criterion, ΔAED ≅ ΔBFC.
AF and EC are Equal: From the congruence of ΔAED and ΔBFC, AF = EC.
AF and EC Trisect BD: Since AF = EC and E, F are midpoints, AF, FE, and EC are equal. Thus, AF, FE, and EC divide BD into three equal parts, trisecting it.

In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect BD.

Let’s discuss in detail

Parallelogram ABCD and Midpoints

In parallelogram ABCD, points E and F are defined as the midpoints of sides AB and CD, respectively. A parallelogram is a geometric figure with opposite sides that are parallel and equal in length. The introduction of midpoints on the sides of a parallelogram creates an opportunity to explore the relationships between various line segments within the figure. Specifically, the line segments AF and EC, when drawn from these midpoints to the opposite vertices, present a unique case for examination. The goal is to demonstrate how these segments interact with the diagonal BD of the parallelogram.

Congruence of Triangles AED and BFC

To understand the relationship between the line segments AF and EC and the diagonal BD, it’s essential to first establish the congruence of triangles AED and BFC. In parallelogram ABCD, sides AB and CD are equal, as are sides AD and BC. Since E and F are midpoints, AE equals EB, and CF equals FD. By the Side-Angle-Side (SAS) criterion of congruence, triangles AED and BFC are congruent, as they have two sides and the included angle equal.

Equality of Line Segments AF and EC

From the congruence of triangles AED and BFC, it follows that corresponding parts of congruent triangles are equal. Therefore, line segment AF in triangle AED is equal in length to line segment EC in triangle BFC. This equality is significant as it establishes a symmetrical relationship between these line segments, which is a key step in proving that they trisect the diagonal BD.

Trisecting the Diagonal BD
The line segments AF and EC, being equal in length, suggest a division of the diagonal BD into segments of equal length. Since E and F are midpoints of AB and CD, respectively, line segment FE is also a part of the diagonal BD. The equality of AF and EC, along with the positioning of E and F, implies that the segments AF, FE, and EC are all equal in length. This equality of segments indicates that the diagonal BD is trisected by these line segments.

Implications of Trisection in Parallelogram ABCD

The trisection of diagonal BD by the line segments AF and EC has significant geometric implications. It demonstrates a harmonious division of the parallelogram’s diagonal, reflecting the symmetry and balance inherent in the shape. This trisection is not just a feature of this particular parallelogram but is a general property applicable to any parallelogram with similar constructions. It showcases the elegance and consistency of geometric principles, particularly in figures like parallelograms where parallelism and symmetry play crucial roles.

Geometric Harmony in Parallelogram ABCD

In conclusion, the parallelogram ABCD, with midpoints E and F on its sides, exhibits a fascinating geometric property where the line segments AF and EC trisect the diagonal BD. This trisection is a direct result of the congruence of triangles AED and BFC and the equality of the line segments AF and EC. This example highlights the beauty and precision of geometry, where simple constructions can lead to profound and elegant results, demonstrating the interconnectedness and harmony of geometric elements within a shape.

Discuss this question in detail or visit to Class 9 Maths Chapter 8 for all questions.
Questions of 9th Maths Exercise 8.2 in Detail

ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that: (i) SR || AC and SR = 1/2AC (ii) PQ = SR (iii) PQRS is a parallelogram.

ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.

ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F. Show that F is the mid-point of BC.

In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) MD⊥AC (iii) CM = MA = 1/2AB.