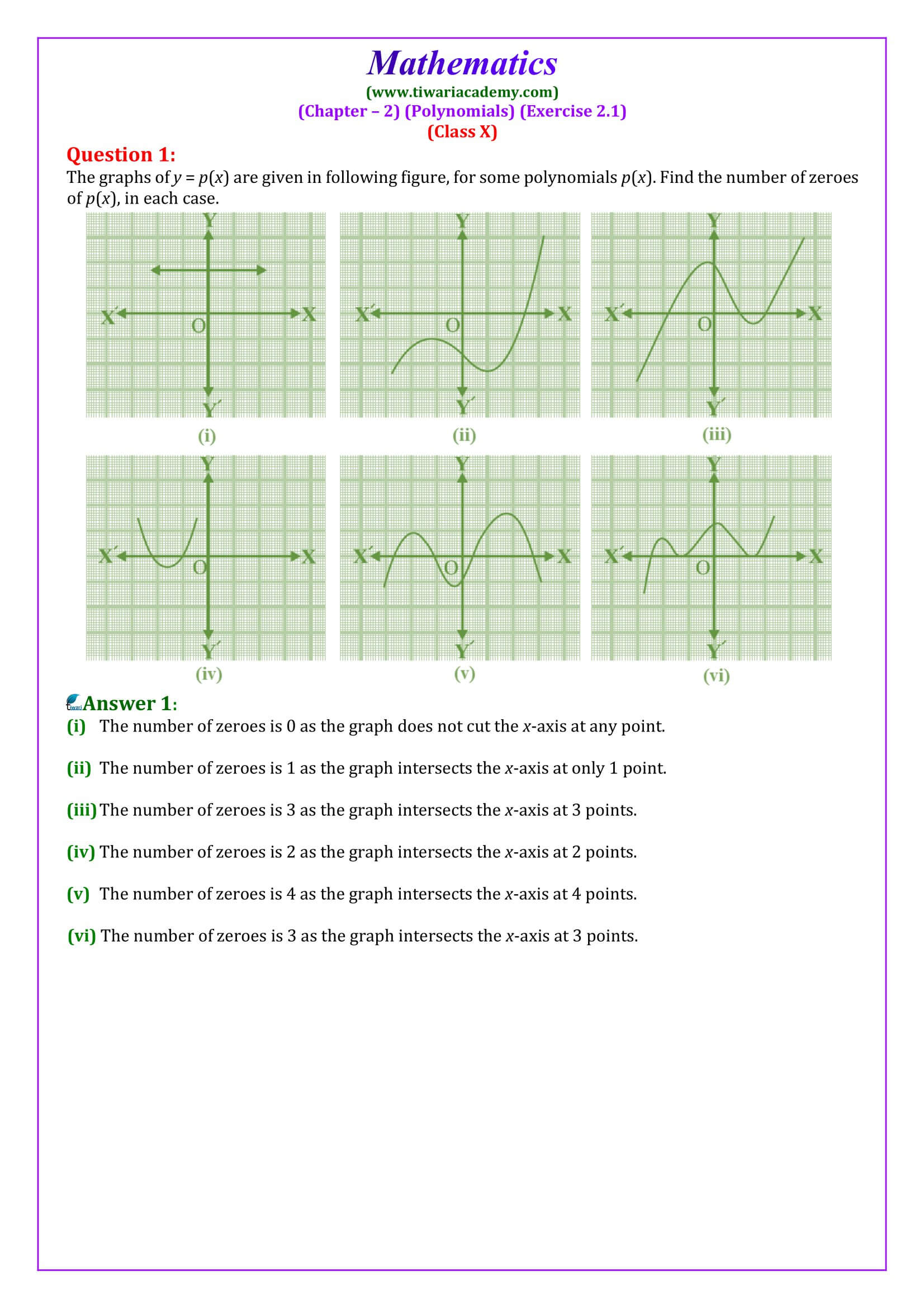
NCERT Solutions for Class 10 Maths Chapter 2 Exercise 2.1 Polynomials Updated for New Session 2025-26 in Hindi and English Medium. Get the modified solutions of ex. 2.1 class 10th mathematics based on current syllabus and revised NCERT textbooks issued for academic year 2025-26.
NCERT Exercise 2.1 Solutions for Class 10 Maths
Class 10 Maths Chapter 2 Exercise 2.1 Board Questions Solutions
1. Shown below is an expression (x² – 2√3x – 9)/(x + √3), x ≠ -√3. At how many points does the graph of the above expression intersect the X-axis?
See Solution2 points
Explanation: The expression equals 0 when the numerator equals 0: x² – 2√3x – 9 = 0
Using the quadratic formula:
x = (2√3 ± √(12 + 36))/2
x = (2√3 ± √48)/2
x = (2√3 ± 4√3)/2
x = √3 ± 2√3
Therefore, x = 3√3 or x = -√3
However, x = -√3 is not in the domain. Therefore, there is only one x-value where the expression equals 0: x = 3√3.
The graph intersects the x-axis at only one point where x = 3√3.
Let’s redo the calculation: x² – 2√3x – 9 = 0 Using the quadratic formula:
x = (2√3 ± √(12 + 36))/2
x = (2√3 ± √48)/2
x = (2√3 ± 4√3)/2
x = √3 ± 2√3
This gives x = 3√3 or x = -√3
Since x ≠ -√3 (domain restriction), the expression equals 0 only at x = 3√3.
Therefore, the graph intersects the X-axis at exactly 1 point.
2. When a polynomial is divided by (2x – 1), the quotient is (3x – 2) and the remainder is (x – 3). Find the polynomial.
See Solution6x² – 7x + 2
Explanation: When a polynomial p(x) is divided by (2x – 1), we have: p(x) = (2x – 1)(3x – 2) + (x – 3)
Expanding: p(x) = 6x² – 4x – 3x + 2 + x – 3 p(x) = 6x² – 6x – 1
Wait, let us recalculate:
p(x) = (2x – 1)(3x – 2) + (x – 3)
p(x) = 6x² – 4x – 3x + 2 + x – 3
p(x) = 6x² – 6x – 1
Let us try once more:
p(x) = (2x – 1)(3x – 2) + (x – 3)
p(x) = 6x² – 3x – 2x + 1 + x – 3
p(x) = 6x² – 4x – 2
Let us be more careful: p(x) = (2x – 1)(3x – 2) + (x – 3)
= 6x² – 4x – 3x + 2 + x – 3
= 6x² – 6x – 1
Let’s expand once more step by step:
(2x – 1)(3x – 2)
= 6x² – 4x – 3x + 2
= 6x² – 7x + 2
Therefore: p(x) = (2x – 1)(3x – 2) + (x – 3) = 6x² – 7x + 2 + x – 3 = 6x² – 6x – 1
Let’s approach this differently: If p(x) = (2x – 1)q(x) + r(x) where q(x) = 3x – 2 and r(x) = x – 3
Then p(x) = (2x – 1)(3x – 2) + (x – 3)
Expanding: p(x) = 6x² – 4x – 3x + 2 + x – 3 = 6x² – 6x – 1
3. Let f(x) = ax² + bx + 325 is a polynomial, where a and b are real numbers. The zeroes of f(x) are distinct prime numbers. Find the (i) zeroes of f(x). (ii) values of a and b.
See Solutionf(x) = 5x² − 90x + 325
Explanation: Let the polynomial be: f(x) = ax² + bx + 325
We are given:
– Zeroes are distinct prime numbers: a, b ∈ ℝ
– Constant term = 325
Step 1: Use the fact about zeroes and constant term
For a quadratic polynomial of the form: f(x) = ax² + bx + c
The product of the zeroes = c / a = 325 / a
Let the zeroes be p and q, both distinct prime numbers.
So, pq = 325/a
⇒ 325 = a·p·q
Now we factor 325: 325 = 5 × 5 × 13
So, the possible pair of distinct prime factors = 5 and 13
Let the zeroes be p = 5, q = 13
Then: pq = 5 × 13 = 65
So, a·65 = 325
⇒ a = 325 / 65 = 5
Step 2: Find b using sum of zeroes
Sum of zeroes = −b / a
p + q = 5 + 13 = 18
So, 18 = −b / a
⇒ −b = 18a = 18 × 5 = 90
⇒ b = −90
Final Answers:
(i) Zeroes of f(x) = 5 and 13
(ii) Values: a = 5 and b = −90
4. g(x) = px² + qx + 152 is a polynomial, where p and q are real numbers. The zeroes of g(x) are distinct prime numbers. Find the (i) zeroes of g(x). (ii) values of p and q.
See Solution(i) The zeroes are 8 and 19 (ii) p = 1, q = -27
Explanation: If r and s are the prime zeroes of g(x), then: g(x) = p(x – r)(x – s) = p(x² – (r+s)x + rs)
Since the constant term is 152, we have: p × rs = 152
The prime factorization of 152 is 2³ × 19 = 8 × 19.
But 8 = 2³ is not a prime number.
Actually, I think there’s no valid solution for this problem since there are no two distinct prime numbers whose product is 152.
Let me reconsider. The factor 8 is not prime (it’s 2³), so there are no two distinct prime numbers whose product is 152.
For Exercise 2.1 in class 10 Maths Chapter 2 (Polynomials), to prepare effectively for exams, you should first focus on understanding the graphical representation of polynomial zeroes. This exercise involves interpreting graphs to identify the number of zeroes of a given polynomial. Spend time practicing how to read graphs and understand the relationship between the x-axis and the zeroes of different types of polynomials. Focus on identifying how linear, quadratic and cubic polynomials behave graphically, as this will be key to answering these questions. Review past problems and ensure you can quickly determine zeroes based on visual cues.
Work on speed and accuracy. Time yourself while solving multiple problems of this type, ensuring that you can correctly identify zeroes in a given time frame. This exercise is likely to appear in exams where quick graphical interpretation is needed. Practice sketching simple polynomial graphs yourself to build intuition and ensure you know how changes in the coefficients of polynomials affect the graph’s shape and the location of zeroes.
Class 10 Maths Exercise 2.1 Solutions in Hindi and English Medium
| Class: 10 | Mathematics |
| Chapter 2: | Exercise 2.1 |
| Content: | Textbook Exercises Solutions |
| Mode of Content: | Images, Text, PDF and Videos |
| Academic Session: | Year 2025-26 |
| Medium: | English and Hindi Medium |
NCERT Solutions for class 10 Maths Chapter 2 Exercise 2.1
Class 10 Maths Ex. 2.1 Polynomials – Bahupad Hindi Medium and English Medium download in PDF format or View in Video Format free for new academic session 2025-26. All the contents are free to use for all users without any long or password. UP Board students can take benefits of these solutions as they are using NCERT Books for their course. Explanation of all the questions are in Hindi and English medium with examples. Videos related to 10th Maths Ex. 2.1 solutions are also given below. Offline Solutions Apps are updated according to new CBSE Syllabus 2025-2026 for Gujrat Board, CBSE with Uttarakhand & UP Board students studying NCERT Books. Download Exercise 2.1 in PDF format solutions or use it online without download. Enjoy all the contents free of cost and use without any restrictions as all the contents on Tiwari Academy is free to use.
NCERT 10th Maths Chapter 2 Exercise 2.1 Solutions
NCERT Exercises Solutions for class 10 Maths Chapter 2 Ex 2.1 Polynomials in Hindi and English medium to use it online or download in PDF. If you find any difficulty or error in these solutions, please inform us. We are here to help you in education without any charges.
Important Questions of 10th Maths Exercise 2.1
What is meant by degree of a polynomial?
If p(x) is a polynomial in x, the highest power of x in p(x) is called the degree of the polynomial p(x).
Which type of polynomial is called a linear polynomial?
A polynomial of degree 1 is called a linear polynomial.
What is a quadratic polynomial?
A polynomial of degree 2 is called a quadratic polynomial. The name QUADRATIC has been derived from the word QUADRATE, which means SQUARE.
Name the polynomial with degree three?
A polynomial of degree 3 is called a cubic polynomial.
Class 10 Maths Exercise 2.1 Solution in Hindi Medium Video
Important Terms related to Polynomials
1. Polynomial: If x is a variable, n is a natural number and a0, a1, a2, a3, ………. an are real numbers, then p(x) = an x^n + a^n-1. X^x-1 + ……… + a1 x + a0, (an ≠ 0) is called a polynomial in x.
2. Polynomials of degree 1, 2 and 3 are called linear, quadratic and cubic polynomials respectively.
3. A quadratic polynomial is an algebraic expression of the form ax² + bx + c, where a, b, c are real numbers with a ≠ 0.
4. Zeroes of a polynomial p(x) are precisely the x – coordinates of the points where the graph of y = p(x) intersects the x–axis, i.e., x = a is a zero of polynomial p(x) if p(a) = 0.
5. Division Algorithm states that given any polynomials p(x) and g(x), there exist polynomial q(x) and r(x) such that: p(x) = g(x). q(x) + r(x) ; g(x) ≠ 0, [where either r(x) = 0 or degree r(x) < degree g(x)]
6. A polynomial can have at most the same number of zeroes as the degree of the polynomial.
7. Relationship between zeroes and coefficients of a polynomial. If m and n are zeroes of p(x) ax² + bx + c (a ≠ 0), them Sum of zeroes = m + n = – b/a, Product of zeroes = mn = c/a
8. If m, n are zeroes of a quadratic polynomial p(x), then p(x) = k[x² – (sum of zeroes) x + product of zeroes] or p(x) = k [x² – (m + n)x +mn]; where k is any non-zero real number.
9. Graph of linear polynomial p(x) = ax + b is a straight line.
(i) If one zero of a quadratic polynomial p(x) is negative of the other, then coefficient of x = 0. (ii) If zeroes of a quadratic polynomial p(x) are reciprocal of each other, then co-efficient of x² = constant term.
IMPORTANT QUESTIONS BASED ON POLYNOMIALS
1. What will be the number of zeroes of a linear polynomial p(x) if its graph (i) passes through the origin. (ii) doesn’t intersect or touch x-axis at any point? [Answer: (i) 1, (ii) 0]
2. Find the quadratic polynomial whose zeroes are 5 + 2√3 and 5 – 2√3. [Answer: x² – 10x + 13]
3. For what value of p, is – 4 a zero of the polynomial x² – 2x – (7p + 3)? [Answer: 3]
4. If one zero of p(x) = 4x² – (8k2 – 40k) x – 9 is negative of the other, find values of k. [Answer: k = 0, 5]
5. What number should be added to the polynomial x² – 5x + 4, so that 3 is a zero of polynomial so obtained? [Answer: 2]
Download NCERT Books and Offline apps based on new CBSE Syllabus. Ask your doubts and share your knowledge with your friends and other users through Discussion Forum.
What are the total number of questions in exercise 2.1 Class 10 Maths?
There is only 1 question in exercise 2.1 of class 10th mathematics chapter 2 (Polynomials) and this question contain 6 parts and all parts of this question are important.
How many examples are based on exercise 2.1 in 10th mathematics?
Only 1 example with 6 parts is based on exercise 2.1 (chapter 2 Polynomials) of class 10th mathematics and all parts of this example are important.
What students will learn in exercise 2.1 Class 10th mathematics?
In exercise 2.1 (chapter 2 Polynomials) of class 10th mathematics students will learn how to find zeroes of polynomial p(x) using graph of y = p(x).
Is exercise 2.1 of class 10th mathematics easy or difficult?
Exercise 2.1 (chapter 2 Polynomials) of class 10th mathematics is easy exercise. But difficulty level of anything varies from student to student. So, Exercise 2.1 (chapter 2 Polynomials) of class 10th mathematics is easy or not depends on students also. Some students find it difficult some find it easy or very easy.