NCERT Solutions for Class 11 Maths Exercise 12.2 Limits and Derivatives in English and Hindi Medium updated for CBSE session 2025-26. The solutions of ex. 12.2 class 11 mathematics is revised according to new syllabus and rationalised NCERT books for academic year 2025-26.
Class 11 Maths Exercise 12.2 Solutions in Hindi and English Medium
NCERT Solutions for Class 11 Maths Exercise 12.2
| Class: 11 | Mathematics |
| Chapter: 12 | Exercise: 12.2 |
| Topic Name: | Limits and Derivatives |
| Content: | Exercise and Supplementary Solutions |
| Medium: | Hindi and English medium |
Application of Derivatives
The aforementioned Derivatives, limits, and algebraic equations are some of the major concepts that are being used to build the major technological marvels. Unlike polynomial equations or percentages, it is not something a person would do on daily bases.
The entire concept is being used to compute the precise velocity of spacecraft leaving Earth at different intervals by a rocket scientist, One can compute the time of the when the reservoir is going to be full by calculating the velocity of water or any fluid fills in a reservoir to avoid overflow.
Examples of Derivatives in Exercise 12.2 of 11th Maths
Post compliance of Algebra of limits and its sub-topics, like limits of polynomial and rational functions theorems, and trigonometric functions, you will study Derivatives again. The core of the matter is the derivatives of a function at a given point in its domain of definition.
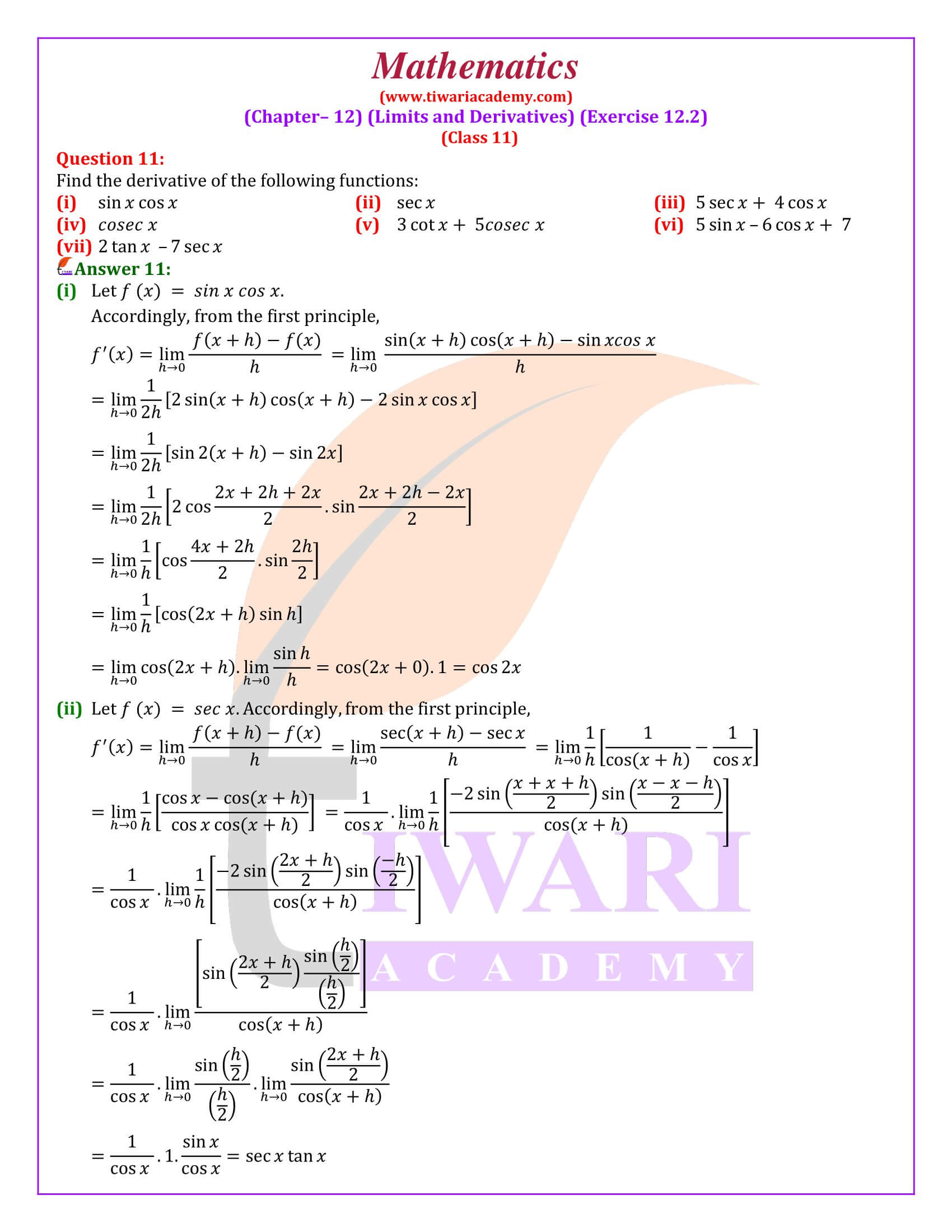
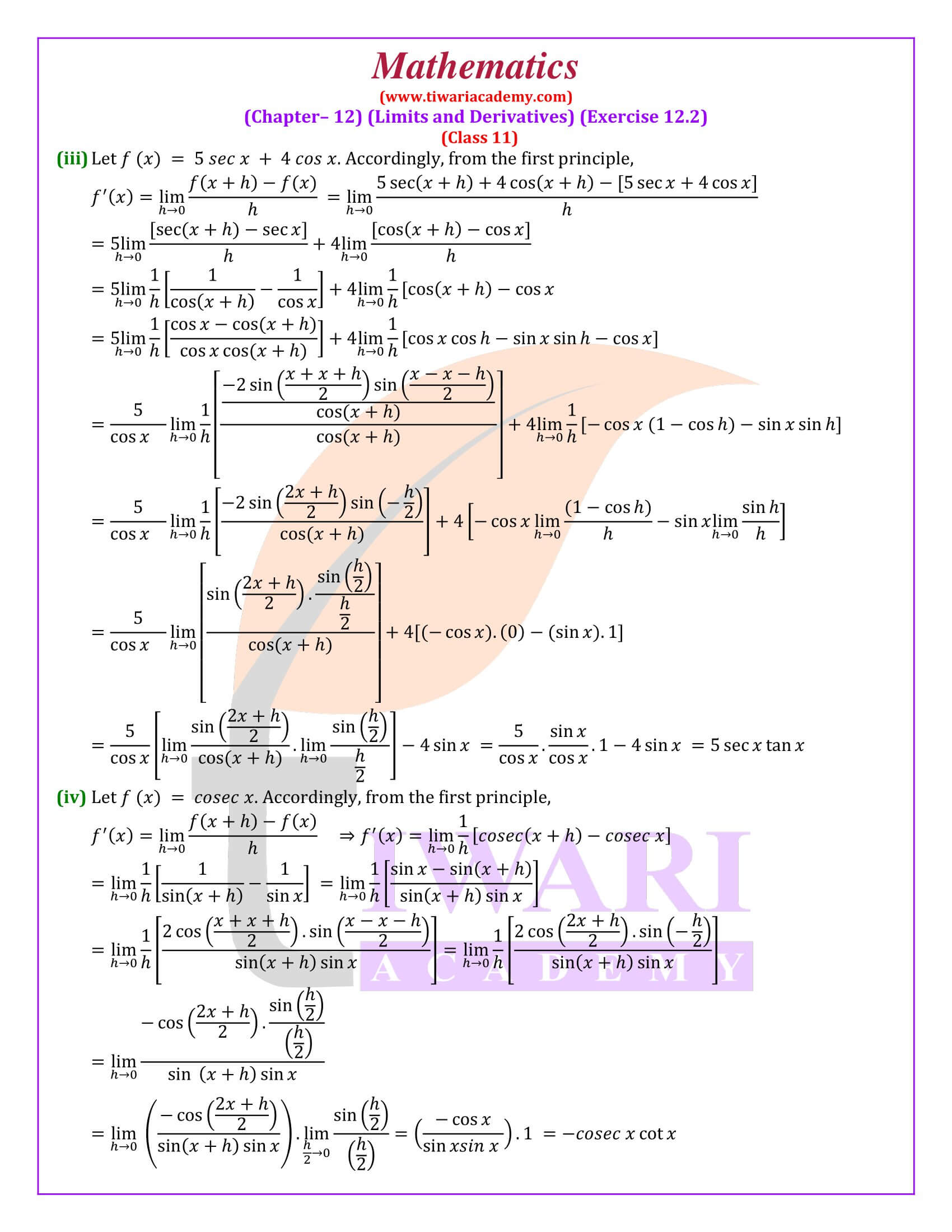
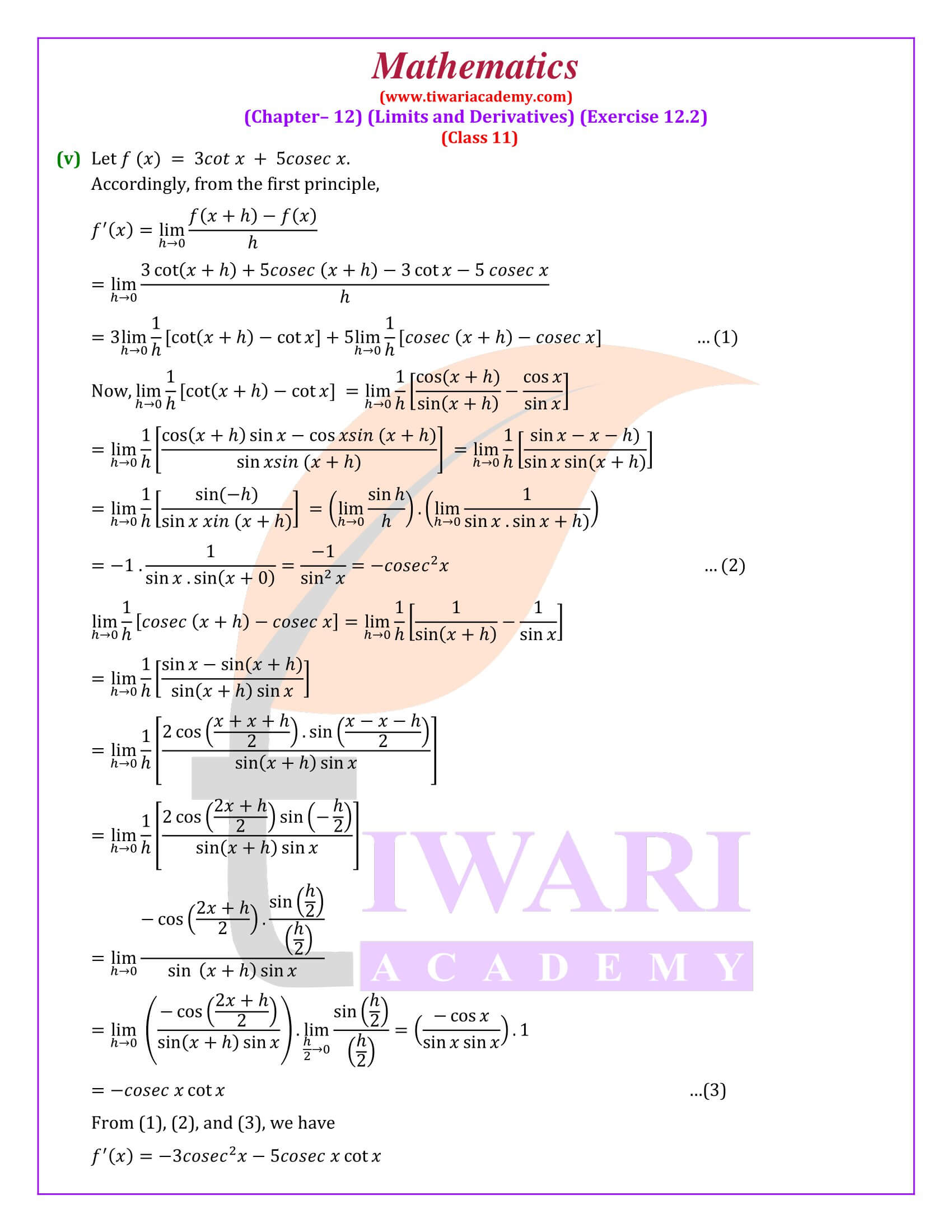
In the definition number 1 of derivatives, it states that let f be a real-valued function and a is a point in the domain of definition. The derivative of f at a can be obtained if limit exists. Derivatives of f(x) at a are denoted by f’(a). Here, the equation might look abstract now and would make sense in example number 5 of 11th Maths NCERT. Similarly, there will be 7 more examples given by using the concept to find different solutions.
Some main theorems and concepts
The second section of the chapter 12 contains a lot of theorems that will help you in the algebra of derivatives. It involves limits directly. Theorem 5 – 6 consists of some of the important rules that are directly connected with the next topic of derivatives of polynomials and trigonometry functions. Though, there are only 11 questions given in exercise 12.2 where you will be asked to solve questions using these concepts.
Application of First Principle in Exercise 12.2
It is advised to do all the questions of derivative using First Principle first time. Later on, you can implement direct formulae. The practice of derivatives using First Principle is important to learn the basic ways for derivation. In most of the mathematics exams, one or two questions are asked to solve using First Principle.