Class 12 Maths Exercise 2.1 Solutions
Class 12 Maths Exercise 2.2 Solutions
12th Maths Chapter 2 Miscellaneous Solutions
NCERT Solutions for class 12 Maths Chapter 2 Inverse Trigonometric Functions in Hindi and English Medium for revised and updated for 2024-25 exams. Class 12 Maths chapter 2 solutions are modified according to new NCERT books published for academic session 2024-25.
| Class: 12 | Mathematics |
| Chapter 2: | Inverse Trigonometric Functions |
| Study Material: | Exercise and Extra Questions |
| Content Mode: | Images, Text and Online Videos |
| Academic Session: | 2024-25 |
| Medium: | Hindi and English Medium |
Class 12 Maths Chapter 2 Solutions in English Medium
Class 12 Maths Chapter 2 Solutions in Hindi Medium

NCERT Solutions for class 12 Maths Chapter 2
Download the NCERT solutions of class xii Maths chapter 2 Hindi as well as English Medium free to use online or in PDF format including miscellaneous exercise and practice books based on NCERT Books with solutions and answers. Download offline apps based on latest CBSE Syllabus. The given NCERT Solutions Apps updated for new academic session 2024-25. The Previous Years Papers are to know the type and pattern of the questions asked which are designed as per latest CBSE Syllabus
Class 12 Maths Chapter 2 Study Material
Inverse Trigonometric Functions

We know that a function has inverse if and only if it is one – one and onto. There are many functions like trigonometric functions are not one – one or onto because these functions periodic so these are many one. In order to get inverse of these functions, we must restrict their domain and co-domain in such a way that they become one – one and onto and these restricted values are known as principle values.

There are some important theorems/ properties of inverse trigonometric functions. It is important to know that how to convert one function into the terms of others.
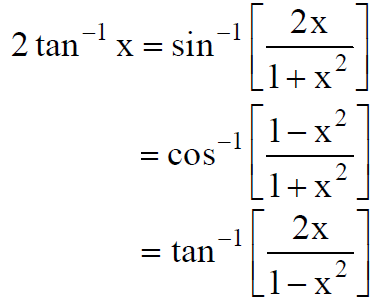
Complement functions are useful during the conversion of one functions into it complimentary functions.
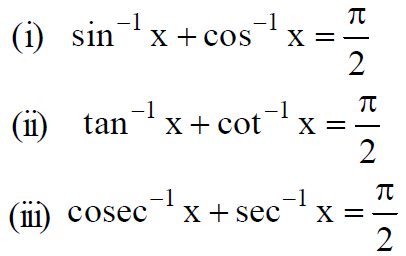
During the application of addition formula of tan, we should know that whether the product of x and y is greater than 1 or not. If it is more than 1, use the above formula and then apply the following formula.
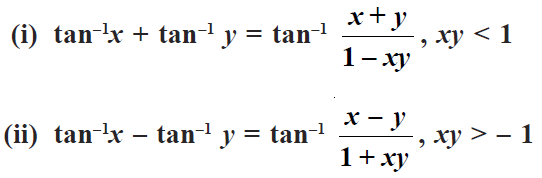
Important Questions on 12th Maths Chapter 2
Solve for x: 2 tan⁻¹(cos x) = tan⁻¹( 2cosec x)
Given that 2tan⁻¹(cosx) = tan⁻¹(2cosecx)
⇒ tan⁻¹(2cosx/(1-cos²x)) = tan⁻¹(2cosecx) [as 2 tan⁻¹x = tan⁻¹(2x/(1-x²)]
⇒ 2 cosx/(1 – cos²x) = 2cosecx
⇒ 2 cosx/(sin²x) = 2/sinx
⇒ 2 sin x.cos x = 2 sin² x
⇒ 2 sin x.cos x – 2 sin² x = 0
⇒ 2 sin x (cos x – sin x) = 0
⇒ 2 sin x = 0 or cos x – sin x = 0
But sin x ≠ 0 as it does not satisfy the equation.
∴ cos x – sin x = 0
⇒ cos x = sin x
⇒ tan x = 1
∴ x = π/4
Find the principal value of sin⁻¹(-1/2)
Let sin⁻¹(-1/2) = y, then sin y = -1/2 = – sin(π/6) = sin(-π/6)
We know that the range of the principal value branch of sin⁻¹ is [-π/2, π/2] and sin(-π/6) = -1/2
Therefore, the principal value of sin⁻¹(-1/2) is -π/6.
Find the principal value of tan⁻¹(−1).
Let tan⁻¹(−1) = y.
Then, tan y = -1 = – tan(π/4) = tan(-π/4)
We know that the range of the principal value branch of tan⁻¹ is (-π/2,π/2) and tan(-π/4) = -1
Therefore, the principal value of tan⁻¹(−1) is -π/4.
Trigonometry – Historical Facts!
The study of trigonometric functions started in 2nd millennium BC but in India it flourished in the Gupta Period due to Aryabhata. During the middle age, the study of trigonometry continued in Islamic Maths. The modern form of trigonometry functions were being used since 17th century by famous mathematician Isaac Newton, James Stirling etc.
What are the basic uses of inverse trigonometric functions chapter 2 of class 12th Mathematics?
The inverse trigonometric functions play an important role in calculus. The concepts of inverse trigonometric functions are also used in science and engineering. Inverse trigonometric functions are widely used in the navigation, physics, geometry, construction, and architecture. Also, an example of the use of inverse trigonometric functions in the real world is Carpentry.
What are the main points of chapter 2 of grade 12th Maths to remember at the time of board exams?
If students remember below mentioned points of chapter 2 of class 12th Maths on tips, they can quickly solve questions of chapter 2 in the board exams:
- Functions Domain Range (Principal Value Branches)
y=sin⁻¹x [-1,1] [-π/2, π/2]
y= cos⁻¹x [-1,1] [0, π]
y=cosec⁻¹x R-(-1,1) [-π/2, π/2]-{0}
y=sec⁻¹x R-(-1,1) [0, π]-{ π/2}
y=tan⁻¹x R (-π/2, π/2)
y=cot⁻¹x R (0, π) - sin⁻¹x should not be confused with (sin x)⁻¹. In fact (sin x)⁻¹=1/sin x and similarly for other trigonometric functions.
- Whenever no branch of an inverse trigonometric functions is mentioned, we mean the principal value branch of that function.
- The value of an inverse trigonometric functions which lies in the range of principal branch is called the principal value of that inverse trigonometric functions.
- All the properties of inverse trigonometric functions mentioned in section 2.3 of chapter 2 of class 12th Maths.
How many sums are there in chapter 2 of class 12th Maths in First Term Exam?
There are three exercises in chapter 2 of class 12th Maths.
In the first exercise (Ex 2.1), there are two examples (examples 1, 2) and 14 questions.
The second exercise (Ex 2.2) has 6 examples (Examples 3, 4, 5, 6, 7, 8) and 21 questions.
The last (Miscellaneous) exercise contains five examples (examples 9, 10, 11, 12, 13) and 17 questions.
So, there are in all 65 problems (13 examples and 52 questions) in chapter 2 of class 12th Maths.
What are the basic terms to understand chapter 2 of class 12th Maths easily?
To understand chapter 2 of class 12th Maths easily, students should revise below mentioned topics before starting chapter 2 of 12th Maths:
1. Chapter 3 (Trigonometric Functions) of class 11th Maths.
2. Invertible functions (chapter 1 of class 12th Maths).


