Class 12 Maths chapter 4 NCERT Solutions
Class 12th Maths Exercise 4.1 Solutions
Class 12th Maths Exercise 4.2 Solutions
Class 12th Maths Exercise 4.3 Solutions
Class 12th Maths Exercise 4.4 Solutions
Class 12th Maths Exercise 4.5 Solutions
Class 12th Maths Miscellaneous Exercise 4
The NCERT Solutions for class 12 Maths chapter 4 Determinants all exercise with miscellaneous in Hindi and English Medium new session 2024-25. The questions of each exercise is changed as per the new syllabus for CBSE 2024-25.
NCERT Solutions for class 12 Maths chapter 4
| Class: 12 | Mathematics |
| Chapter 4: | Determinants |
| Content: | NCERT Exercises Solution |
| Content Type: | Text, Videos and PDF Format |
| Session: | CBSE 2024-25 |
| Medium: | English and Hindi Medium |
Class XII Maths Chapter 4 solutions is given here. UP board solutions for class 12 Maths Chapter 4 are same as the NCERT Sols for 12th Maths Chapter 4. UP Board intermediate students are also using following NCERT Textbooks for new session, so they also can use these solutions for their help in problem solving. Other boards students like MP Board, Uttarakhand, and Gujrat Board can use these textbook solutions to prepare their exams. The solutions of questions are helpful for all the students who are using 12th NCERT Books. To understand the 12th Maths Chapter 4 properly, we must know everything about matrices. So, first learn the concepts of the chapter 3 Matrices to do Chapter 4 Determinants.
12th Maths Chapter 4 Solutions
In 12th Mathematics chapter 4 we shall study determinants up to order three only with real entries. The history about determinant is given below to know more about this fact. Download NCERT solutions for class 12 Maths chapter 4 determinants all six exercise with miscellaneous in PDF format. UP Board Solutions for Class 12 Maths Chapter 4 is same as NCERT Sols for 12th Maths Chapter 4 Determinants. So, UP Board students can also take the benefits of these solutions.

Class 12 Maths Chapter 4 Study Material
- Download Class 12 Maths NCERT Chapter 4
- Class 12 Maths Revision Book Chapter 4
- Class 12 Maths Revision Book Answers
- Class 12 Maths Download Assignment 1
- Class 12 Maths Download Assignment 2
- Class 12 Maths Download Assignment 2 Answers
- Class 12 Maths Download Assignment 3
- Class 12 Maths Download Assignment 4
- Class 12 Maths NCERT Solutions
- Class 12 all Subjects NCERT Solutions
Properties of Determinants
If all the rows of a determinant are converted into the corresponding columns, the value of the determinant remains same.
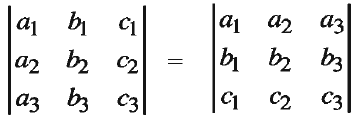
If two rows (columns) of a determinant are interchanged, the value of the new determinant is the additive inverse of the value of the given determinant.
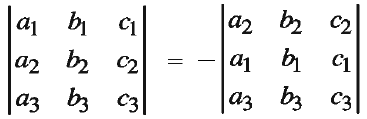
The value of a determinant gets multiplied by k, if every entry in any of its row (column) is multiplied by k.
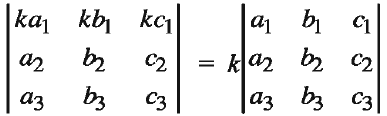
If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be express as sum of two (or more) determinants.
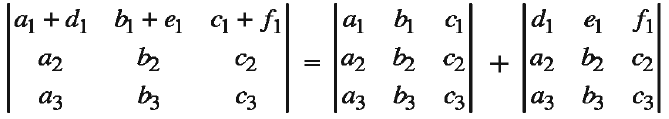
If the corresponding entries in any two rows ( or columns) are identical, the value of the determinant is zero.
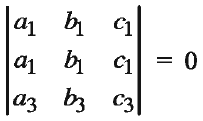
The value of a determinant does not changes if any of its rows (columns) is multiplied by non-zero real number k and added to another row (column).
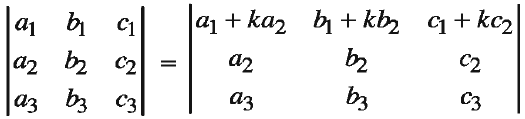
MINORS AND COFACTORS
Minor – Removing entries of the column and the row containing a given element of a determinant and keeping the surviving entries as they are, yields a determinant called the minor of the given element.
Cofactor – If we multiply the minor of an element by (-1)^(i+j), where i is the number of the row and j is the number of the column containing the element, then we get the cofactor of that element.
Historical Facts
- The Chinese early developed the idea of subtracting columns and rows as in simplification of a determinant using rods. Seki Kowa, the greatest of the Japanese Mathematicians of seventeenth century in his work ‘Kai Fukudai no Ho’ in 1683 showed that he had the idea of determinants as well as their expansion.
- T. Hayashi, “The Fakudoi and Determinants in Japanese Mathematics,” in the proc. of the Tokyo Math. Soc., V. Vendermonde was the first to recognise determinants as independent functions. He may be called the formal founder.
- Laplace (1772), gave general method of expanding a determinant in terms of its complementary minors.
- Lagrange, in 1773, treated determinants of the second and third orders and used them for purpose other than the solution of equations.
- Gauss, in 1801, used determinants in his theory of numbers.
- Jacques – Philippe – Marie Binet, in 1812, stated the theorem relating to the product of two matrices of m-columns and n-rows, which for the special case of m = n reduces to the multiplication theorem.
- Cauchy, in 1812, presented one on the same subject. He used the word ‘determinant’ in its present sense. He gave the proof of multiplication theorem more satisfactory than Binet’s.
- The greatest contributor to the theory was Carl Gustav Jacob Jacobi, after this the word determinant received its final acceptance.
In which practical fields can students use determinants chapter 4 of 12th Maths?
Determinants have wide applications in Engineering, Science, Economics, Social Science, etc. Determinants have wonderful algebraic properties and occupied their proud place in linear algebra because of their role in higher-level algebraic thinking.
Which main topics will students study in chapter 4 of class 12th Maths?
In chapter 4 of class 12th Maths, students will study determinants up to order three only with real entries. Also, students will study various properties of determinants, minors, cofactors and applications of determinants in finding the area of a triangle, adjoint and inverse of a square matrix, consistency and inconsistency of the system of linear equations and solution of linear equations in two or three variables using the inverse of a matrix.
Can students do chapter 4 Determinants of 12th Maths without going through chapter 3?
Students can’t do chapter 4 of class 12th Maths without doing chapter 3 of class 12th Maths. Before starting chapter 4, Determinants of class 12th Maths, students should first do chapter 3 Matrices of grade 12th Maths. Chapter 3 Matrices of class 12th Maths works as a base for chapter 4 Determinants of grade 12th Maths.
Does chapter 4 of grade 12th Maths has any miscellaneous exercise?
Chapter 4 of grade 12th Maths has a miscellaneous exercise. There are six exercises in chapter 4 of class 12th Maths, and the last exercise is the miscellaneous exercise of chapter 4 of grade 12th Maths. In the first exercise, there are eight questions. The second exercise has 16 questions. The third exercise contains five questions. There are five questions in the fourth exercise. In the fifth exercise, there are 18 questions. There are 19 questions in the last (Miscellaneous) exercise.


