NCERT Textbook Solutions for Class 12 Mathematics Chapter 3 Matrices for Session 2025-26, an essential topic in Class 12 Maths, form the backbone of many advanced mathematical concepts. Chapter 3 of the NCERT Maths textbook explore this fascinating world, starting with the basic definition of matrices and their types. A matrix is essentially a rectangular array of numbers arranged in rows and columns. NCERT Detailed Solutions for Class 12 Textbook Matrices offer a step-by-step approach to solving Exercise 3.1 and Exercise 3.2, which cover topics like the order of matrices and equality of matrices. With solved examples and practice questions, students can easily grasp the core concepts.
NCERT Textbook Solutions for Class 12 Maths Chapter 3 Matrices
Understanding matrices is vital for solving problems in linear algebra and real-world applications like computer graphics. NCERT Class 12th Mathematics solutions also highlight important properties and key formulas, making it easier to revise and apply the concepts during exams. Get here modified NCERT Solutions for Class 12 Maths Chapter 3 Matrices in English and Hindi Medium updated for academic session 2025-26. The question answers and solutions are revised according to new NCERT books published for 2025-26 board exams.
Class 12 Maths Chapter 3 MCQ Solutions
Exploring Operations on Matrices in 12th Mathematics
Operations on matrices, such as addition, subtraction and multiplication, are a key focus in Chapter 3 of Class 12 Mathematics. NCERT Textbook Solutions for Exercise 3.3 simplify these operations through solved examples and practical problems. Class 12th NCERT Mathematics solutions emphasize the importance of understanding rules, such as the non-commutative nature of matrix multiplication. Properties like the associative and distributive laws are also explained to strengthen conceptual understanding.
For instance, while adding matrices, their orders must match, and for multiplication, the number of columns in the first matrix must equal the number of rows in the second. These mathematical approaches, combined with practice, help students solve NCERT Textbook Exercise 3.3 efficiently. The NCERT Maths Book Matrices Chapter PDF also includes detailed examples to help students learn how to find the transpose and inverse of matrices, main topics for competitive exams and higher studies.
Class 12 Math Chapter 3 Solutions in Hindi Medium
Applications and Problem-Solving in 12th Mathematics as Matrices
Matrices are not just theoretical; their applications span across various fields like engineering, physics and economics. Chapter 3 Class 12 NCERT Textbook Mathematics introduces advanced topics like finding the determinant and adjoint of a matrix, which are extensively used in solving systems of linear equations. NCERT Complete Solutions for Exercises 3.4 provide a detailed mathematical approach to these concepts, breaking them into smaller, manageable steps.
Solved examples in the chapter show how to use matrices to represent and solve real-world problems, making the topic highly practical. Key formulas are highlighted for quick revision. With practice, students can confidently tackle questions related to properties of determinants and the inverse of a matrix. This solid foundation ensures success not just in board exams but also in future academic endeavors.
| Class: 12 | Mathematics |
| Chapter 3: | Matrices |
| Number of Exercises: | Five (4 + Miscellaneous) |
| Content: | Textbook and Extra Questions |
| Content Mode: | Images, Text, PDF and Online Videos |
| Academic Session: | 2025-26 |
| Medium: | English and Hindi Medium |
Class 12 Maths Chapter 3 Solutions in English Medium
Important Points in Class 12 Maths Chapter 3 Matrices for Exams
1. Definition and types of matrices.
2. Operations: addition, subtraction, multiplication, scalar multiplication.
3. Properties: associative, distributive and commutative laws, Transpose of a matrix.
4. Determinants, adjoint and inverse of matrices.
5. Application of matrices in solving linear equations.
| Day | Topic | Tasks |
|---|---|---|
| Day 1 | Introduction to Matrices | Read NCERT theory, solve examples from Exercise 3.1 |
| Day 2 | Types of Matrices and Equality | Practice Exercise 3.1 questions |
| Day 3 | Matrix Operations | Solve Exercise 3.2, focus on addition and multiplication rules |
| Day 4 | Transpose and Properties | Revise key formulas, solve questions from Exercise 3.3 |
| Day 5 | Determinants and Adjoint | Learn the process to find determinants and adjoints, solve examples |
| Day 6 | Inverse of a Matrix | Focus on Exercise 3.4 and key formulas like \( A \times A^{-1} = I \) |
| Day 7 | Revision and Practice | Solve mixed questions from all exercises and revise key points |
Class 12 Maths Chapter 3 Solutions are useful for CBSE and UP Board students, they can download these plus two solutions in PDF format free otherwise use online these updated solutions for the new academic session 2025-26. In Uttar Pradesh now NCERT Textbooks are implemented for class 12, so students of 10+2 can use these UP Board Solution for Class 12 Maths Chapter 3. In every question of 12th Maths Chapter 3 Matrix, the explanation of each step is given. The step by step solutions for plus two Maths is given with video solution and text file format. Madhya Pradesh and Gujrat Board are also following Textbooks of NCERT. So, these solutions of 12th Maths Chapter 3, is important not only for CBSE or UP Board Students, but the other boards also who are using 12th NCERT Textbooks as current course books.
12th Maths Chapter 3 Solutions
Download NCERT Solutions Class 12 Maths chapter 3 exercise 3.1, 3.2, 3.3, 3.4 and miscellaneous exercises in English and Hindi Medium for CBSE Board. UP Board Students are using the same NCERT Books, so they can also use these solutions as UP Board Solutions 12 Maths Chapter 3 for the academic session 2025-26. We have done everything perfectly to provide solutions of Class 12 Maths for CBSE and UP Board, if you feel some problem, inform us. We will definitely rectify.
Class 12 Maths Chapter 3 Study Material
- Class 12 Maths NCERT Book Chapter 3
- Download 12th Maths Revision Book Chapter 3
- Download 12th Maths Revision Book Answers
- Download Class 12 Maths Chapter 3 Assignment 1
- Download Class 12 Maths Chapter 3 Assignment 2
- Download Class 12 Maths Chapter 3 Assignment 2 Answers
- Download Class 12 Maths Chapter 3 Assignment 3
- Download Class 12 Maths Chapter 3 Assignment 4
- Class 12 Maths NCERT Solutions
- Class 12 all Subjects NCERT Solutions
Matrix
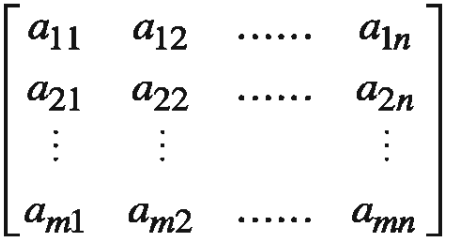
The arrangement of real numbers in a rectangular array enclosed in brackets as [] or () is known as a Matrix (Matrices is plural of matrix). Matrix operations are used in electronic physics, computers, budgeting, cost estimation, analysis and experiments. They are also used in cryptography, modern psychology, genetics, industrial management etc. In general an m x n matrix is matrix having m rows and n columns. it can be written as follows:
Important Terms related to 12th Maths Chapter 3
- Order of a Matrix
There may be any number of rows and any number of columns in a matrix. If there are m rows and n columns in matrix A, its order is m x n and it is read as an m x n matrix. - Transpose of a Matrix
The transpose of a given matrix A is formed by interchanging its rows and columns and is denoted by A’. - Symmetric Matrix
A square matrix A is said to be a symmetric matrix if A’ = A. - Skew-Symmetric Matrix
A square matrix A is said to be a skew symmetric if A’ = – A. all elements in the principal diagonal of a skew symmetric matrix are zeroes. - Addition of Matrix
If A and B are any two given matrices of the same order, then their sum is defined to be a matrix C whose respective elements are the sum of the corresponding elements of the matrices A and B and we write this as C = A + B.
Types of Matrices
- Row matrix: A row matrix has only one row but any number of columns.
- Column matrix: A column matrix has only one column but any number of rows.
- Square matrix: A square matrix has the number of column equal to the number of rows.
- Rectangular Matrix: A matrix is said to be a rectangular matrix if the number of rows is not equal to the number of columns.
- Diagonal matrix: If in a square matrix has all elements 0 except principal diagonal elements, it is called diagonal matrix.
- Scalar Matrix: A diagonal matrix is said to be a scalar matrix if all the elements in its principal diagonal are equal to some non-zero constant.
- Zero or Null matrix: If all elements of a matrix are zero, then the matrix is known as zero matrix and denoted by O.
- Unit or Identity matrix: If in a square matrix has all elements 0 and each diagonal elements are non-zero, it is called identity matrix and denoted by I.
- Equal Matrices: Two matrices are said to be equal if they are of the same order and if their corresponding elements are equal.
Properties of Matrices
- When a matrix is multiplied by a scalar, then each of its element is multiplied by the same scalar.
- If A and B are any two given matrices of the same order, then their sum is defined to be a matrix C whose respective elements are the sum of the corresponding elements of the matrices A and B and we write this as C = A + B.
- For any two matrices A and B of the same order, A + B = B + A. i.e. matrix addition is commutative.
- For any three matrices A, B and C of the same order, A + (B + C) = (A + B) + C i.e., matrix addition is associative.
- Additive identity is a zero matrix, which when added to a given matrix, gives the same given matrix, i.e., A + O = A = O + A.
- If A + B = O, then the matrix B is called the additive inverse of the matrix of A.
- If A and B are two matrices of order m x p and p x n respectively, then their product will be a matrix C of order m x n.
Invertible Matrix
A square matrix of order n is invertible if there exists a square matrix B of the same order such that AB = I = BA, Where I is identify matrix of order n.
Theorems of invertible matrices
- Theorem 1: Every invertible matrix possesses a unique inverse.
- Theorem 2: A square matrix is invertible iff it is non-singular.
Historical Facts! about Matrix
Matrix is a latin word. Originally matrices are used for solutions of simultaneous linear equations in Mathematics. An important Chinese Text between 300 BC and 200 AD, nine chapters of Mathematical Art(Chiu Chang Suan Shu), give the use of matrix methods to solve simultaneous equations. Carl Friedrich Gauss(1777 – 1855) also gave the method to solve simultaneous equations by matrix method.
Why are Matrices important in Class 12 Maths?
Matrices are rectangular arrays of numbers arranged in rows and columns, forming the basis of Chapter 3 in Class 12 Mathematics. They are important because they help solve complex problems in linear algebra and real-world scenarios, such as computer graphics and data analysis. The NCERT Solutions for Class 12 Matrices provide detailed explanations of NCERT Exercise 3.1 and Exercise 3.2, focusing on fundamental topics like the order and equality of matrices. Understanding matrices is essential for building advanced concepts like determinants, adjoints and inverses, which are critical for higher studies and competitive exams.
What does chapter 3 of class 12th Maths explore about Matrix?
A matrix is an ordered rectangular array of numbers or functions. The numbers or functions are called the elements or the entries of the matrix. We denote matrices by capital letters.
The following are some examples of matrices: –
In the above examples, the horizontal lines of elements are said to constitute, rows of the matrix and the vertical lines of elements are said to constitute, columns of the matrix. Thus A has 3 rows and 2 columns and B has 3 rows and 3 columns.
What operations on matrices are covered in Chapter 3 of Class 12 Maths?
Chapter 3 in Class 12 Maths covers various operations on matrices, such as addition, subtraction, multiplication and scalar multiplication. NCERT Simplified Solutions for Exercise 3.3 simplify these operations with step-by-step examples. For instance, addition and subtraction require matrices to have the same order, while multiplication depends on the compatibility of rows and columns. NCERT Class 12th Mathematics solutions also explain important properties like associative and distributive laws, which are vital for solving complex problems. By practicing these operations through the NCERT Maths Matrices Chapter, students can develop a deeper understanding of these mathematical concepts.
What are the practical implimentations of matrices chapter 3 of 12th Maths in different fields?
The knowledge of matrices is necessary in various branches of mathematics. Matrices are one of the most powerful tools in mathematics. The evolution of the concept of matrices is the result of an attempt to obtain compact and simple methods of solving a system of linear equations. Matrix notation and operations are used in electronic spreadsheet programs for personal computer, which in turn is used in different areas of business and science like budgeting, sales projection, cost estimation, analyzing the results of an experiment, etc.
Also, many physical operations such as magnification, rotation, and reflection through a plane can be represented mathematically by matrices. Matrices are also used in cryptography. This mathematical tool is not only used in certain branches of sciences but also in genetics, economics, sociology, modern psychology, and industrial management.
How does the NCERT Solutions for Class 12 Matrices help in solving Exercise 3.4?
NCERT Mathematics Solutions for Class 12 Matrices provide a clear and structured approach to solving Exercise 3.4, which focuses on finding determinants, adjoints and inverses of matrices. These topics are critical for solving systems of linear equations and appear frequently in board exams. NCERT 12th Mathematics solutions explain key formulas and break down the steps required to compute these values. By practicing with solved examples and revision questions, students can master these concepts and apply them in real-world scenarios like physics and engineering problems.
How many exercises are there in chapter 3 of class 12th Maths for 1st term exam?
There are 5 exercises in chapter 3 of class 12th Maths. The first exercise (Ex 3.1) has 15 sums (5 examples and 10 questions). The second exercise (Ex 3.2) contains 36 sums (14 examples and 22 questions). In the third exercise (Ex 3.3), there are 15 sums (3 examples and 12 questions). The fourth exercise has 21 sums (3 examples and 18 questions). There are 18 sums (3 examples and 15 questions) in the last (Miscellaneous) exercise.
What is the significance of solved examples in understanding Chapter 3 Matrices?
Solved examples play a crucial role in helping students understand the concepts covered in Chapter 3 Matrices. The NCERT Textbook Solutions for Class 12 Matrices include examples that explain operations like addition, multiplication and transposition in detail. These examples also demonstrate how to use properties like associative and distributive laws while solving Exercise 3.3 and NCERT Exercise 3.4. By practicing these examples, students gain confidence in handling complex problems and learn to avoid common mistakes. NCERT Mathematics Book Matrices Chapter PDF provides additional practice questions to strengthen problem-solving skills and prepare for board exams effectively.
Are there any theorems in chapter 3 of class 12th Maths?
Yes, there are four theorems in chapter 3 of class 12th Maths. All the theorems are nice, easy, and important. Proofs of these theorems are short and easy. Students can easily understand the theorems and proofs of these theorems.
How can matrices be applied in real-world problems?
Matrices have significant applications in real-world problems, including computer graphics, physics, economics and data analysis. Chapter 3 of Class 12 Maths introduces concepts like determinants, adjoints and inverses, which are used to solve systems of linear equations. NCERT Solutions for Exercises 3.4 provide practical examples of these applications, breaking down the steps for clarity. For instance, matrices can represent transformations in graphics or optimize resource allocation in economics. By mastering the properties and operations of matrices, students can build a strong foundation for advanced studies and apply their knowledge to solve practical problems efficiently.


