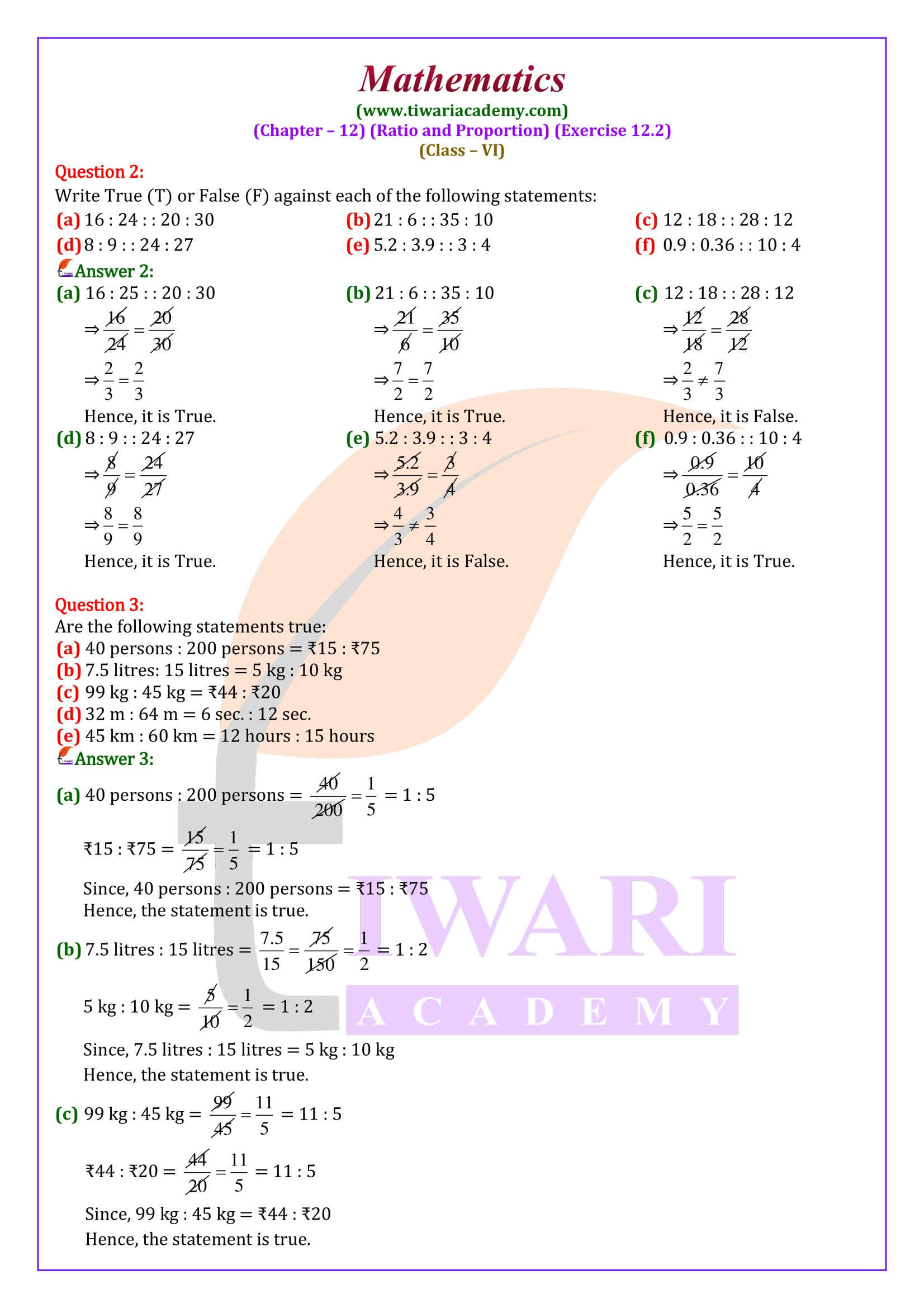
NCERT Solutions for Class 6 Maths Chapter 12 Exercise 12.2 in Hindi and English Medium updated for CBSE session 2024-25. Get here the revised solutions of ex. 12.2 class 6th Maths based on new syllabus and NCERT books for academic session 2024-25.
6th Maths Exercise 12.2 Solutions in Hindi and English Medium
| Class: 6 | Mathematics |
| Chapter: 12 | Exercise: 12.2 |
| Chapter Name: | Ratio and Proportion |
| Content: | NCERT Book Solution |
| Session: | Academic Year 2024-25 |
| Medium: | Dual Language – English and Hindi |
Class 6 Maths Chapter 12 Exercise 12.2 Solution
Class VI Mathematics chapter 12 Ex. 12.2 solution Ratio and Proportion in Hindi and English prepared for CBSE Board students academic session 2024-25. All the contents are given in videos and PDF file format free to access online or download. In class 6 math NCERT (https://ncert.nic.in/) Book exercise 12.2 questions are based on proportion and its properties. It also tell how to use proportion in daily life situations. Most of the questions in NCERT Books of 6th math ex. 12.2 are interesting to solve.
Class 6 Maths Chapter 12 Exercise 12.2 Solution in Videos
Proportion
We know that ¼ and 2/8 are equivalent fractions.
So, 1 : 4 = 2 : 8
Similarly, 6 : 18 = 12 : 36
And 25 : 10 = 100 : 40
Each of the above statements expresses the equality of two given ratios.
An equality of two ratios is called proportion.
In general, four numbers a, b, c, d are said to be in proportion, if the ratio of the first two is equal to the ratio of the last two, i.e., a : b = c : d. This is equivalent to a/b = c/d, i.e., ad = bc.
The equality “3 :5 = 6 :10” forms a proportion. We sometimes write “3 : 5 = 6 : 10” as “3 : 5 :: 6 : 10”, which is read as “3 is to 5 as 6 is to 10” or “3 to 5 as 6 to 10”.
A proportion consists of four terms. The first and the fourth terms of the proportion are called extreme terms or extremes. The second and the third terms are called middle terms or means.
| Proportion | Product of the extremes | Product of means |
|---|---|---|
| 1 : 2 = 2 : 4 | 1 × 4 = 4 | 2 × 2 = 4 |
| 5 : 12 = 15 : 36 | 5 × 36 = 180 | 12 × 15 = 180 |
| 27 : 45 = 18 : 30 | 27 × 30 = 810 | 45 × 18 = 810 |
| 128 : 16 = 48 : 6 | 128 × 6 = 768 | 16 × 48 = 768 |
What do we conclude? We conclude that in a proportion, the product of the extremes is equal to the product of the means. In other words, a : b = c : d if and only if ad = bc.
Class 6 Maths Exercise 12.2 Important Questions
Check whether the given ratios are equal, i.e., they are in proportion: (i) 3 : 7 and 12 : 21, (ii) 14 : 8 and 42 : 24, (iii) 31 : 5 and 15 : 2
(i) Product of extremes = 3 × 21 = 63
Product of means = 7 × 12 = 84
Since, the product of extremes ≠ product of means,
Therefore 3 : 7 and 12 : 21 are not in proportion.
(ii) Product of extremes = 14 × 24 = 336
Product of means = 8 × 42 = 336
Since, the product of extremes = product of means,
Therefore, the two ratios are in proportion.
(iii) Product of extremes = 31 × 2 = 62
Product of means = 5 × 15 = 75
Since, the two product are not equal,
Therefore, the two ratios are not in proportion.
How are proportions used in real life?
The business can use proportions to figure out how much money they will earn if they sell more products. If the company sells ten products, for example, the proportional ratio is Rs. 25.00:10, which shows that for every ten products, the business will earn Rs. 25.
What are the different types of proportion?
There are two types of proportions.
(i) Direct Proportion.
(ii) Inverse Proportion.
The second, third and fourth terms in a proportion are 15, 8, 12 respectively. Find the first term.
Let the first term be x.
Then x, 15, 8 and 12 are in proportion.
So, x × 12 = 15 × 8
Or, x = 120/12 = 10.
Thus, the first term is 10.
Note: If in an arrangement of four numbers, the product of their extremes is not equal to the product of their means, we say that the four numbers in that order are not in proportion.
Which questions and examples of exercise 12.2 of 6th class Maths can the teacher give in the unit test?
Exercise 12.2 of 6th class Maths contains 4 questions and 3 examples (examples 8, 9, and 10). Question 4 and example 10 of this exercise are significant, and the teacher can give these problems in the unit test.
Is exercise 12.2 of 6th class Maths little bit lengthy?
Exercise 12.2 of 6th class Maths contains 4 questions and 3 examples (examples 8, 9, and 10) only. This exercise is short and not lengthy. Students require only one day to complete exercise 12.2 of 6th class Maths. This time can vary because it depends on the student’s working speed, ability, efficiency, etc.
What type of questions can come from exercise 12.2 of 6th class Maths?
From exercise 12.2 of 6th class Maths, Short answer type questions like MCQ, fill in the blanks, true or false, one-word answer, yes or no, match them, etc can come in the exams. One mark or more than one mark question can come from this exercise in the exams.
What will students learn in exercise 12.2 of 6th class Maths?
In exercise 12.2 of 6th standard Maths, students will learn the meaning of proportion (If two ratios are equal, we say that they are in proportion and use the symbol ‘::’ or ‘=’ to equate the two ratios).