NCERT Solutions for Class 6 Maths Chapter 12 Exercise 12.1 in Hindi and English Medium updated for CBSE 2024-25 session. All the questions of ex. 12.1 class 6th Maths revised according to rationalised syllabus and new NCERT books for CBSE 2024-25.
6th Maths Exercise 12.1 Solutions in Hindi and English Medium
| Class: 6 | Mathematics |
| Chapter: 12 | Exercise: 12.1 |
| Chapter Name: | Ratio and Proportion |
| Mode of Content: | Text and Videos Format |
| Session: | CBSE 2024-25 |
| Medium: | Hindi and English Medium |
Class 6 Maths Chapter 12 Exercise 12.1 Solution
Class VI Mathematics Ex. 12.1 solution Ratio and Proportion designed for CBSE new session 2024-25 free to download. All the question answers are given in PDF file format and videos format. Class 6 Maths NCERT (https://ncert.nic.in/) Book exercise 12.1 contains the questions based on ratio and its application. Questions based on daily life related to ratios are given here, so that CBSE and state board student can get better practice in ratios and its application.
Class 6 Maths Chapter 12 Exercise 12.1 Solution in Videos
Comparison of Quantities in Terms of Their Magnitudes and Measurements
(i) By finding the difference of the magnitudes of two quantities. This is known as the comparison by difference.
(ii) By finding the division of the magnitudes of two quantities. This is known as the comparison by division.
Comparison by Difference
If Rohan and Dinesh are two students of 9th standard, having their weights as 55 kg and 45 kg respectively, then we can say that Rohan’s weight is greater than Dinesh’s weight by (55 – 45) kg = 10 kg. Similarly, if Rohan’s height is 156 cm and that of Dinesh’s is 144 cm, then we may say that Rohan is taller than Dinesh by (156 – 144) cm, i.e., by 12 cm. Thus, we have compared weights and heights of Rohan and Dinesh by finding difference between them. Such a comparison is known as the comparison by difference.
Consider another example:
Cost of a car is Rs. 240000 and that of a scooter is Rs. 40000. If we calculate the difference between the costs, it is Rs. 200000 and if we compare by division; that is 240000/40000 = 6/1.
We can say that the cost of the car is six times the cost of the scooter. Thus, in certain situations, comparison by division makes better sense than comparison by taking the difference.
Comparison by Division
Weight of Rohan and Dinesh can also be compared by finding their division.
We have, weight of Rohan/ weight of Dinesh 55/45 = 11/9
So, we can say Rohan’s weight is 11/9 times the weight of Dinesh.
We have, height of Rohan/ height of Dinesh 156/144 = 13/12
So, we can say Rohan’s height is 13/12 times that of Dinesh. We can also say that Rohan is 13/12 times taller than Dinesh. Such a comparison is known as comparison by division.
Usually, we use the symbol: to express a ratio.
Therefore, the ratio of the height of Rohan to that of Dinesh is written as 156 :144 and read as ‘156 is to 144′ or 156 to 144’.
In general, we can define the term ‘ratio’ as under:
The ratio of two quantities of the same kind and in the same units is the fraction that one quantity is of the other. Thus, the ratio of two numbers a and b (b ≠ 0) is a ÷ b or and is denoted by a: b.
The numbers a and b in the ratio a: b are known as first term or antecedent and second term or consequent respectively.
Ratio in the Simplest Form
When the two terms of a ratio have no common factor other than 1, we say that the ratio is in the simplest form. Usually, a ratio is expressed in the simplest form.
Class 6 Maths Exercise 12.1 Important Questions
Give two equivalent ratios of 12: 8.
Ratio 12: 8 = 12/8 = 3/2
Therefore, 3: 2 is an equivalent ratio of 12: 8.
Similarly, the ratio 12: 8 = 12/8 = 24/16
So, 24: 16 is another equivalent ratio of 12: 8.
How are ratios used in real life?
Common examples include comparing prices per ounce while grocery shopping, calculating the proper amounts for ingredients in recipes and determining how long car trip might take. Other essential ratios include pi and phi (the golden ratio).
How do you interpret ratios in math?
A ratio is an ordered pair of numbers a and b, written a/b where b does not equal 0.
For example, if there is 1 boy and 3 girls you could write the ratio as:
(i) 1 : 3 (for every one boy there are 3 girls)
(ii) 1/4 are boys and 3/4 are girls.
(iii) 0.25 are boys (by dividing 1 by 4)
(iv) 25% are boys (0.25 as a percentage)
Two numbers are in the ratio 3 :5. If the sum of the numbers is 128, find the numbers.
Let the numbers be 3x and 5x.
Then, we have, 3x + 5x = 128
Or, 8x = 128
Or, x = 16
So, 3x = 3 × 16
= 48 and
5x = 5 × 16
= 80.
Notes:
- The comparison of two quantities is meaningful only when they are of same kind, i.e., measured in the same units. It is just meaningless to compare 25 km to 40 kg.
- Since the ratio of two quantities of the same kind determines how many times one quantity is contained by the other. Therefore, the ratio of any two quantities of same kind is an abstract quantity.
- In a ratio, the order of the terms is very important. For example, the ratio 4: 3 is different from the ratio 3: 4.
Which questions of exercise 12.1 Class 6 Maths students can mark as important?
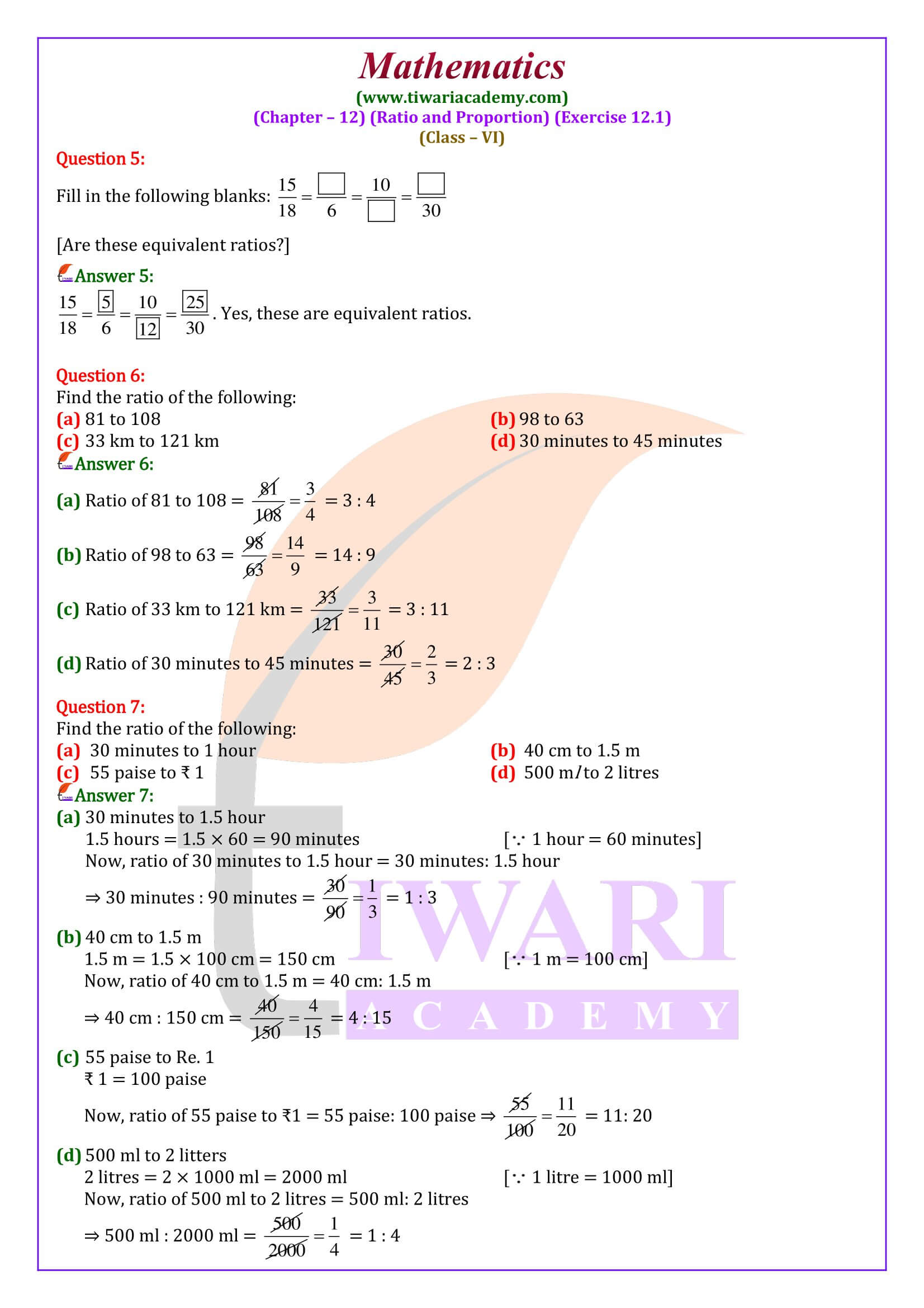
Exercise 12.1 of 6th grade Maths has 16 questions. Out of these 16 questions, 5 questions of exercise 12.1 are important. These important questions are questions 5, 7, 12, 13, and 16. These questions have more chances compared to the other questions of this exercise to come in the exams.
Which questions of exercise 12.1 of 6th standard Maths are easy to understand?
Exercise 12.1 of 6th grade Maths has 16 questions. Questions 1, 2, 3, 4, 6, 8, 9, and 10 of exercise 12.1 of 6th standard Maths are easy to solve and understand. These questions are straightforward and not tricky.
Which questions of exercise 12.1 of 6th standard Maths are complicated to solve?
Exercise 12.1 of 6th grade Maths has 16 questions. Questions 5, 7, 11, 12, 13, 14, 15, and 16 of exercise 12.1 of 6th standard Maths are not easy to solve and understand. These questions are complicated to solve and understand. These questions are a little tricky.
How many illustrations are there in exercise 12.1 of 6th class Maths?
In exercise 12.1 of 6th standard Maths, there are seven illustrations (examples 1, 2, 3, 4, 5, 6, and 7). Examples 3, 5, and 7 of this exercise are important. Examples 3, 5, and 7 have a chance to come to the exams.