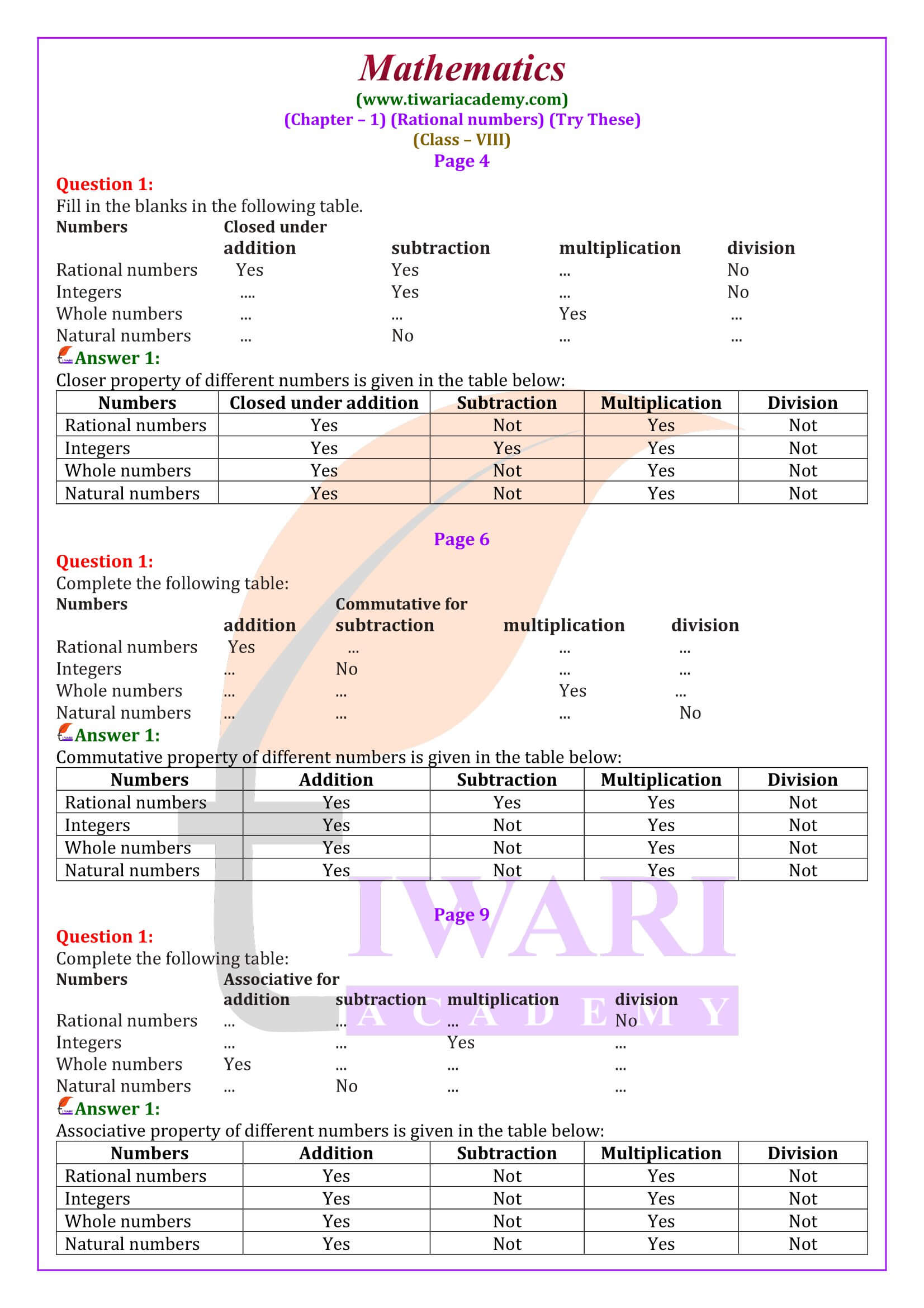
Class 8 Maths Chapter 1 Try These
Class 8 Maths Exercise 1.1 Solutions
Class 8 Maths Exercise 1.1 in Hindi
Get the best NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers and Class 8 Maths Chapter 1 Try These Solution in Hindi and English Medium modified and updated for academic year 2024-25. As per the revised new syllabus 2024-25 for class 8th Maths, there is only one exercise in chapter 1 rational numbers.
8th Maths Chapter 1 Solutions for CBSE Board
8th Maths Chapter 1 Solutions for State Boards
NCERT Solutions for Class 8 Maths Chapter 1
Tiwari Academy gives the solutions of Prashnavali 1.1 in Hindi. CBSE Students can download Exercise 1.1 in English Medium. All the solutions are free to download in PDF. We have updated it for CBSE and State Boards. We offer Offline Solutions apps for Class 8 Maths in Hindi English Medium. Join the Discussion Forum to ask the difficult sums and puzzles in Maths.

| Class: 8 | Mathematics |
| Chapter 1: | Rational Numbers |
| Number of Exercises: | 1 (One) |
| Content: | NCERT Exercises Solution |
| Mode of content: | Videos and Online Text Format |
| Session: | 2024-25 |
| Medium: | Hindi and English Medium |
Class 8 Maths Chapter 1 Solutions
Study online Exercise 1.1 of Rational Numbers class 8 Maths Solutions in English and Hindi Medium here. Click to Exercise 1.1 in English or Prashnavali 1.1 in Hindi. Video Format solutions of each exercise are also available to use free.
More about Class 8 Maths Chapter 1
8th Maths Chapter 1 deals with the use of various terms of simple Maths. It teaches about property of addition, subtraction and Products. We will work on Commutative and other properties. Learn the rules are under addition and Product. In all the ways we have to check terms. For example, if Identity, Inverse exist or not.
Student learn here the use of additive identity or inverse. We work on the approach of distributive property. We learn here the ways to show rational number on a number line. Get the rational number between any two rational numbers. We know that there are countless rational numbers between two. Using the idea of mean, we find the numbers between two rational numbers.

Class 8 Maths Chapter 1 Important Questions
Are the Rational Numbers closed under the operations of Division?
No, the Rational numbers are closed under addition, subtraction and multiplication operations only.
Which rational number is additive identity for all rational numbers.
Zero (0) is the additive identity for rational numbers.
How many rational numbers are there between two rational numbers?
Between any two given rational numbers there are infinitely many rational numbers.
Which rational number is multiplicative identity for all rational numbers.
One (1) is the multiplicative identity for rational numbers.
About Preparation of Class 8 Maths Chapter 1
Commutative and associative rules students will have to apply in other lessons also, so learn it well. It should also be known to find the additive inverse and multiplicative inverse of different rational numbers. Students can contact anytime for any problem related to the study. There is no need to hesitate. Our main purpose is your help. Before starting this chapter, students should know about Natural Numbers, Whole Numbers, Integers (Positive and Negative), etc so that they can understand each and every term properly.
NCERT (https://ncert.nic.in/) Textbook Solutions for Class 8 other subjects are also available in PDF format. Class 8 Maths Chapter 1 Rational Numbers Sols are given in updated form for 2024-25 to use online as well as download in PDF format. If you face any problem during download, please call us, we will immediately solve the problem.
Associative Property of Integers
| Operation | Numbers | Remarks |
|---|---|---|
| Addition | Is (–2) + [3 + (– 4)] = [(–2) + 3)] + (– 4)? Is (– 6) + [(– 4) + (–5)] = [(– 6) +(– 4)] + (–5)? For any three integers a, b and c, we have a + (b + c) = (a + b) + c | Addition is associative |
| Subtraction | Is 5 – (7 – 3) = (5 – 7) – 3? No. | Subtraction is not associative |
| Multiplication | Is 5 × [(–7) × (– 8) = [5 × (–7)] × (– 8)? Is (– 4) × [(– 8) × (–5)] = [(– 4) × (– 8)] × (–5)? For any three integers a, b and c, we have a × (b × c) = (a × b) × c | Multiplication is associative |
| Division | Is [(–10) ÷ 2] ÷ (–5) = (–10) ÷ [2 ÷ (– 5)]? No | Division is not associative |