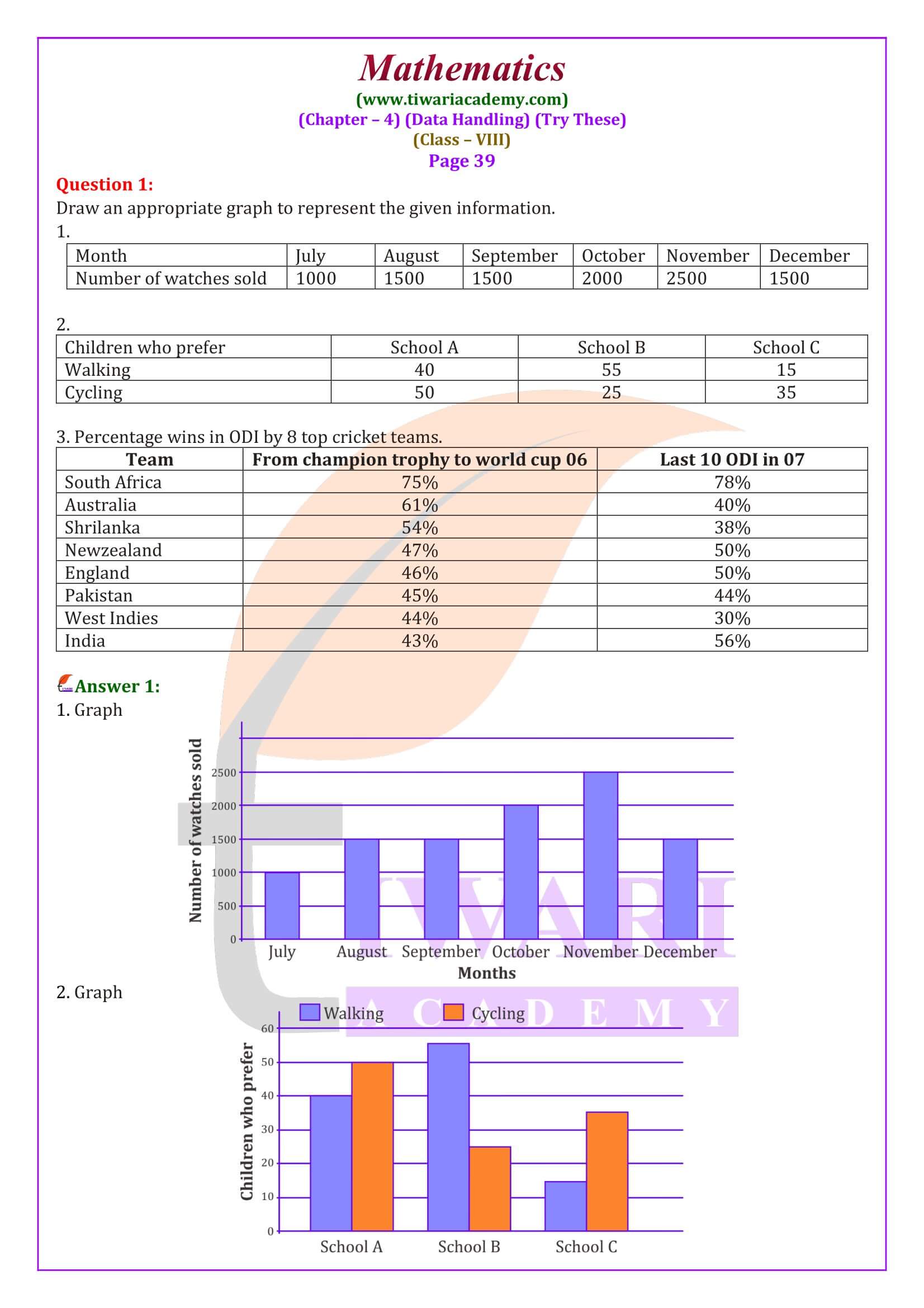
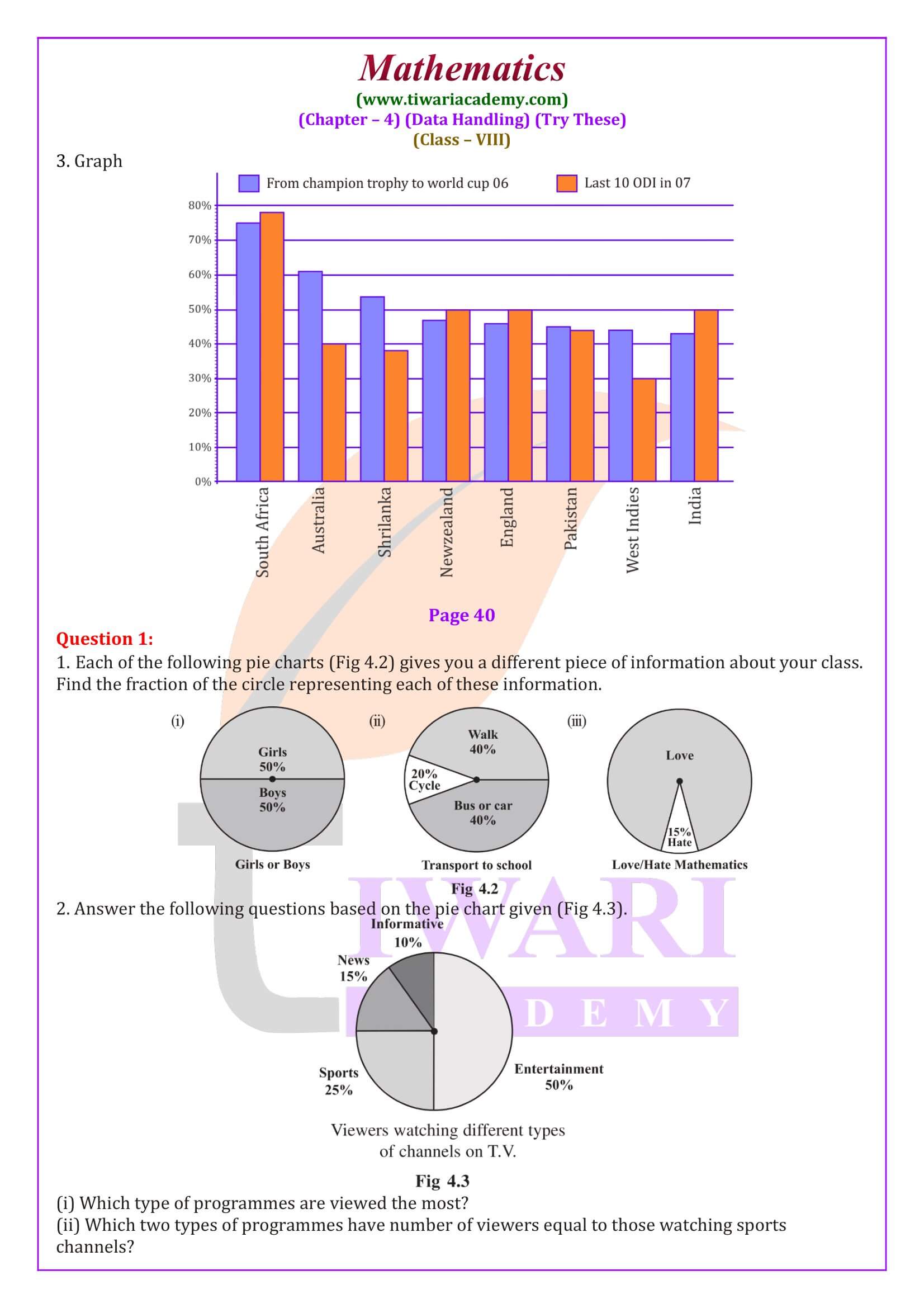
NCERT Textbook Solutions for Class 8 Maths Chapter 4 Data Handling and Class 8 Maths Chapter 4 Try These solutions in Hindi and English Medium for Session 2025-26. According to new revised syllabus and latest NCERT books for academic year 2025-26, there are only two exercises in 8th Maths chapter 4 Data Handling. Data handling is a critical chapter in the NCERT Class 8 Mathematics syllabus, providing students with the tools to interpret, analyze and represent data. NCERT Textbook Solutions for Class 8th Maths Chapter 4 Data Handling are invaluable resources for understanding concepts such as bar graphs, pie charts and probability.
NCERT Exercise Solutions for Class 8 Maths Chapter 4
NCERT 8th Math chapter 4 covers important exercises like Class 8 Mathematics Chapter 4 Exercise 4.1 Solutions, ensuring students grasp basic concepts effectively. The solutions for Class 8 Mathematics NCERT Exercise Chapter 4 PDF download make learning convenient for students, enabling them to revise anytime. NCERT Assignment Class 8 Maths Chapter 4 answers are meticulously designed to match CBSE standards, making Data Handling Chapter 4 NCERT Best Prepared Solutions reliable and easy to comprehend. For further clarity, the Class 8 Math NCERT Book Chapter 4 Notes are a great way to prepare for exams, ensuring students excel in Data Handling.
8th Maths Chapter 4 ncert solutions for CBSE Board
8th Maths Chapter 4 Solutions for State Boards
Importance of NCERT Solutions for Chapter 4
NCERT Detailed Solutions for Class 8 Mathematics Chapter 4 provide step-by-step explanations, helping students solve challenging problems in the Data Handling chapter. NCERT Class 8th Math Chapter 4 solutions, available as a Class 8 Mathematics Exercise Chapter 4 PDF download, ensure accuracy and adherence to the CBSE syllabus. For instance, solving Data Handling Class 8 Math Exercise 4.2 Solutions equips students with the skills to tackle probability-related questions effectively.
The Data Handling Class 8 NCERT Mathematics Important Questions included in the solutions are ideal for practice and exam preparation. With the help of Class 8 Math Exercise NCERT Chapter 4 Exercise Solutions, students can approach topics like bar graphs and pie charts with confidence. For those looking for additional support, NCERT Textbook Class 8 Maths Chapter 4 Assignment, Worksheet and practice materials are highly recommended, making the learning process smoother and more enjoyable.
8th Maths Chapter 4 Solutions in Hindi Medium
Effective Practice for Data Handling
To master Data Handling of Maths section, consistent practice with resources like NCERT Textbook Solutions for Class 8 Mathematics Chapter 4 is crucial. NCERT 8th Maths Chapter 4 solutions not only help with Class 8th Maths Exercises Chapter 4 Practice Questions but also provide detailed guidance on how to approach problems methodically. With the availability of NCERT Math Exercise Class 8 Chapter 4 Solutions in a downloadable PDF format, students have the flexibility to study on-the-go.
Class 8 Maths NCERT Book Chapter 4 Important Questions and worksheets ensure comprehensive revision of topics such as mean, median and mode. The Data Handling NCERT Class 8 Mathematics Solutions are structured to enhance problem-solving skills and build conceptual clarity. By using Class 8 Math Textbook Chapter 4 Notes alongside the NCERT best explained solutions, students can thoroughly prepare for their exams, making this chapter a scoring opportunity in the CBSE Class 8 syllabus.
Important Points in Class 8 Maths Chapter 4 for Final Exams
Data Representation: Learn bar graphs, pie charts and frequency tables.
Measures of Central Tendency: Understand mean, median and mode calculations.
Probability Basics: Grasp simple probability concepts.
Practice Exercises: Focus on Class 8 Maths Chapter 4 Exercise Solutions.
Applications: Solve real-life data problems to enhance understanding.
| Day | Topic | Resources | Practice |
|---|---|---|---|
| Day 1 | Introduction to Data Handling | NCERT Chapter PDF | Read examples and definitions |
| Day 2 | Bar Graphs and Pie Charts | Class 8 Maths Notes | Solve Exercise 4.1 |
| Day 3 | Probability Basics | Important Questions | Practice Exercise 4.2 |
| Day 4 | Revision and Doubts | Worksheets | Mock Tests |
NCERT Solutions for Class 8 Maths Chapter 4
Class VIII Maths Exercise 4.1 and Exercise 4.2 in English Medium as well as Hindi Medium updated for new academic session for new NCERT Books. Download Prashnavali 4.1 and Prashnavali 4.2 in Hindi Medium to study online or download in PDF file format free. All the NCERT textbook solutions are updated as per new CBSE Syllabus for 2025-26. Download NCERT Books and offline apps to use it online or offline.
| Class: 8 | Mathematics |
| Chapter 4: | Data Handling |
| Number of Exercises: | 2 |
| Content: | Textbook Exercises Solution |
| Content Mode: | Text and Videos Format |
| Academic Session: | Year 2025-26 |
| Medium: | English and Hindi Mediun |

Class 8 Maths Chapter 4 Solutions
Class 8 Maths Chapter 4 Data Handling all exercises question answers in Video Format English Medium as well as Hindi Medium are given to study online or download in PDF form. Download Class 8 Maths App for offline use. It works without internet, once downloaded.

Important Terms about Class 8 Maths Chapter 4
What will be total outcomes tossing two coins together?
When two coins are tossed together. There are four possible outcomes HH, HT, TH, TT.
(Here HT means head on first coin and tail on second coin and so on.)
Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of getting a number 6?
Outcome of getting a number 6 from 10 separate slips is one.
Therefore, probability of getting a number 6 = 1/10
In chapter 4 Data handling, we will learn the concepts about Grouped and Raw Data, the Frequency of data in a particular survey, Drawing of Bar graph and Histogram taking proper scale on axis. How to draw a Pie Chart or Circle Chart converting all the given grouped data into angles or percentages. Class 8 Mathematics chapter 4 also give a brief information about the concepts of Probability and the questions based on daily life related to probability. Before doing the questions on probabilities, we should go through the following points:
1. One or more outcomes of an experiment makes an EVENT.
2. Probability of an event can’t be more than 1.
3. Probability of an event can’t be less than 0.
Do you know?
When there is only one coincidence of the result in each experiment, the result is called even potential or isomeric. The probability of any event can never be less than 0 and not more than 1. Thus the probability of any event lies in 0 ≤ p (x) ≤ 1.
If there is any error in the given solution, please inform us and we will try to fix it within 24 hours.
Download NCERT Books and Offline apps based on new CBSE Syllabus. Ask your doubts and share your knowledge with your friends and other users using Discussion Forum. Always feel free to contact us for any educational help.
What is the importance of NCERT Solutions for Class 8 Maths Chapter 4 Data Handling?
NCERT Exercise Solutions for Class 8 Mathematics Chapter 4 Data Handling are essential for understanding concepts such as bar graphs, pie charts and probability. NCERT Class 8th Maths solutions provide step-by-step explanations, making it easier for students to tackle Class 8 Math Textbook Chapter 4 Exercise Solutions. The solutions align with the CBSE syllabus, ensuring students are well-prepared for exams. The Data Handling Class 8 Maths Book Solutions help in building a strong foundation in data interpretation. With resources like the Class 8 Maths Chapter 4 Notes and worksheets, students can practice effectively and enhance their problem-solving skills for better academic performance.
How can I access Class 8 Maths Chapter 4 PDF download for study?
Students can easily access the NCERT Class 8 Mathematics Chapter 4 PDF download from trusted educational websites or apps like Tiwari Academy Learning App. This resource is ideal for revising important topics like mean, median, and mode. The downloadable format allows students to study Data Handling Class 8 Exercise Solutions offline. The Class 8 Math Book Chapter 4 Important Questions included in the PDF help students practice exam-relevant problems. These resources also include solutions for Class 8 Maths Chapter 4 Exercise 4.1 and 4.2, ensuring comprehensive coverage of the chapter. Using these PDFs is a convenient way to prepare thoroughly for exams.
What topics are covered in NCERT Solutions for Data Handling Class 8?
NCERT Detailed Solutions for Class 8 Maths Chapter 4 cover a wide range of topics, including data representation using bar graphs, pie charts and frequency tables. The chapter 4 of 8th Mathematics also introduces students to concepts like mean, median, mode and probability. Detailed explanations in the solutions make Class 8 Maths Chapter 4 Exercise 4.2 Solutions easy to follow. Data Handling Class 8 Maths Solutions include examples and practice questions to strengthen understanding. The Class 8 Maths Chapter 4 Notes and worksheets complement the solutions, ensuring students are well-equipped to solve Data Handling Class 8 Important Questions with confidence.
How do Class 8 Maths Chapter 4 Exercise Solutions help in exam preparation?
Class 8 Maths Chapter 4 Exercise Solutions play a significant role in exam preparation by providing detailed answers to every question in the Data Handling chapter. These solutions cover exercises like Class 8 Maths Chapter 4 Exercise 4.1 Solutions and Mathematics Textbook Exercise 4.2 Solutions, helping students develop a step-by-step approach to problem-solving. The inclusion of Data Handling Class 8 Important Questions ensures students are exposed to various question types that may appear in exams. NCERT Class 8 Chapter 4 Solutions and worksheets make it easier to revise and practice key topics, enabling students to perform confidently in their exams.
Why is regular practice important for mastering Data Handling in Class 8 Maths?
Regular practice is crucial for mastering the Data Handling chapter as it helps students build confidence and improve their analytical skills. NCERT Solutions for Class 8 Maths Chapter 4 provide a reliable resource for practicing Class 8 Maths Chapter 4 Practice Questions. These solutions include a Class 8 Maths Chapter 4 PDF download, allowing students to access important materials anytime. Worksheets, notes and Data Handling Class 8 Maths Solutions make it easier to understand concepts like mean, median and mode. By solving Class 8 Maths Chapter 4 Exercise Solutions regularly, students can strengthen their foundation and excel in exams.