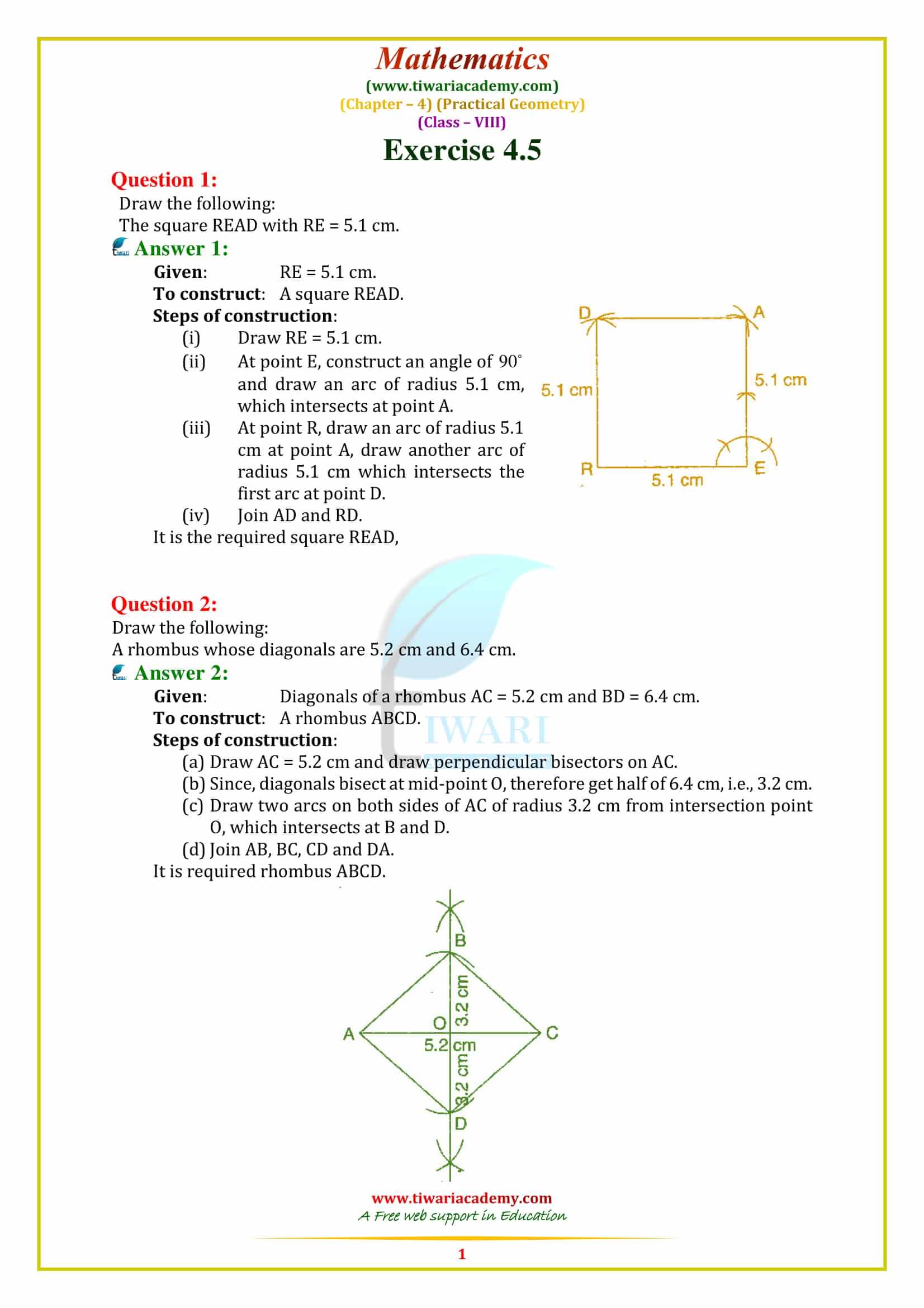
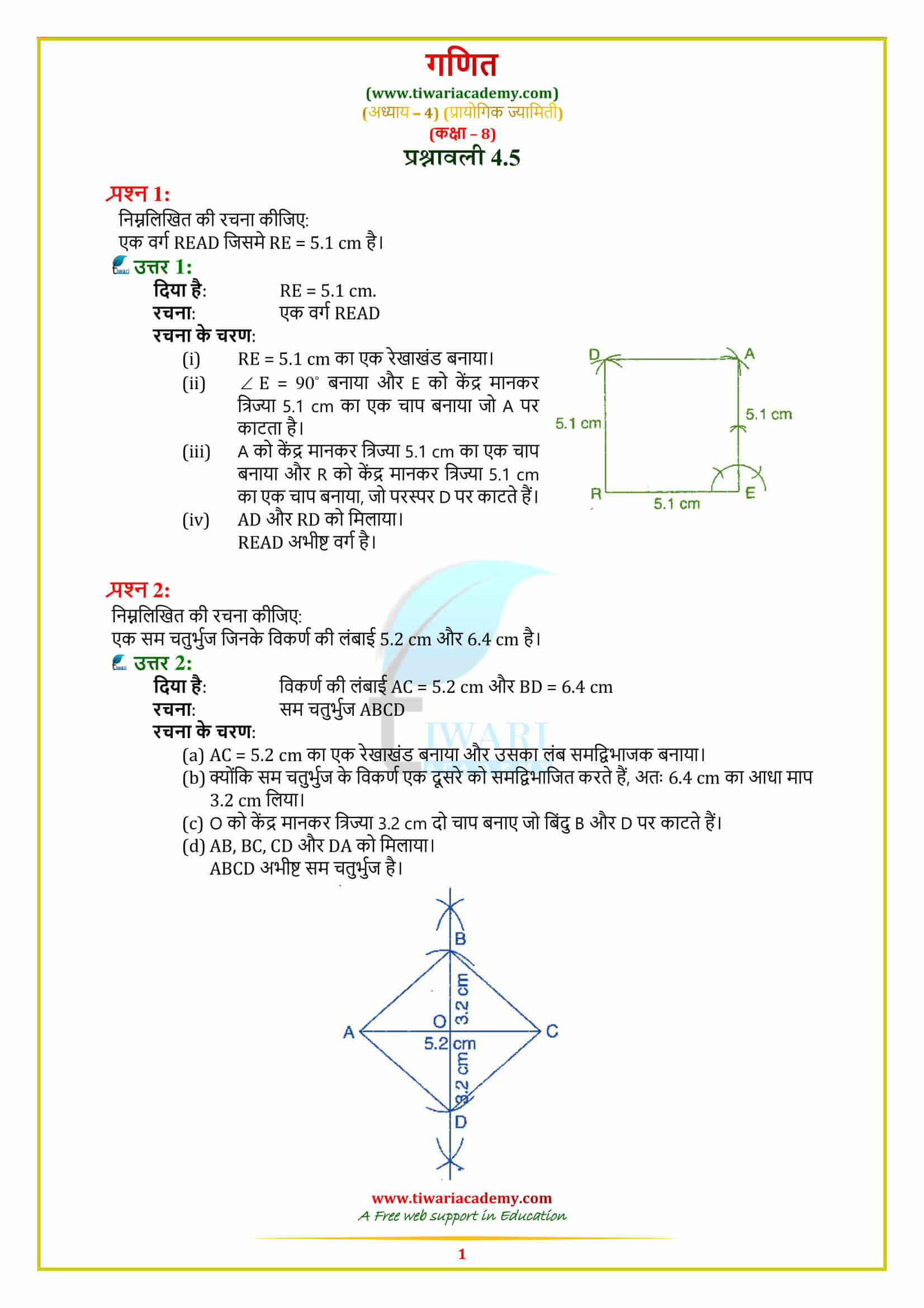
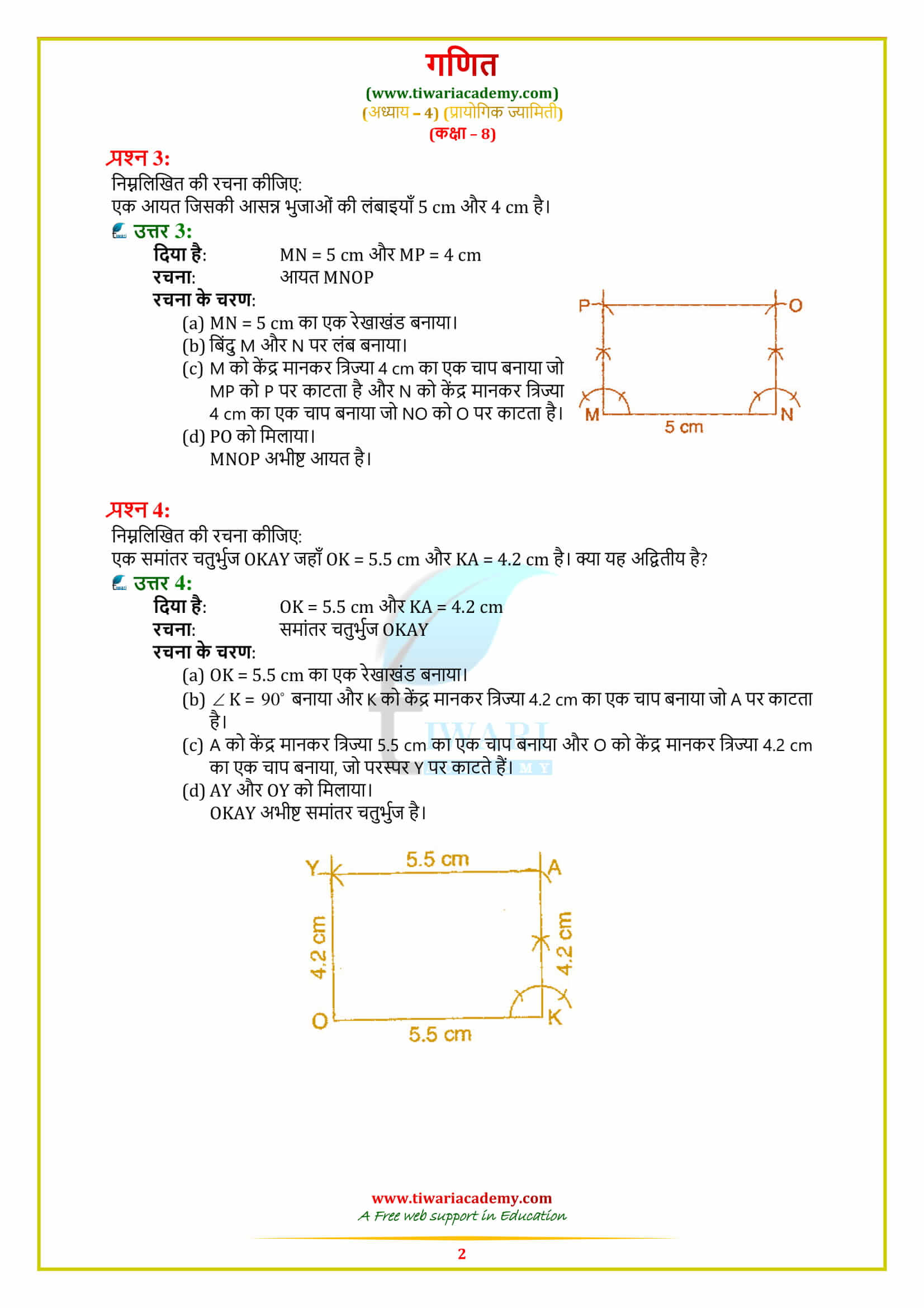
NCERT Solutions for Class 8 Maths Chapter 4 Exercise 4.5 Practical Geometry in Hindi and English Medium updated for CBSE new session. Unlock comprehensive NCERT solutions for Class 8 Maths Chapter 4, Exercise 4.5 on Practical Geometry, now available in Hindi and English. Perfectly tailored for CBSE and State board curricula, Tiwari Academy provides these updated resources for free to enhance your learning experience.
8th Maths Exercise 4.5 Solution in Hindi and English Medium
Class 8 Maths Chapter 4 Exercise 4.5 Solution
Class VIII Mathematics NCERT Ex. 4.5 Practical Geometry updated for CBSE academic session 2024-25 free to download or use online. All the contents are free to use without any login or password. All the constructions given in ex. 4.5 of class 8 mathematics are solved here step by step using easier methods. Videos related to 8th NCERT Maths exercise 4.5 is also given with the PDF solutions.
| Class: 8 | Mathematics |
| Chapter: 4 | Exercise: 4.5 |
| Topic Name: | Practical Geometry |
| Medium: | Hindi and English |
| Content Mode: | Text and Videos |
To Construct a Quadrilateral When 4 Sides and One Angle Are Given:
Construct a quadrilateral ABCD in which AB = 3.8 cm. BC = 3.4 cm, CD = 4.5, cm AD = 5 cm and ∠B = 80°. Steps of construction:
First we draw a rough sketch of quad. ABCD and write down its dimensions as given.
Step 1. Draw AB = 3.8 cm
Step 2. Make ∠ABX = 80°
Step 3. From B. set off BC = 3.4 cm.
Step 4. With A as centre and radius equal to 5 cm, draw an arc.
Step 5. With C as centre and radius equal to 4. 5 cm, draw another arc, cutting the previous arc at D. Step 6. Join AD and CD.
Then, ABCD is the required quadrilateral.
How do you know if 4 points form a quadrilateral?
A quadrilateral formed by the points A, B, C and D is complex, if the intersection of AB and CD (if any) lies between the points A and B, and the same applies for BC and DA.
Class 8 Maths Exercise 4.5 Important Questions
Draw a trapezium ABCD in which AB || DC, AB = 5 cm, AD = BC = 6.5 cm and ∠B = 60°.
Construct a quadrilateral ABCD in which AB || DC, AB = 5 cm, AD = BC = 6.5 cm and ∠B = 60°.
Steps of construction:
First we draw a rough sketch of quad. ABCD and write down its dimensions as given.
Step 1. Draw AB = 5 cm
Step 2. Make ∠ABX = 60°
(∠C = 1800 – 600 = 1200 because ∠C is supplementary angle of corresponding angle of ∠B)
Step 3. Make ∠BCZ = 120°
Step 4. With C as centre and radius equal to 6.5 cm, draw an arc cutting CZ at point D.
Step 6. Join AD
Then, ABCD is the required quadrilateral,
Construction of Special Types of Quadrilaterals
Construct a parallelogram ABCD in which AB = 6 cm, BC = 4.5 cm and diagonal AC = 6.8 cm.
Draw a rough sketch of the required parallelogram and write down the given dimensions.
Steps of construction:
(i) Draw AB = 6 cm.
(ii) With A as centre and radius 6.8 cm draw an arc.
(iii) With B as centre and radius 4.5 cm draw another arc, cutting the previous arc at C.
(iv) Join BC and AC.
(v) With A as centre and radius 4.5 cm, draw an arc.
(vi) With C as centre and radius 6 cm draw another arc, cutting the previously drawn arc at D.
(vii) Jon DA and DC.
Then, ABCD is the required parallelogram.
Construct a parallelogram, one of whose sides is 5.2 cm and whose diagonals are 6 cm and 6.4 cm.
We know that the diagonals of a parallelogram bisect each other.
Make a rough sketch of the required parallelogram, as shown.
Steps of construction:
(i) Draw AB = 5.2 cm.
(ii) With A as centre and radius 3.2 cm, draw an arc.
(iii) With B as centre and radius 3 cm draw another arc, cutting the previous arc at O.
(iv) Join OA and OB.
(v) Produce AO to C such that OC = AO and produce BO to D such that OD = OB.
(vi) Join AD, BC and CD.
Then, ABCD is the required parallelogram,
How many set squares are needed to make a quadrilateral?
Thus a quadrilateral has 10 elements (4 sides, 4 angles and 2 diagonals) or measurements. To construct a unique quadrilateral, we need to know 5 measurements (elements).
Note:
To construct a unique quadrilateral simply the knowledge of any five elements is not sufficient.
How many sides does a regular polygon have if the measure of an exterior angle is 24 degrees?
Since the sum of the exterior angles is always 360 degrees, if you divide 360 degrees by 24 degrees you get 15 which is the number of equal exterior angles and therefore 15 vertices and sides to the polygon.